И характеристика видов трения

 

Триботехника – это упорядоченные знания о практическом применении трибологии – науке о трении и процессах, сопровождающих трение (от греческих слов «трибос» - трение и «логос» - наука) [143].

Предметом изучения триботехники являются процессы, протекающие в узлах трения машин и механизмов при их работе, методы повышения надежности узлов трения.

Появление и становление триботехники как прикладной науки обусловлены следующими причинами [143]:

§ огромные затраты энергии на преодоление трения. Сопротивление трения поглощает во всем мире 30…40% вырабатываемой энергии;

§ нагрев узлов машин в результате диссипации энергии трения приводит их к интенсивному износу и поломке. Примерно 80…90% отказов узлов машин происходит из-за их износа;

§ большие потери средств в машиностроении вследствие износа деталей. Для промышленно развитых стран они составляют 4…5% национального дохода;

§ большие затраты материальных средств для уменьшения трения. За год в мире расходуется более 100 млн. тонн смазочных материалов;

§ огромное отвлечение людских и материальных ресурсов на ремонт изношенных деталей (около 30% рабочих и станочного парка, около 20% выплавляемого металла).

Трение возникает, когда два тела перемещающихся относительно друг друга, соприкасаются своими внешними поверхностями (внешнее трение) или когда элементы структуры тела (атомы, молекулы) перемещаются относительно друг друга (внутреннее трение).

Энергия трения (работа, совершаемая на преодоление сил трения) частично диссипируется (рассеивается) в тепловую энергию, которая приводит к нагреву узлов трения. Другая часть энергии трения расходуется на деформацию деталей, отделение частиц материала с поверхности трения и ее пластическую деформацию, то есть на износ. Третья часть энергии может быть причиной фазовых переходов окислов металлов, может выделяться в виде электромагнитных и звуковых излучений и тому подобное.

Трение – комплекс явлений в зоне контакта поверхностей двух перемещающихся относительно друг друга тел, в результате чего в этой зоне возникают контактные силы [56].

Внутренне трение в первую очередь появляется в жидкостях и газах, обладающих легкой подвижностью. Например, движение жидкости между двумя перемещающими относительно друг друга пластинами А и Б (рис. 2.15). Силовой характеристикой внутреннего трения является сила трения, определяемая по закону Ньютона

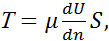(2.19)

где – градиент скорости частиц жидкости; S – площадь пластин; μ - коэффициент динамической вязкости жидкости.

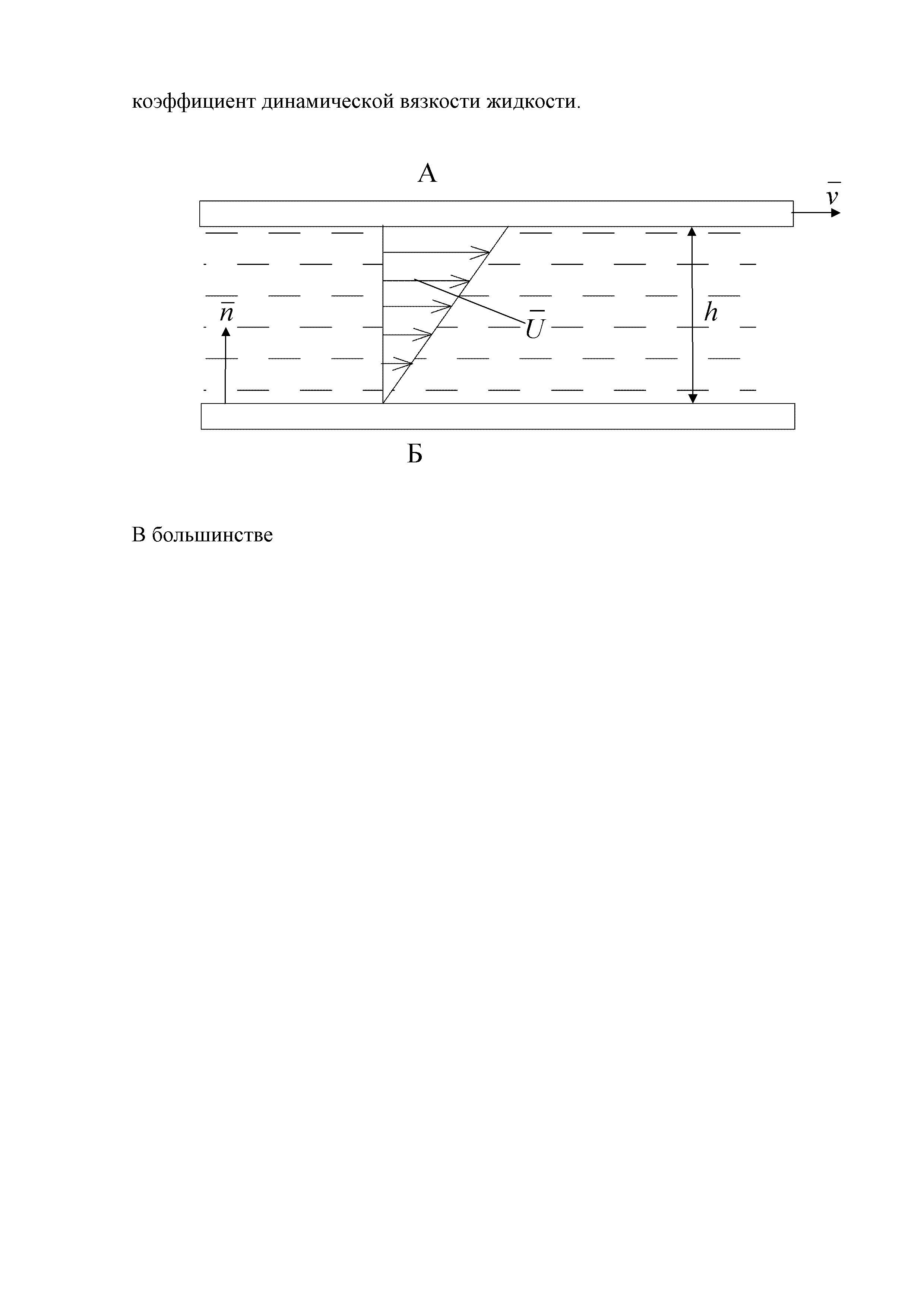
Рис. 2.15. Внутреннее трение в жидкости 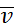- скорость относительного движения пластин; 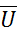- скорость частиц жидкости; h - толщина слоя жидкости; - нормаль к поверхности пластины

 

Внешнее трение – процесс диссипации энергии, протекающий при относительном тангенциальном перемещении соприкасающихся твердых тел, осуществляемом в зонах реального контакта этих тел, образовавшихся под действием внешней нагрузки [143].

Классификация видов трения по различным признакам приведена на рис. 2.16. По характеру движения различают трение скольжения и качения (рис. 2.17)

Признаки классификации

Трение

Внутреннее (одно)

Внешнее (несколько)

Движения

Наличие движения

Покоя

Качения

Скольжения

Характер движения

Без смазочного материала

Со смазочным материалом

Наличие смазочного материала

Количество тел трения

 

Рис. 2.16. Классификация видов трения

 

Сила трения является количественной оценкой трения и представляет собой равнодействующую сил тангенциальных сопротивлений, возникающих на реальных пятнах контакта при скольжении одного тела по поверхности другого. Сила трения – не потенциальная сила.

 

 

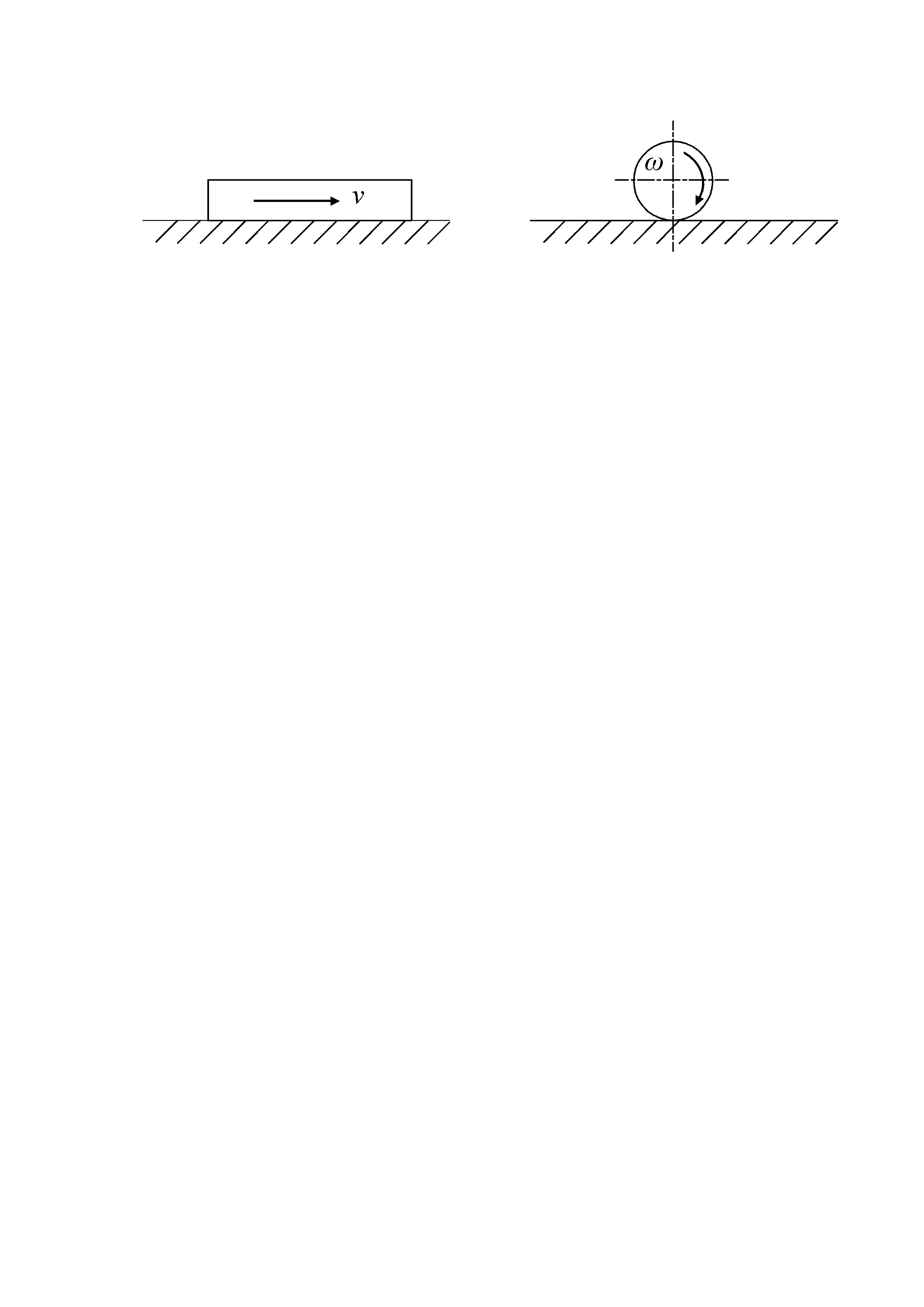
Рис. 2.17. Виды внешнего трения по характеру движения

 

При переходе от покоя к скольжению имеется участок предварительного смещения рис. 2.18. После того, как сила, действующая на тело, превысит силу трения покоя Т_А, произойдет срыв и начнется устойчивое скольжение тела, при этом сила трения Т_В < Т_А.

Краткая историческая справка.

В 1692 году Амонтон открыл закон внешнего трения:

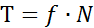, (2.20)

где f - коэффициент внешнего трения, f не зависит от нагрузки N.

Рис. 2.18. Зависимость силы трения Т от величины смещения х:

0х₁ - предварительное смещение х₁ х₂ – срыв; Т_А – полная сила трения (трение покоя); Т_В – сила трения скольжения

 

В 1778 году Шарль-Огюст Кулон предложил двучленную формулу для внешнего трения:

, (2.21)

где А – характеристика сцепленности двух тел, А не зависит от внешней нагрузки.

С появлением учения о молекулярном строении веществ (М.В. Ломоносов, 1711-1765 г.) развитие теории трения получило новый толчок. В 1934 г. Дерягин Б.В. раскрыл физическую суть двучленного закона трения, доказав, что молекулярные силы притяжения определяют сцепленность тел при внешнем трении, и записал закон в таком виде [56]:

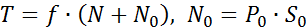, (2.22)

где N₀ - равнодействующая сил молекулярного притяжения между трущимися поверхностями; P₀ - сила молекулярного притяжения; S₀ - площадь контакта, на который действует молекулярные силы притяжения (площадь фактического контакта).

Дальнейшее развитие теории внешнего трения было дано в трудах И.В. Крагельского, а теория получила название молекулярно-механической, в которой природа внешнего трения считается двойственно (адгезия + деформация).

Режимы трения. В зависимости от наличия и количества смазочного материала между поверхностями трения различают сухой, граничный, полужидкостный и жидкостные режимы трения (рис. 2.19).

Рис. 2.19. Схемы режимов трения: а – жидкостный; б – полужидкостный;

в – граничный; г – сухой (1, 2 – поверхности трения,

3 – смазочный материал, 4 – граничный слой смазки)

Жидкостный режим трения характеризуется тем, что поверхности трения полностью разделены слоем жидкой смазки и реализуется только внутреннее трение жидкости. При этом износ отсутствует.

Полужидкостной режим трения характеризуется тем, что происходит соударение отдельных выступов микронеровностей, коэффициент трения возрастает, все пространство между поверхностями трения заполнено жидкой смазкой. При работе на этом режиме происходит износ поверхностей трения, но его интенсивность незначительна.

Для граничного трения характерно то, что на поверхностях, соприкасающихся своими микровыступами, присутствует смазочный материал в виде граничного слоя квазикристаллической структуры (адсорбированных и ориентированных вертикально молекул смазки), а пространство между граничными слоями заполнено воздухом или газом. Граничный слой выдерживает без разрушения огромные нормальные напряжения и практически не сопротивляется касательным усилиям. Интенсивность изнашивания и коэффициент трения больше, чем у полужидкостного.

Коэффициент трения f правильно рассчитанных и работающих в условиях жидкостной смазки подшипников скольжения равен 0,001-0,005. Однако при неблагоприятных условиях (высокая вязкость масла, большие окружные скорости, малые зазоры) коэффициент трения возрастает до 0,01-0,03. У подшипников, работающих при граничной смазке, коэффициент трения f достигает значений 0,1- 0,2 [129].

Тяжело нагруженные и работающие при высокой частоте вращения подшипники нуждаются в непрерывном подводе масла под давлением для поддержания режима жидкостной смазки и отвода теплоты, выделяющейся при трении. Подшипники скольжения надежно работают при температуре не выше 150⁰С. При более высокой температуре возникает опасность разрыва масляного слоя вследствие разжижения масла и быстрого окисления и потери смазочных свойств.

В подшипниках скольжения встречаются три основных вида смазки: жидкостная, полужидкостная и граничная. При жидкостной смазке поверхности вала и подшипника разделены сплошным масляным слоем, непосредственное трение между металлическими поверхностями вала и подшипника отсутствует. Коэффициент трения при жидкостной смазке незначителен (f = 0,001); потери на трение и тепловыделение в подшипнике невелики.

Обязательным условием жидкостной смазки является обильная непрерывная подача масла в подшипник. Давления в масляном слое, необходимые для несения действующих на подшипник нагрузок и предупреждения контакта между поверхностями, создаются при эксцентричном положении вала в подшипнике в результате непрерывного нагнетания вращающимся валом масла в суживающуюся часть зазора. Этот самоподдерживающий процесс носит название гидродинамической смазки [129]. Вал, установленный в подшипнике с диаметральным зазором S, под действием постоянной нагрузки Р занимает эксцентричное положение (рис. 2.20).

Рис. 2.20. Распределение давления внутри масляного слоя

 

А – в продольном сечении; Б – в поперечном сечении; Р – нагрузка, 1 – местное давление внутри масляного слоя, х-х – эпюра давлений, внутри масляного слоя, у – область разряжения.

По обе стороны от точки наибольшего сближения вала и подшипника зазор принимает форму клиновидной щели. Вращаясь, вал увлекает с собой масло. Первый слой масла, смачивающий вал, увлекает вследствие адсорбции масла металлической поверхностью вала, последующие слои – вследствие внутренней вязкости масла. Вал, таким образом, действует как насос, нагнетающий масло в клиновидную щель.

Максимальное давление на участке наибольшего сближения вала и подшипника примерно в 2-3 раза превышает среднее давление [129]

, (2.23)

где d- диаметр; l- длина подшипника, Р - сила, действующая на подшипник.

В области жидкостной смазки положение центра вала определяется параметром

, (2.24)

где η- динамическая вязкость масла, ω - угловая скорость, - среднее давление.

Относительная толщина масляного слоя 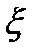это отношение минимальной толщины h_min масляного слоя в точке наибольшего сближения вала и подшипника к радиальному зазору :

, (2.25)

так как , где е – эксцентриситет, то

, (2.26)

Относительный эксцентриситет и относительная минимальная толщина масляного слоя являются функцией безразмерного числа Зоммерфельда [129]:

(2.27)

и отношения l/d длины подшипника к диаметру, где η - динамическая вязкость масла, ; ω - угловая скорость, рад/с; – среднее давление, Па; ψ - относительный зазор (ψ = S/d).

Зная (по известным η, ω, Р, ψ,) величину S₀, можно найти значение для данного отношения l/d и определить минимальную толщину масляного слоя (в мкм) из выражения [129]

, (2.28)

среднее давление на подшипники, обратно пропорционально величине S₀ и определяется [129]

. (2.29)

Для практических целей удобнее пользоваться характеристикой режима (2.24).

Так как , то величины 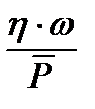и связаны соотношениями:

, . (2.30)

Критической характеристикой режима называют значение λ, при котором минимальная толщина масляного слоя уменьшается постоянно, что наступает соприкосновение микронеровностей вала и подшипника, и коэффициент трения резко возрастает. Толщину масляного слоя, при которой возникает полужидкостная смазка, называют критической и обозначают h_кр. Величина h_кр для хорошо выполненных гладких и жестких подшипников и валов составляет в среднем 5-10 мкм [129].

Коэффициентом надежности подшипника называют отношение рабочей характеристики режима к критической [129], которое должно быть больше единицы

> 1 . (2.31)

Чем больше , тем меньше опасность перехода работы подшипника в область полужидкостной смазки.

Окружная сила Т, противодействующая вращению вала, равна сумме сил вязкого сдвига масла в зазоре по всей окружности вала. По закону вязкого трения Ньютона при ламинарном течении сила Т пропорциональна поверхности сдвига (то есть величине π·d·l) вязкости масла η, скорости сдвига υ и обратно пропорциональна толщине h масляного слоя [129].

При концентричном расположении вала h=0,5 ,

Следовательно:

, (2.32)

коэффициент трения при жидкостной смазке [129] (формула Н.П.Петрова)

. (2.33)

Подставляя в формулу (2.33) значение 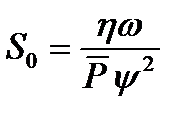, получаем .

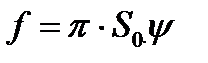При эксцентричном расположении вал (S₀ <1) коэффициент трения определяют по формуле Г. Фогельполя [129]

. (2.34)

Большие зазоры неблагоприятны для несущей способности, но способствуют уменьшению трения и увеличению прокачки масла. Рабочая температура подшипников с большим зазором меньше; повышенная благодаря этому вязкость масла компенсирует их малую несущую способность. Этим объясняется способность подшипников скольжения работать даже при довольно больших износах.

Подшипники с малым зазором вследствие повышенного тепловыделения работают при высокой температуре; однако пониженная вязкость масла компенсируется свойственной этим подшипникам высокой нагруженностью. Аналогичную способность саморегулирования подшипник проявляет и при колебаниях рабочего режима.

Таким образом, фактор η играет роль регулятора, который стремится при изменении характеристики режима восстановить ее первоначальное значение. Главное условие заключается в том, чтобы механизм восстановления равновесия мог действовать во всем диапазоне возможных колебаний режима, без перехода опасных значений h_{mi n}. Для этого нужно, чтобы подшипник был рассчитан с достаточным коэффициентом надежности и работал в области достаточно больших эксцентриситетов.

Количество энергии (теплоты), выделяющейся в подшипнике за единицу времени (Вт) [129]

, (2.35)

где P – нагрузка на подшипники, Н; υ - окружная скорость, м/с.

Количество теплоты, уносимой маслом из подшипника за единицу времени [129]

, (2.36)

где Q – объем масла, вытекающего из подшипника за единицу времени, м³/с; - плотность масла, кг/м³; с – удельная теплоемкость масла, Дж/(кг · град); Δt = t_вых – t_вх - повышение температуры в подшипнике; t_вх и t_вых – температура масла на входе и выходе из подшипника.

В состоянии теплового равновесия R=R′:

, (2.37)

откуда . (2.38)

Плотность минеральных смазочных масел в диапазоне 20-100⁰С колеблется в пределах кг/м³, удельная теплоемкость (1,8¸2,3)10³ Дж/(кг град).

Подставляя эти значения в формулу Δt, получаем [129]

. (2.39)

Объем масла, м³/с, вытекающего из подшипника, по Г.Фогельполю [129]:

, (2.40)

где р – давление подачи масла, Па.

Подставляя Q в уравнение Δt (2.99), после преобразований получаем:

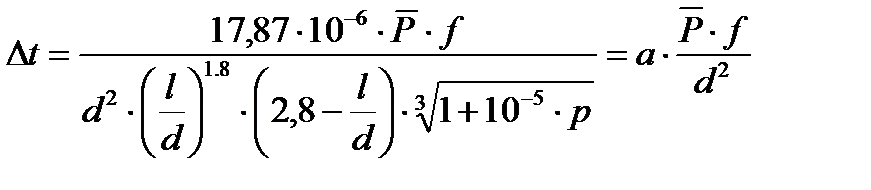. (2.41)

Отсюда видно, что при заданной нагрузке повышение температуры в подшипнике обратно пропорционально квадрату диаметра и прямо пропорционально f ифактору а:

. (2.42)

Для проектировочного расчета подшипника с оптимальным значением ξ =0,3 надо знать и n, задаться значением d, l/d, давлением р и температурой t_вх подачи смазочного масла, а также его сортом.

При расчете подшипников из бронзы, алюминиевых сплавов решающим являются гидродинамика подшипника, его геометрические (d, l/d, ψ) и режимные (λ) факторы, рациональный выбор которых позволяет довести удельные нагрузки до 15-30 МПа, а в отдельных случаях до 50-60 МПа [129].

Перегрев подшипника, чрезмерный износ, растрескивание, расплавление и наволакивание материала подшипника на вал, и другие явления неудовлетворительной работы подшипника почти всегда происходят в результате перехода (общего или местного) за критическую толщину масляного слоя и возникновения в подшипнике полужидкостной или граничной смазки. Нередко они бывают следствием недостаточно высоких расчетных значений h_min и λ. В большинстве случаев неполадки обусловлены ошибками конструкции, технологии изготовления и эксплуатации.

Коэффициент полужидкостного трения значительно выше, чем жидкостного (рис. 2.21), тепловыделение в подшипнике больше, поэтому возникновение полужидкостного трения сопряжено с опасностью перегрева и выхода подшипника из строя. Давление вдоль оси в цилиндрическом правильном подшипнике изменяется по кривой параболического типа и резко падает у торцов подшипника в результате истечения масла через торцы (рис. 2.20) [60, 121].

Параболический характер распределения давления по образующей подшипника получил Мичел [121] для так называемого короткого подшипника (R > l/4). Уравнение Рейнольдса для одномерного поперечного сечения имеет следующий вид:

(2.43)

или (2.44)

так как h зависит только от x (x изменяется от 0 до R; θ; - угол отклонения от положения h_min). Интегрируя это уравнение дважды и используя начальные условия р = 0 при у = ± l/2, получаем

(2.45)

где r – радиус шипа (шейки); R – радиус цапфы; С = R – r – средний зазор; υ – скорость скольжения.

Рис. 2.21. Кривая Штрибека и режимы смазки (схема) [195]

 

Эти процессы носят вероятностный характер, что подтверждают эксперименты по относительному времени отсутствия контакта между поверхностями [195, 201]. То есть, снижение давления масла и толщины масляной пленки, повышает вероятность перехода в область граничной смазки (рис. 2.22) с высоким коэффициентом трения.

Количество теплоты, выделяющейся в подшипнике, вследствие повышенного коэффициента полужидкостного трения (f) увеличивается (2.35). Также увеличивается мощность, затрачиваемая на трение [84, 85]

N=P·f·V=P·n ∕ 30·10^-3· d·f ∕ 2 (кВт). (2.46)

Режим сухого трения реализуется для случая отсутствия смазочного материала на поверхности трения. Характеризуется большим значением коэффициента трения и интенсивности изнашивания. Резко возрастает температура узла трения, и появляется вероятность задира, заклинивания или расплавления антифрикционного слоя подшипника.

 

Отношение толщины пленки к шероховатости λ

0,3

f=f(λ)

ζ==ζ(λ)

0,2

0,1

Рис. 2.22. Кривые Штрибека и доли времени отсутствия контакта (схема)

 

Контакт твердых тел происходит на небольших участках поверхности трения, что является следствием наличия на реальных поверхностях шероховатости, волнистости и отклонений формы поверхности от заданной конструктором. На рис. 2.23 приведена топография (а) и профиль по выбранному направлению поверхности образца (б), а на рис. 2.24 приведена топография поверхности трения образца с областью сканирования 3x3 мкм.

 

Рис. 2.23. Топография (а) и профиль по выбранному направлению поверхности образца (б) с областью сканирования 10х10 мкм [80]

Рис. 2.24. Топография поверхности трения образца с областью сканирования 3х3 мкм [80]

 

На рис. 2.25. показана модель контакта твердых тел при трении [143].

а

б

в

Рис. 2.25. Макроскопическое (а), микроскопическое (б) и субмикроскопическое (в) взаимодействие поверхностей

 

При рассмотрении контактного взаимодействия неподвижных поверхностей можно выделить три уровня: макроскопическое, микроскопическое и субмикроскопическое (рис. 2.25).

Геометрические характеристики тел при трении определяют фактическую площадь контакта, следовательно, и напряжения в зоне их взаимодействия и износ.

Форма и размеры твердого тела являются его макрогеометрическими характеристиками. При трении и контакте на износ влияют различные отклонения формы поверхностей: непрямолинейность, некруглость (овальность, огранка), неплоскостность (выпуклость, вогнутость), нециллиндричность (конусообразность, бочкообразность, седлообразность и изогнутость оси), и различные отклонения расположения (несоосность, перекос осей) [ 17, 143].

Микрорельеф определяет дискретность контакта твердых тел и связанные с ним процессы разрушения, а также высокую концентрацию энергии на отдельных участках контакта при трении. Микрорельеф характеризуют волнистостью и шероховатостью.

Совершенно иная картина напряженно-деформированного состояния наблюдается на скользящем контакте трущихся тел при одновременном действии нормальной и тангенциальной сил. При этом образуются фрикционные связи.

Фрикционной связью называют единичное пятно касания, образовавшееся при одновременном действии нормальных и тангенциальных нагрузок и исчезающее при снятии нормальной нагрузки.

Характер нарушения фрикционной связи и комплекс процессов, протекающих на поверхностных слоях и микрообъемах, существенно зависят от ряда факторов: геометрических, механических, физических и химических. Одним из наиболее мощных факторов является геометрический, характеризуемый отношением глубины внедрения к радиусу единичной микронеровности (рис. 2.26).

Величина h/R позволяет различать упругий и пластический контакты, микрорезаюние. Вторым существенным фактором является физико-механический: отношение тангенциальной прочности молекулярной связи к пределу текучести материала основы τ_а/σ_τ.

При этом могут быть реализованы два случая:

- нарушение связи по поверхности раздела двух тел или по пленкам, покрывающим эти тела;

- нарушение связи в глубине основного металла и вырывание.

 

Рис. 2.26. Модель фрикционной связи: 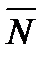- нормальная нагрузка;

- нормальная нагрузка; h – глубина внедрения; R – радиус

 

Принято различать пять видов нарушения фрикционной связи [143] (рис. 2.27).Минимум износа будет реализоваться в случае упругого контакта соприкасающихся микронеровностей, а причина изнашивания – фрикционная усталость.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: