 |
Расчет балки на прочность нормального сечения в середине пролета
|
|
|
|
Расчет балки на прочность нормального сечения в середине пролета по изгибающему моменту выполняется в соответствии с указаниями норм /2/, пп.3,56*, 3,61*, 3,63.
Если Rb b’f h’f ≥ Rs As, то нейтральная ось проходит в пределах высоты плиты и сжатая зона сечения балки имеет прямоугольную форму.
В этом случае высота сжатой зоны бетона х = Rs As / (Rb b’f ).
Прочность нормального сечения проверяют по условию:
M 
(4.33)
Если Rb b’f h’f < Rs As, то нейтральная ось проходит в пределах ребра главной балки (см. Рисунок 4.5) и сжатая зона сечения балки имеет тавровую форму. Высота сжатой зоны бетона
(4.34)
Необходимо, чтобы x = х/h0 ≤ xy = (0,85 – 0,008 Rb) / (1 + 0,0001Rs(4,545 – 0,145Rb)). Здесь Rb и Rs принимают в МПа.
Прочность нормального сечения будет обеспечена, если действующий в нем изгибающий момент не больше того момента, который сечение может выдержать, т. е.:
M 
(4.35)
Рисунок 4.5 – Схема для расчета нормального сечения
Расчет балки на выносливость нормального сечения
В середине пролета
В расчетах на выносливость принимают, что растянутый бетон полностью выключился из работы сечения и все растягивающее усилие воспринимается арматурой (см. Рисунок 4.6). В этом случае наибольшие напряжения в бетоне и арматуре балки определяют по формулам:
(4.36)
где Mf,max – изгибающий момент для расчетов на выносливость (см. формулу (4.24));
hu – расстояние от крайнего ряда растянутой арматуры до сжатой грани.
В результате расчета на выносливость должны быть проверены два условия:
sв = 
; ss = 
, (4.37)
где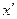 
- высота сжатой зоны;
Ired - приведенный момент инерции;
- отношение модуля упругости арматуры к модулю упругости бетона.
Рисунок 4.6 – Схема для расчета балки на выносливость
|
|
|
Для определения расчетных сопротивлений бетона и арматуры на выносливость необходимо знать максимальные и минимальные значения напряжений в них для определения характеристик цикла повторяющихся напряжений:
ρb = σb,min / σb,max и ρs = σs,min / σs,max;
σb,min = 
; ss,min = 
(4.38)
Здесь возможны два случая: когда Mf,max и Mf,min имеют один или разные знаки. В разрезной балочной системе реализуется первый случай т.е. момент инерции приведенного сечения Ired имеет одно и то же значение, а максимальные и минимальные напряжения как в бетоне, так и в арматуре будут одного и того же знака. Следовательно, ρb = ρs = Mf,min / Mf,max > 0. Для определения Mf,max и Mf,min следует использовать формулу (4.22), предполагая, что минимальное значение изгибающего момента получается при отсутствии временной нагрузки от подвижного состава на пролетном строении.
Значения в нормах принимаются равным: для бетонов классов B20-22,5; В22,5 и В25 – 20; В27,5 – 17; В30 и В35 – 15; В40 и выше – 10.
Остальные нормативные значения расчетных сопротивлений, коэффициенты и формулы для их определения принимаются по Приложению М.
Для изгибаемых элементов произвольного сечения положение нейтральной оси, проходящей через центр тяжести приведенного сечения, может быть определено из условия равенства нулю статического момента всего сечения:
(4.39)
Подставляя в выражение (4.38) значения статических моментов для таврового сечения
; 
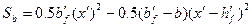(4.40)
и решая полученное уравнение относительно 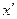, имеем 
,
где 
;
. (4.41)
Приведенный момент инерции сечения при этом
. (4.42)
Расчет балки на трещиностойкость нормального сечения
В середине пролета
В данном разделе выполняются два вида расчета: по образованию продольных трещин и по раскрытию трещин. Напряжения в железобетонных конструкциях с ненапрягаемой арматурой ограничиваются значением расчетного сопротивления Rb, mc2 (см. Приложение М), т.е. должно выполняться условие:
|
|
|
(4.43)
Ширину раскрытия трещин необходимо определить по формуле:
, (4.44)
где σb и σs напряжения в бетоне и арматуре, определяемые по (4.37) и (4.40)-(4.42);
Еs – модуль упругости арматуры (см. Приложение М);
Ψ - коэффициент раскрытия трещин (см. п. 4.1.6 настоящих методических указаний). Следует иметь в виду, что зона взаимодействия должна располагаться в растянутой части сечения, т.е. ее граница не должна выходить за нейтральную ось;
- предельное значение расчетной ширины раскрытия трещин принимается не более 0,020 см (табл. 39* /2/).
|
|
|
