 |
Первый и второй законы Кирхгофа в матричной форме
|
|
|
|
Узловая матрица - это таблица коэффициентов уравнения, составленных по первому закону Кирхгофа. Строки соответствуют узлам, а столбцы - ветвям схемы. Правило знака: если ток в ветви входит в узел, то ставится -1, если ток выходит из узла, то ставится 1, если узел не имеет отношение к данной ветви, то ставится 0.
[A]∙[İ]=[0], где [İ]=[İ1 İ2 İ3 İ4 İ5 İ6]T – столбцовая матрица токов в ветвях;
Контурная матрица – это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа. Строки матрицы соответствуют контурам, а столбцы – ветвям схемы. Правило знака: если ток в ветви совпадает с направлением обхода контура, то ставится 1; если ток в ветви имеет направление, противоположное направлению обхода контура, то ставится -1; если ветвь не входит в контур, то 0. На основании контурной матрицы можно записать уравнение по 2 закону Кирхгофа: [B]∙[Ů]=[0], где [Ů]=[ Ů1 Ů2 Ů3 Ů4 Ů5 Ů6]T – столбцовая матрица напряжений ветвей схемы
24) 
Метод контурных токов в матричной форме.
Токи в ветвях связи называются контурными токами, и каждый из них рассматривается как непрерывно циркулирующий в своем главном контуре.
İ4= İ11;İ5= İ22; İ6= İ33
При этом ветви дерева являются общими для нескольких контуров, а токи в них определяются как алгебраические суммы соответствующих контурных: İ1= İ11- İ33; İ2= İ22- İ11; İ3= İ33- İ22.
После выражения токов ветвей дерева, подстановки их в уравнения второго закона Кирхгофа и группировки слагаемых с одноименными контурными токами получим систему уравнений в общем виде:
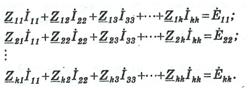Эта система может быть записана в виде матричного уравнения [Zk][ İk]=[Ėk], где [ İk]- столбцовая матрица неизвестных контурных токов. Далее вычисляется матрица сопротивлений [Zk]=[B][Z][B]T, затем находят значение ЭДС, при этом необходимо учитывать и источники тока [Ėk]=[B][Ė]-[B][Z][ İ].
|
|
|
Решением системы являются контурные токи, через которые затем определяются токи в обобщенных ветвях: [İ]=[B]T[İk].
Метод узловых потенциалов в матричной форме.
Формирование системы уравнений связано с выражением всех токов через потенциалы узловых точек и подстановкой их в уравнение первого закона Кирхгофа.
После подстановки получим:
Система может быть записана в виде матричного уравнения[Yy][ϕ]=[ İy], где [ϕ]- столбцовая матрица неизвестных потенциалов, [Yy]- симметричная матрица узловых проводимостей, [ İy]- столбцовая матрица узловых токов.
В общем случае [Yk]=[A][Y][A]T, [İy]=[A][ İ]-[A][Y][ Ė], результатом решения являются потенциалы узловых точек, через которые затем определяются токи в ветвях
Основные понятия, относящиеся к переменным и синусоидальным токам (мгновенное и амплитудное значение, период, частота, фаза, начальная фаза). Диапазон частот, применяемый в технике.
Переменным током (напряжением, ЭДС и т.д.) называется ток, изменяющийся во времени. Ток (напряжение, ЭДС) называется периодическим, если его значения повторяются через одинаковые промежутки времени, а время. Через которое начинаются эти повторения, называются периодом Т, обратная величина – частота. Диапазон частот, применяемых в технике: от сверхнизких частот (0.01-10Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) до сверхвысоких (3000-300000 МГц – миллиметровые волны, радиолокация, радиоастрономия) В РФ промышленная частота 50 Гц. Мгновенным значением тока называется его значение в данный момент времени. Наибольшее мгновенное значение переменной величины за период называется амплитудой.
|
|
|
i=Imsin(ωt+ψ), ωt+ψ- фаза периодических колебаний, ψ- начальная фаза.
27) 
Способы получения переменных токов. Принцип действия машинного генератора переменного тока.
1, 3,.5 -концы обмотки статора;
2 - статор;
4 - ротор;
6 - магнитные силовые линии
Генератор переменного тока состоит из 2 частей: 1) неподвижный статор, 2) вращающийся ротор. На роторе обмотка возбуждения, которая через кольца подключена к источнику постоянной ЭДС, на обмотке возбуждения протекает постоянный ток при вращении ротора, например с помощью турбины, в обмотке статора наводится ЭДС. С обмотки статора снимается напряжения, которое подается в электрическую сеть.
|
|
|
