 |
Линейные пассивные четырёхполюсники. Уравнения типа «А». Обобщённые параметры. Связь между коэффициентами.
|
|
|
|

| Часть электрической цепи или какое-либо электротехническое устройство, имеющие два входных и два выходных зажима (полюса), называют четырехполюсником. Пару зажимов четырехполюсника, к которым присоединяют источник энергии, называют входными, а пару зажимов, к которым присоединяют нагрузку (приемник),- выходными. Четырехполюсники подразделяются на пассивные и активные. Четырехполюсник, в схеме которого не содержатся источники энергии, называется пассивным. Четырехполюсник, в схеме которого есть источники энергии, называется активным. К пассивным четырехполюсникам можно отнести трансформаторы, линии передачи электрической энергии, электрические частотные фильтры, измерительные мосты и ряд других устройств. К активным четырехполюсникам можно отнести, например, усилители, мостовую схему, в одну из диагоналей которой включен источник энергии, а в другую - нагрузка и т. п. Четырехполюсник принято изображать в виде прямоугольника, обозначая входные зажимы 1, 1', а выходные - 2, 2' (рис. 3.1). Если четырехполюсник активный, то в прямоугольнике ставят букву А. Если буквы А нет, то четырехполюсник пассивный. Следует отметить, что если в схеме линейного пассивного четырехполюсника содержатся источники энергии, то обязательно их действие должно взаимно компенсироваться таким образом, чтобы напряжение на входных и на выходных разомкнутых зажимах четырехполюсника было равно нулю. Если линейный четырехполюсник активный, то на одной или на обеих парах его разомкнутых зажимов обязательно должно обнаруживаться напряжение. Четырехполюсники могут быть симметричными и несимметричными. Если при замене входных зажимов выходными (и наоборот) режим работы участков цепей, присоединенных к четырехполюснику, не изменяется, то четырехполюсник симметричный (т. е. симметричный четырехполюсник со стороны выходных зажимов представляет ту же цепь, что и со стороны входных зажимов). В противном случае четырехполюсник будет несимметричный. Четырехполюсники бывают обратимыми и необратимыми. Четырехполюсники, для которых отношение напряжения на входе к току на выходе или отношение напряжения на выходе к току на входе, т. е. взаимные сопротивления входного и выходного контуров, не зависят от того, какие зажимы являются входными, а какие - выходными, называются обратимыми. Отметим, что линейные пассивные четырехполюсники являются обратимыми. В электрических цепях четырехполюсники часто используют в качестве передаточных звеньев между источником питания и нагрузкой. В этом случае предполагается, что изменяться могут нагрузка и напряжение на входе, но сама схема четырехполюсника и сопротивления ее элементов остаются неизменными. Активные четырехполюсники могут быть заменены эквивалентными ему пассивными четырехполюсниками с двумя вынесенными эквивалентными ЭДС. Основной смысл теории четырехполюсника заключается в том, что, используя некоторые обобщенные параметры, можно связать между собой напряжения и токи на входе и выходе четырехполюсника, т. е. находить токи и напряжения на его входе и выходе, не производя расчетов токов и напряжений в схеме самого четырехполюсника. Теория четырехполюсников позволяет при анализе работы цепей сопоставлять и правильно оценивать передающие свойства различных электрических цепей, а также решать задачи синтеза, т. е. определять структуру и элементы четырехполюсников по заданным характеристикам. |
Для определения входных и выходных величин четырехполюсника применяются некоторые обобщенные параметры свойственные всем четырехполюсникам независимо от того что внутри них находится.
Большую разветвлённую электрическую цепь можно рассматривать как соединенные определённым образом простейшие четырехполюсники. При этом анализ достаточно сложной электрической цепи упрощается из-за сокращения числа входящих в нее величин.
Независимо от структуры четырехполюсника, полученные входные и выходные величины позволяют определить его передаточные свойства. Также известные характеристики четырехполюсника помогают определить его структуру.
|
|
|
|
|
|
Системы уравнений четырехполюсника Основной задачей теории четырехполюсников является установление соотношений между четырьмя величинами: напряжениями на входе и выходе, а также токами, протекающими через входные и выходные зажимы. Уравнения, дающие зависимость между U1, U2, I1 и I2, называются уравнениями передачи четырехполюсника. Для линейных четырехполюсников эти уравнения будут линейными. Величины, связывающие в уравнениях передачи напряжения и токи, называются параметрами четырехполюсников.
Сложная электрическая цепь (например, канал связи), имеющая входные и выходные зажимы, может рассматриваться как совокупность четырехполюсников, соединенных по определенной схеме. Зная параметры этих четырехполюсников, можно вычислить параметры сложного четырехполюсника и получить тем самым зависимость между напряжениями и токами на зажимах результирующего сложного четырехполюсника, не производя расчетов всех напряжений и токов внутри заданной схемы. Кроме того, теория четырехполюсников позволяет решить обратную задачу: по заданным напряжениям и токам найти параметры четырехполюсника и затем построить его схему и рассчитать элементы, т. е. решить задачу синтеза. Пусть четырехполюсник содержит п независимых контуров. Отнесем первый контур ко входу четырехполюсника (Iк1 = I1), второй контур - к его выходу (Iк2 = I2). Будем считать, что во внутренних контурах четырехполюсника отсутствуют независимые источники энергии. При рассмотрении четырехполюсника важно заранее условиться о положительных направлениях напряжений и токов. В дальнейшем будем придерживаться положительных направлений, показанных стрелками на рис. 12.1, если особо не будут оговорены другие случаи. Составим систему уравнений для контурных токов (см. § 2.4):
|
|
|
 |
Определим из этой системы токи I1 и I2.
 |
где DZ - определитель системы уравнений (12.1); D11, D22, D12 и D21 - алгебраические дополнения определителя DZ. Введем обозначения
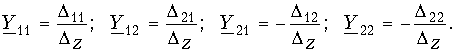 |
 |
Тогда
Коэффициенты Y11, Y12, Y21 и Y22 в уравнениях (12.2) называются Y-параметрами, или параметрами проводимостей четырехполюсника, так как по размерности они являются именно таковыми. Уравнения (12.2) называются уравнениями передачи четырехполюсника в Y-параметрах. Эти уравнения представляют собой одну из возможных форм уравнений передачи. Она позволяют находить любую пару из значений I1, I2, U1 и U2, если заданы значения другой пары.
Помимо уравнений в форме (12.2) существует еще пять форм уравнений передачи. Уравнения, связывающие напряжения U1, U2 и токи I1, I2

 |
содержат в качестве коэффициентов параметры сопротивлений четырехполюсника, или Z-параметры, и называются уравнениями передачи в Z-параметрах. Параметры Z11, Z12, Z21 и Z22 имеют размерность сопротивлений. Заметим, что они не являются обратными величинами по отношению к параметрам проводимости, таким образом, например
Не следует также путать эти параметры с собственными и взаимными сопротивлениями контуров Z11, Z12 и т. д. в уравнениях (12.1) для контурных токов. Коэффициенты, входящие в систему уравнений, связывающую входные U1 и I1 и выходные U2 и I2 напряжения и токи
 |
называются апараметрами, или обобщенными параметрами. Уравнения (12.4) называются уравнениями передачи в апараметрах. Параметры A11 и A22 являются безразмерными, параметр A12 имеет размерность сопротивления; параметр A21 - размерность проводимости.
Приведем еще две формы уравнений передачи:

|
|
|


