Главная | Обратная связь | Поможем написать вашу работу!

Практическое занятие №5«Выполнение тождественных преобразований в тригонометрических выражениях» 1 глава

Практическое занятие №1

«Элементы комбинаторики, теории вероятностей и математической статистики»

Практическое занятиерассчитано на 2 часа, относится к теме «Элементы математической статистики

Формируемые компетенции: У20, У21, У22, З1, З2, З3, З4

Цель: научиться решать задачи с использованием формул комбинаторики, теории вероятности и математической статистики.

Методическое и техническое обеспечение:

- методические указания к выполнению практического занятия;

- комплекты учебно-наглядных пособий по соответствующим разделам математики.

- мультимедийный проектор;

- ноутбук;

- проекционный экран;

- компьютерная техника для обучающихся с наличием лицензионного программного обеспечения;

- комплект слайд-презентаций.

Теоретические сведения

Комбинаторика – раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам.

Многие комбинаторные задачи могут быть решены с помощью двух правил – правила умножения и правила сложения.

Правило умножения: если из некоторого конечного множества первый объект (элемент а) можно выбрать n₁ способами, а второй объект (элемент b) – n₂ способами, то оба объекта (a и b) в указанном порядке можно выбрать способами.

Правило сложения: если некоторый объект а можно выбрать n₁ способами, а объект b можно выбрать n₂ способами, причем первые и вторые способы не пересекаются, то любой из объектов (a или b) можно выбрать способами.

Существует две схемы выбора k элементов из заданного множества: без возвращения, когда выбранные элементы не возвращаются в исходное множество, и с возвращением, когда выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге.^*

О1: Размещениями из n элементов по k элементов называются всевозможные комбинации из k элементов, отличающиеся друг от друга либо составом, либо порядком элементов. Обозначают .

О2: Сочетаниями из n элементов по k элементов называются всевозможные комбинации из k элементов, отличающиеся друг от друга хотя бы одним элементов. Обозначают .

О3: Перестановками из n элементов называются всевозможные комбинации n элементов, отличающиеся друг от друга только их порядком.

Обозначают .

Формулы для вычисления числа возможных комбинаций во всех перечисленных случаях приведены в следующей таблице:

Соединения	Схема выбора без возвращения.	Схема выбора с возвращением.
Размещения
Сочетания
Перестановки		где число элементов i вида

Замечание:

Классическое определение вероятности.

Пусть производится опыт с равновозможными исходами, образующими полную группу несовместных событий. Такие исходы называют элементарными исходами (событиями). Случай, который приводит к наступлению события , называется благоприятным ему.

О: Вероятность события называется отношение числа случаев, благоприятствующих этому событию, к общему числу случаев.

(1)

Вероятность события численно характеризует степень возможности его появления в рассматриваемом опыте.

Теорема сложения вероятностей двух событий.

Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления:

(2)

Теорема сложения вероятностей двух несовместных событий.

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий

(3)

Следствие. Сумма вероятностей противоположных событий равна единице:

Теорема умножения вероятностей двух независимых событий.

Вероятность произведения двух независимых событий равна произведению их вероятностей.

(4)

Статистические характеристики

Среднее арифметическое, размах и мода

Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.

Среднее арифметическое находят тогда, когда хотят определить среднее значение для некоторого ряда данных: среднюю урожайность пшеницы с 1 га в районе, средний суточный удой молока от одной коровы на ферме, среднюю выработку одного рабочего бригады за смену и т. п.

Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.

Пусть, например, в течение суток отмечают каждый час температуру воздуха в городе. Для полученного ряда данных полезно не только вычислить среднее арифметическое, показывающее, какова среднесуточная температура, но и найти размах ряда, характеризующий колебание температуры воздуха в течение этих суток.

Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.

Ряд чисел может иметь более одной моды или не иметь моды совсем.

Например, в ряду чисел 47, 46, 50, 52, 47, 52, 49, 45, 43, 53 две моды — это числа 47 и 52, так как каждое из этих чисел встречается два раза, а остальные числа встречаются в ряду менее двух раз, а в ряду чисел

69, 68, 66, 70, 67, 71, 74, 63, 73, 72 моды нет.

Заметим, что среднее арифметическое ряда чисел может не совпадать ни с одним из этих чисел, а мода, если она существует, обязательно совпадает с двумя или более числами ряда.

Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Пример выполнения задания

Пример 1. Сколько различных перестановок букв можно сделать в словах:

а) замок;

б) топор;

в) колокол.

Решение.

а) В слове замок все буквы различны, всего их пять. По формуле получаем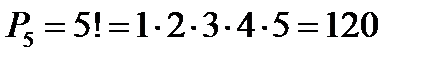

б) В слове топор буква о повторяется дважды, поэтому

в) В слове колокол, состоящем из семи букв буква к- встречается дважды 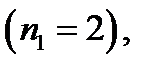буква о – трижды буква л – дважды поэтому

Пример 2. Сколькими различными способами можно выбрать три лица из десяти кандидатов на три:

а) различные должности;

б) одинаковые должности;

Решение.

а) Так как назначение проходит на три различные должности, то важно не только, кто попадет в выбранную тройку, но и порядок выбора внутри самой тройки. Таким образом, мы имеем дело с размещением.

б) Учитывая, что должности одинаковые, делаем вывод: порядок кандидатов внутри выбранной тройки не важен. Следовательно, по формуле получаем: .

Пример 3. Пять человек вошли в лифт на 1-м этаже девятиэтажного дома. Сколькими способами пассажиры могут выйти из лифта на нужных этажах.

Решение. Каждый из пяти пассажиров может выйти на любом из восьми этажей со 2-го по 9-ый включительно. Учитывая, что на каждом из этажей может выйти не один пассажир, получаем схему «с возвращением», а именно

Этот же результат можно получить, используя правило умножения: для 1-го пассажира имеется 8 вариантов выхода на этаже, для 2-го тоже 8, и для 3-го – 8, и для 4-го – 8, и для 5-го – 8. Всего получается вариантов выхода 5-ти пассажиров.

Пример 4. В магазине имеется 7 видов тортов. Сколькими способами можно составить набор, содержащий 3 торта? А если имеются 3 вида тортов, а нужен набор из 7 тортов?

Решение.

Поскольку порядок расположения тортов в наборе не играет роли, то искомое число наборов равно числу сочетаний с повторениями из 7 элементов по 3 в каждом.

Если имеется три вида тортов, а нужен набор из 7 тортов, то число возможных наборов равно

Пример 5. Сколькими способами могут быть расставлены 8 участниц финального забега на восьми беговых дорожках?

Число способов равно числу перестановок из 8 элементов. По формуле числа перестановок находим, что

Значит, существует 40 320 способов расстановки участниц забега на восьми беговых дорожках.

Пример 6. Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 2, 4, 6?

Из цифр 0, 2, 4, 6 можно получить перестановок. Из этого числа надо исключить те перестановки, которые начинаются с 0, так как натуральное число не может начинаться с цифры 0. Число таких перестановок равно . Значит, искомое число четырехзначных чисел (без повторения цифр), которые можно составить из цифр 0, 2, 4, 6, равно Получаем:

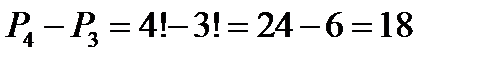Пример 7. Имеется девять различных книг, четыре из которых — учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом?

Сначала будем рассматривать учебники, как одну книгу. Тогда на полке надо расставить не девять, а шесть книг. Это можно сделать способами. В каждой из полученных комбинаций можно выполнить перестановок учебников. Значит, искомое число способов расположения книг на полке равно произведению . Получаем: .

Пример 8. Сколько трехзначных чисел (без повторения цифр в записи числа) можно составить из цифр 0, 1, 2, 3, 4, 5, 6?

Если среди семи цифр нет нуля, то число трехзначных чисел (без повторения цифр), которые можно составить из этих цифр, равно числу размещений из 7 элементов по 3. Однако среди данных цифр есть цифра 0, с которой не может начинаться трехзначное число. Поэтому из размещений из 7 элементов по 3 надо исключить те размещения, у которых первым элементом является цифра 0. Их число равно числу размещений из 6 элементов по 2.

Значит, искомое число трехзначных чисел равно .

Получаем: .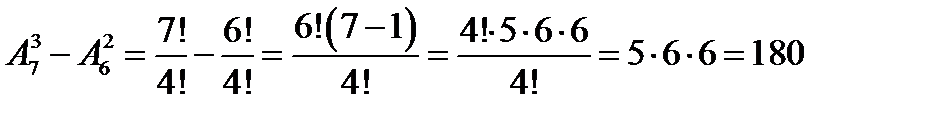

Из данных цифр можно составить 180 трехзначных чисел.

Пример 9. Дано шесть карточек с буквами Н, М, И, Я, Л, О.Найти вероятность того, что:

а) получится слово ЛОМ, если наугад одна за другой выбираются три карточки;

б) получится слово МОЛНИЯ, если наугад одна за другой выбираются шесть карточек и располагаются в ряд в порядке появления.

Решение.

а) Из шести данных букв можно составить трехбуквенных “слов” (НИЛ, ОЛЯ, ЛЯМ,…). Слово ЛОМ появится при этом лишь один раз, т. е .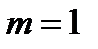

Пусть событие -{появилось слово ЛОМ}.

Тогда по формуле (1):

б) Шестибуквенные “слова” отличаются друг от друга лишь порядком расположения букв (НОЛМИЯ, ЯНОЛИМ,…). Их число равно числу перестановок из 6 букв, т.е. . Очевидно, что . Тогда вероятность появления слова МОЛНИЯ (событие В) равна (по формуле 1):

Пример 10. Два стрелка делают по одному выстрелу в мишень. Вероятность попадания первого стрелка 0,7, а второго – 0,8. Найти вероятность того, что мишень будет поражена?

Решение.

Поражение цели (С) означает, что: в неё попал первый стрелок, а второй «промазал» ; или попал второй стрелок, а первый «промазал» ; или попали оба стрелка .

Т.к. события , и несовместные, то по формуле (3), получим

Пример 11. При изучении учебной нагрузки учащихся выделили группу из 12 семиклассников. Их попросили отметить в определенный день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные: 23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.

Имея этот ряд данных, можно определить, сколько минут в среднем затратили учащиеся на выполнение домашнего задания по алгебре.

Для этого указанные числа надо сложить и сумму разделить на 12:

Число 27, полученное в результате, называют средним арифметическим рассматриваемого ряда чисел.

В рассмотренном примере мы нашли, что в среднем учащиеся затратили на выполнение домашнего задания по алгебре по 27 мин. Однако анализ приведенного ряда данных показывает, что время, затраченное некоторыми учащимися, существенно отличается от 27 мин, т. е. от среднего арифметического. Наибольший расход равен 37 мин, а наименьший— 18 мин. Разность между наибольшим и наименьшим расходом времени составляет 19 мин. В этом случае говорят, что размах ряда равен 19. Модой данного ряда является число 25.

Пример 12. Пусть, проведя учет деталей, изготовленных за смену рабочими одной бригады, получили такой ряд данных:

36, 35, 35, 36, 37, 37, 36, 37, 38, 36, 36, 36, 39, 39, 37, 39,

Найдем для него среднее арифметическое, размах и моду. Для этого удобно предварительно составить из полученных данных упорядоченный ряд чисел, т. е. такой ряд, в котором каждое последующее число не меньше (или не больше) предыдущего. Получим

35, 35, 36, 36, 36, 36, 36, 36, 36, 36, 37, 37, 37, 37, 38, 38, 38, 39, 39, 39, 39.

Вычислим среднее арифметическое:

Размах ряда равен 39-35=4. Мода данного ряда равна 36, так как число 36 чаще всего встречается в этом ряду.

Итак, средняя выработка рабочих за смену составляет примерно 37 деталей; различие в выработке рабочих не превосходит 4 деталей; типичной является выработка, равная 36 деталям.

Пример 13. При сборе данных о расходе электроэнергии получили такую таблицу:

Номер квартиры	1	2	3	4	5	6	7	8	9	10
Расход электроэнергии, кВт-ч	85	64	78	93	72	91	72	75	82	88

Представим полученные данные в виде упорядоченного ряда чисел:

64, 72, 72, 75, 78, 82, 85, 88, 91, 93.

В этом числовом ряду четное число членов и имеются два числа, расположенные в середине ряда: 78 и 82. Найдем среднее арифметическое этих чисел: 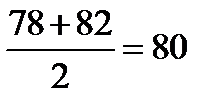. Число 80, не являясь членом ряда, разбивает этот ряд на две одинаковые по численности группы: слева от него находится пять членов ряда и справа тоже пять членов ряда:

64, 72, 72, 75, 78, , 82, 85, 88, 91, 93.

Говорят, что в этом случае медианой рассматриваемого упорядоченного ряда, а также исходного ряда данных, записанного в таблице, является число 80.

Порядок выполнения практического задания:

1. Выполнить задания.

2. Ответить на вопросы для закрепления теоретического материала.

3. Оформить отчёт.

Содержание отчета: выполнить задания письменно на листах формата А4.

Контрольные вопросы:

1. Какие соединения называют размещениями?

2. Выпишите формулу для числа размещений из n элементов по m.

3. Какие соединения называются перестановками?

4. Выпишите формулу для числа перестановок из n элементов.

5. Какие соединения называются сочетаниями?

6. Выпишите формулу для числа сочетаний из n элементов по m.

7. Какие случайные события называются достоверными и какие невозможными?

8. Какие события называются несовместными?

9. Какие события называются совместными?

10. Какие события называются противоположными?

11. Дайте классическое определение вероятности.

12. Сформулируйте теорему сложения вероятностей несовместных событий.

13. Сформулируйте теорему сложения вероятностей совместных событий.

14. Чему равна сумма вероятностей двух противоположных событий?

15. Что называется условной вероятностью события?

16. Какие события в совокупности называются независимыми?

17. Сформулируйте теорему умножения вероятностей независимых событий.

18. Сформулируйте теорему умножения вероятностей зависимых событий.

Список литературы

1 Башмаков М.И. Математика. Сборник задач профильной направленности М.: Академия Гриф 2013

2. Башмаков Н.А Математика М.: Академия Гриф 2011

3. www. fcior. edu. ru Информационные, тренировочные и контрольные материалы

4. www. school-collection. edu. Ru Единая коллекции цифровых образовательных ресурсов

Индивидуальные задания

Вариант № 1

1. Решить уравнение .

2. На собрании должны выступить 4 человека (A, B, C, D). Сколькими способами их можно разместить в списке выступающих, если B должен выступать последним?

3. Сколькими способами можно распределить 6 разных книг между 3 школьниками?

4. Для новогодней лотереи отпечатали 1500 билетов, из которых 120 выигрышных. Какова вероятность того, что купленный билет окажется выигрышным?

5. Найдите среднее арифметическое, размах и моду ряда чисел: 16; 22; 16; 13; 20; 17.

6. Вероятность того, что студент сдаст первый экзамен 0,9, второй – 0,9, третий – 0,8. Найти вероятность того, что студентом будет сдан только первый экзамен.

Вариант № 2

1. Решить уравнение .

2. Сколькими способами могут разместиться 7 человек вокруг круглого стола?

3. Четыре человека случайно отбираются из 10 согласившихся участвовать в интервью для выяснения их отношения к продукции фирмы по производству продуктов питания. Эти 4 человека прикрепляются к 4 интервьюерам. Сколько существует различных способов составления таких групп, если выбор случаен?

4. Какова вероятность того, что при бросании игрального кубика выпадет 1 очко?

5. Имеются следующие данные о распределении участников похода по возрасту:

Возраст, лет	18-22	22-26	26-30	30-34
Число участников	25	18	5	2

Заменив каждый интервал его серединой, найдите средний возраст участников похода.

6. Брошены монета и игральный кубик. Найти вероятность совмещения событий «появления герба» и «появление нечётного числа».

Вариант № 3

1. Решить уравнение

2. Фирма нуждается в организации 4 новых складов. Её сотрудники подобрали 8 подходящих одинаково удобных помещений. Сколько существует способов отбора 4 помещений из 8 в случайном порядке?

3. Дано множество чисел 1, 2, 3, 4, 5. Сколько можно составить пятизначных чисел, которые не начинаются на 3 или 5?

4. В «Словаре русского языка» С.И. Ожегова 900 страниц. Какова вероятность того, что наугад открытая страница будет иметь порядковый номер 113?

5. В фермерском хозяйстве отведены под пшеницу три участка, площади которых равны 12 га, 8 га и 6 га. Средняя урожайность на первом участке составляет 18 ц с 1 га, на втором— 19 ц с 1 га, на третьем — 23 ц с 1 га. Чему равна средняя урожайность пшеницы в этом хозяйстве?

6. Рабочий обслуживает 3 станка. Вероятность того, что в течении смены потребует его внимания первый станок, равна 0,7; второй – 0,6; третий – 0,55. Найти вероятность того, что в течение смены потребуют внимания рабочего какие-нибудь два станка.

Вариант № 4

1. Решить уравнение

2. Для разгрузки поступивших товаров менеджеру требуется выделить 6 из 20 имеющихся рабочих. Сколькими способами можно это сделать, осуществляя отбор в случайном порядке?

3. В шахматном турнире принимают участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий сыграно в этом турнире?

4. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар?

5. На соревнованиях по фигурному катанию судьи поставили спортсмену следующие оценки: 5,2, 5,4, 5,5, 5,4, 5,1, 5,1, 5,4, 5,5, 5,3. Для полученного ряда чисел найдите среднее арифметическое, размах и моду.

6. В первой урне 1 белый и 4 черных шара, во второй – 2 белых и 3 черных, в третьей – 3 белых и 4 черных шара. Из каждой урны взяли по шару. Какова вероятность того, что среди вынутых шаров будет 1 белый и 2 черных шара?

Вариант № 5

1. Решить уравнение

2. Руководство фирмы может обратиться в 6 туристических агентств с просьбой об организации для своих сотрудников трех различных туристических поездок. Сколько существует способов распределения трех заявок между шестью агентствами, если каждое агентство может получить не более одной заявки?

3. Бригадир должен отправить на работу бригаду из 3человек. Сколько таких бригад можно составить из 8 человек?

4. В урне 12 шаров: 3 белых, 4 черных и 5 красных. Какова вероятность вынуть из урны чёрный шар?

5. В ряду чисел: 2, 7, 10, _, 18, 19, 27 одно число оказалось стертым. Восстановите его, зная, что среднее арифметическое этих чисел равно 14.

6. Охотник выстрелил 3 раза по удалявшейся мишени. Вероятность попадания в неё при первом выстреле равна 0,8, а после каждого выстрела она уменьшается на 0,1. Найти вероятность того, что охотник: а) промахнётся все 3 раза; б) попадёт 2 раза.

Вариант № 6

1. Решить уравнение

2. Сколько трехзначных чисел можно составить из цифр 0, 4, 5, если каждая цифра входит в изображение числа только один раз?

3. В классе изучается 7 предметов. Сколькими способами можно составить расписание на понедельник, если в этот день должно быть 5 различных предметов?

4. В урне 12 шаров: 3 белых, 4 черных и 5 красных. Какова вероятность вынуть из урны белый шар?

5. Среднее арифметическое ряда, состоящего из девяти чисел, равно 13. Из этого ряда вычеркнули число 3. Чему равно среднее арифметическое нового ряда чисел?

6. Имеется три ящика, содержащих по 10 деталей. В первом ящике 8, во втором 2 и в третьем 7 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вытянутые детали окажутся нестандартными.

12 3 4 5 Следующая ⇒

Воспользуйтесь поиском по сайту: