Практическое занятие №5«Выполнение тождественных преобразований в тригонометрических выражениях» 2 глава

Вариант № 7

1. Решить уравнение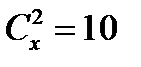

2. Выделены крупные суммы на выполнение четырех правительственных программ, сулящих исполнителям высокую прибыль. Сколько существует способов случайного распределения этих четырех программ между шестью возможными исполнителями?

3. На собрании должны выступить 5 человек (A, B, C, D, E). Сколькими способами их можно разместить в списке выступающих, если B должен выступать первым?

4. В урне 12 шаров: 3 белых, 4 черных и 5 красных. Какова вероятность вынуть из урны красный шар?

5. В таблице показан расход электроэнергии некоторой семьей в течение года:

 

Месяц	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII
Расход электроэнергии, кВт*ч	85	80	74	61	54	34	32	32	62	78	81	83

6. Вероятность того, что студент сдаст первый экзамен 0,9, второй – 0,9, третий – 0,8. Найти вероятность того, что студентом будут сданы только первый и третий экзамены.

Вариант № 8

1. Решить уравнение

2. Из группы в 15 человек выбирают 4-х участников эстафеты . Сколькими способами можно расставить спортсменов на этих этапах?

3. На 9 вакантных мест по определенной специальности претендуют 15 безработных, состоящих на учете в службе занятости. Сколько возможно комбинаций выбора 9 из 15 безработных?

4. Какова вероятность того, что произвольно взятое трехзначное число делится на 3?

5. Среднее арифметическое ряда, состоящего из десяти чисел, равно 15. К этому ряду приписали число 37. Чему равно среднее арифметическое нового ряда чисел?

6. Два стрелка делают по одному выстрелу в цель. Вероятность попадания для первого стрелка равна 0,7, для второго – 0,8. Найти вероятность того, что попадут в цель: а)оба стрелка; б) только один; в) ни один.

Вариант № 9

1. Число сочетаний из n элементов по 3 в 5 раз меньше числа сочетаний из n +2 по 4. Найти n.

2. По сведениям геологоразведки один из 15 участков земли по всей вероятности содержит нефть. Однако компания имеет средства для бурения только 8 скважин. Сколько способов отбора восьми различных скважин у компании?

3. Сколькими способами можно распределить 12 классных комнат под 12 учебных кабинетов.

4. В таблице приведены данные о продаже в течение недели картофеля, завезенного в овощную палатку:

День недели	Пн	Вт	Ср	Чт	Пт	Сб	Вс
Количество картофеля, кг	275	286	250	290	296	315	325

 

Сколько картофеля в среднем продавали ежедневно в эту не­делю?

5. Брошены 2 игральные кости. Найти вероятность того, что:

а) сумма выпавших очков не превосходит 7;

б) на обеих костях выпадет одинаковое число очков;

6. Брошены монета и игральный кубик. Найти вероятность совмещения событий «появление герба» и «появление чётного числа».

Вариант № 10

1. Решить систему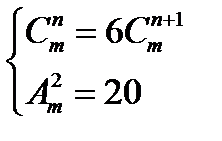

2. Пять фирм F1, F2, F3, F4, F5 предлагают свои условия по выполнению трех различных контрактов C1, C2 и C3.Любая фирма может получить только один контракт. Контракты различны, то есть, если контракт C1 получит фирма F1, то это не то же самое, если фирма F 1 получит контракт C2. Сколько способов получения контрактов имеют фирмы?

3. Сколько двухзначных, трехзначных чисел можно составить из цифр 7,2,5, если каждая цифра входит в изображение числа только один раз?

4. Монету подбросили три раза. Какова вероятность того, что «решка» выпала один раз?

5. Найдите среднее арифметическое, размах и моду ряда чисел: 18; 22; 18; 13; 24; 15.

6. Вероятность того, что книга имеется в фондах первой библиотеки, равна 0,5, второй 0,7 и в третьей – 0,4. Определить вероятность того, что книга имеется в фондах: а)двух библиотек;

 

Вариант № 11

1. Решите уравнение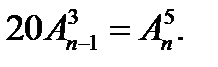

2. Для доступа в компьютерную сеть оператору необходимо набрать пароль из 4 цифр. Оператор забыл или не знает необходимого кода. Сколько всевозможных комбинаций он может составить для набора пароля, если цифры в коде не повторяются? 

3. Если подбросить одновременно три игральные кости, то сколько имеется различных комбинаций выброшенных очков?

4. Какова вероятность того, что выбранное наудачу двузначное число содержит 5?

5. Имеются следующие данные о распределении участников похода по возрасту:

 

Возраст, лет	18-22	22-26	26-30	30-34
Число участников	24	13	4	4

 

Заменив каждый интервал его серединой, найдите средний возраст участников похода.

6. Из трех орудий произвели залп по цели. Вероятность попадания из первого орудия равна равна 0,8; из второго – 0,6; из третьего – 0,9. Найти вероятность того, что: а) только один снаряд попадет в цель; б) два снаряда попадут в цель?

 

Вариант № 12

1. Число сочетаний из элементов по 3 в 5 раз меньше числа сочетаний из 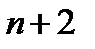 по 4. Найдите n.

2. Сколькими способами 3 награды (за I, II, III, места) могут быть распределены между 10 участниками соревнований?

3. 4 пианиста, 5 скрипачей и 8 баянистов участвуют в конкурсе. Сколькими способами жюри может отобрать по три победителя в каждой номинации?

4. Подбрасывают два игральных кубика. Какова вероятность, что сумма выпавших очков равна 9.

5. При изучении качества продукции, выпущенной цехом, определяли число бракованных деталей в каждом из 50 произвольным образом выбранных ящиков с одинаковым числом деталей. Получили такую таблицу:

Число бракованных деталей	0	1	2	3	4
Число ящиков	6	20	13	6	5

 

 

Найдите среднее арифметическое, размах и моду полученного ряда данных.

6. Симметричная монета подброшена три раза. Какова вероятность того, что «орел» выпадет ровно два раза?

Вариант № 13

1. Решить уравнение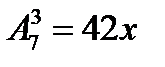

2. Сколько существует способов составления списка 8 деловых звонков случайным образом?

3. Необходимо отправить на матч команду из 7 человек. Сколько таких команд можно составить из 18 человек?

4. Монету подбросили три раза. Какова вероятность того, что «решка» выпала два раза?

5. Найдите среднее арифметическое, размах и моду ряда чисел: 18; 26; 18; 13; 26; 17.

6. Вероятность попадания при одном выстреле первым стрелком 0,3, вторым – 0,4, третьим – 0,8. Найти вероятность того, что попадут только два стрелка.

Вариант № 14

1. Решите уравнение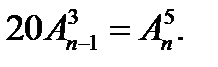

2. Дано множество чисел 7, 2, 8, 4, 6. Сколько можно составить пятизначных чисел, которые не начинаются на 7 или 4?

3. Владимир хочет пригласить в гости троих из семи своих лучших друзей. Сколькими способами он может выбрать приглашенных?

4. Подбрасывают два игральных кубика. Какова вероятность, что сумма выпавших очков равна 8?

5. При изучении качества продукции, выпущенной цехом, определяли число бракованных деталей в каждом из 50 произвольным образом выбранных ящиков с одинаковым числом деталей. Получили такую таблицу:

Число бракованных деталей	0	1	2	3	4
Число ящиков	8	17	13	5	7

 

Найдите среднее арифметическое, размах и моду полученного ряда данных.

6. Вероятность попадания в мишень для первого спортсмена 0,85, а для второго – 0,8. Спортсмены независимо друг от друга сделали по одному выстрелу. Найти вероятность того, что в мишень попадёт хотя бы один спортсмен?

Вариант № 15

1. Решить уравнение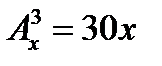

2. Сколько четырехзначных чисел можно составить из цифр 8, 4, 5, 0, если каждая цифра входит в изображение числа только один раз?

3. Из группы в 15 человек выбирают 4-х участников эстафеты . Сколькими способами можно расставить спортсменов на этих этапах?

4. В таксопарке 42 машины. Из которых 15 – красных; 10-желтых; остальные – синие. Какова вероятность, что по вызову приедет синее такси?

5. При изучении качества продукции, выпущенной цехом, определяли число бракованных деталей в каждом из 55 произвольным образом выбранных ящиков с одинаковым числом деталей. Получили такую таблицу:

Число бракованных деталей	0	1	2	3	4
Число ящиков	8	20	13	6	8

 

Найдите среднее арифметическое, размах и моду полученного ряда данных.

 

6. В каждом из трёх ящиков имеется по 24 детали; при этом в первом ящике 18, во втором 20, в третьем 22 стандартные детали. Из каждого ящика берут по одной детали. Найти вероятность того, что все три вынутые детали окажутся нестандартными.

Вариант № 16

1. Решить уравнение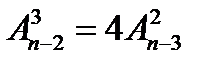

2. Сколькими способами можно выбрать 4 детали из ящика, содержащего 16 деталей?

3. На собрании должны выступить 4 человека (A, B, C, D). Сколькими способами их можно разместить в списке выступающих, если B должен выступать первым?

4. В корзине находится 5 красных и 3 зеленых шара. Какова вероятность того, что наудачу выбранный шар окажется красным?

5. Имеются следующие данные о распределении допусков деталей, мкм:

Допуск, мкм	0-2	2-4	4-6	6-8
Число деталей	25	20	5	0

 

 

Заменив каждый интервал его серединой, найдите средний размер допусков.

6. Брошены монета и игральный кубик. Найти вероятность совмещения событий «появление герба» и «появление чётного числа».

Практическое занятие №2

«Действия над числами. Вычисление погрешностей. Комплексные числа»

Практическое занятие рассчитано на 2 часа, относится к теме «Развитие понятия о числе».

Формируемые компетенции: У1, У2, У4, З1, З2, З3

Цель: Ознакомиться с понятием комплексного числа. Изучить различные формы представления комплексных чисел: алгебраическую, тригонометрическую, показательную. Научиться изображать геометрически комплексное число; выполнять действия над комплексными числами: сложение, вычитание, умножение, деление, возведение в степень (формула Муавра), извлечение корня.

Методическое и техническое обеспечение:

- методические указания к выполнению практического занятия;

- комплекты учебно-наглядных пособий по соответствующим разделам математики.

- мультимедийный проектор;

- ноутбук;

- проекционный экран;

- компьютерная техника для обучающихся с наличием лицензионного программного обеспечения;

- комплект слайд-презентаций.

 

 

Теоретические сведения

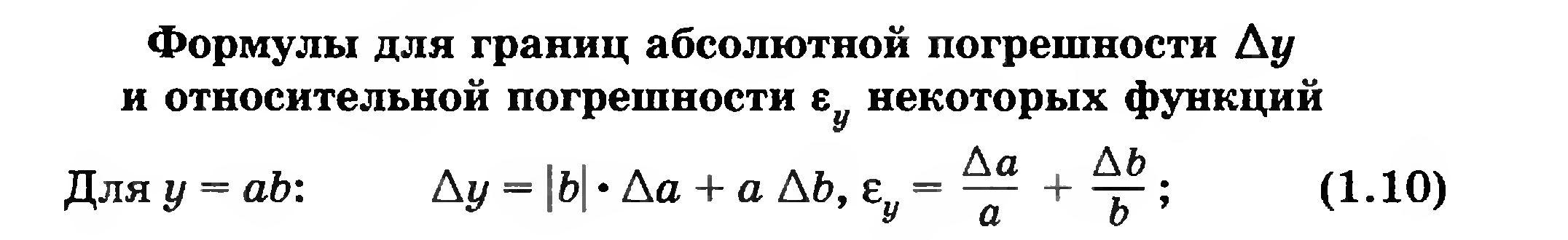
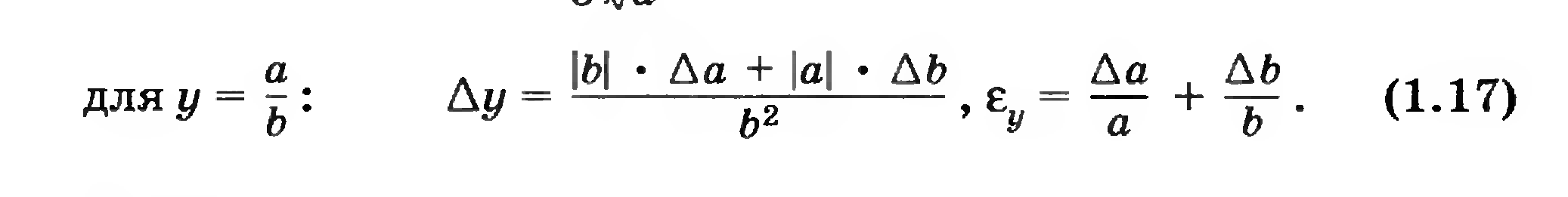
Определение. Комплексным числом z называется упорядоченная пара чисел (а,b), над множеством которых по определенным правилам можно производить следующие операции: сложение, умножение, деление, возведение в степень результаты которых также являются комплексными числами.

Определение. Алгебраической формой комплексного числа z называется выражение , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением: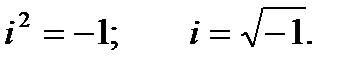

При этом число a называется действительной частью числа z (a = Rez), а b- мнимой частью (b = Imz).

Если a =Rez =0, то число z будет чисто мнимым, если b = Imz = 0, то число z будет действительным.

Определение. Числа  и называются комплексно – сопряженными.

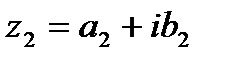Определение. Два комплексных числа  и  называются равными, если соответственно равны их действительные и мнимые части:

Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.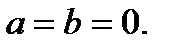

        

                                   у

 

                                                             A(a, b)

 

 

                                            r              b

                                                   j

 

                                 0      a                     x

 

    Таким образом, на оси ОХ располагаются действительные числа a, а на оси ОY – чисто мнимые-b.

        

Действия с комплексными числами.

 

Основные действия с комплексными числами вытекают из действий с многочленами.

 

1) Сложение и вычитание.

 

 

 

2) Умножение.

 

 

 

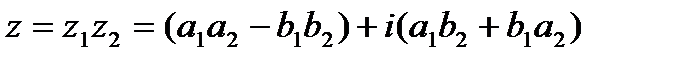
В случае комплексно – сопряженных чисел:

 

3) Деление.

 

 

Пример выполнения задания

Пример 1

Пример 2

Пример 3.Найти сумму комплексных чисел z₁ = 2 – i и z₂ = –4 + 3i.

z₁ + z₂ = (2 + (–1)∙i)+ (–4 + 3i) = (2 + (–4)) + ((–1) + 3) i = –2+2i.

Пример4. Найти произведение комплексных чисел z₁ = 2 – 3i и z₂ = –4 + 5i.

 ₌ (2 – 3i) ∙ (–4 + 5i) = 2 ∙(–4) + (-4) ∙(–3i) + 2∙5i – 3i∙5i =7+22i.

Пример5. Найти частное z от деления z₁ = 3 – 2 на z₂ = 3 – i.

z = .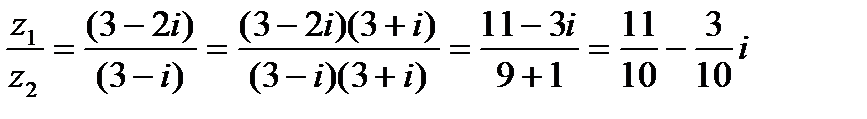

 

Пример №5. Найти модуль комплексных чисел z₁ = 4 – 3i и z₂ = –2–2i.

_;

.

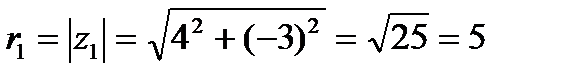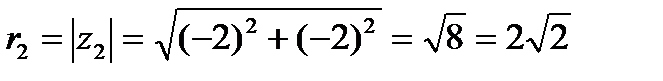Порядок выполнения практического задания:

1. Выполнить задания.

2. Ответить на вопросы для закрепления теоретического материала.

3. Оформить отчёт.

Содержание отчета: выполнить задания письменно на листах формата А4.

Контрольные вопросы:

1. Как вычисляется граница абсолютной погрешности суммы приближенных значений чисел?

2. Как вычисляется граница относительной погрешности суммы приближенных значений чисел?

3. Как вычисляется граница абсолютной погрешности разности приближенных значений чисел?

4. Как вычисляется граница относительной погрешности разности приближенных значений чисел?

5. Как вычисляется граница абсолютной погрешности произведения и частного приближенных значений чисел?

6. Дайте определение комплексного числа (алгебраическая форма записи). Что такое мнимая единица, действительная и мнимая часть комплексного числа?

7. Что называется комплексной плоскостью? Почему комплексное число называют вектором или точкой на комплексной плоскости?

8. Что такое модуль и аргумент комплексного числа, как их найти?

9. Операции над комплексными числами. Дайте определение комплексно-сопряженному числу.

Список литературы

1 Башмаков М.И.    Математика. Сборник задач профильной направленности М.: Академия Гриф 2013

2. Башмаков Н.А    Математика   М.: Академия Гриф 2011

3. www. fcior. edu. ru Информационные, тренировочные и контрольные материалы

4. www. school-collection. edu. Ru Единая коллекции цифровых образовательных ресурсов

Индивидуальные задания

 

Вариант №1

1. Найти абсолютную и относительную погрешности, если известно, что - 0,143 является приближенным значением для .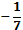

2. Найдите сумму и разность чисел x = 35,49±0,002; у = 1,27±0,003.

3. Найдитезначение выражения:

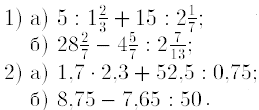
4. Найти z₁ ± z_2, z₁z_2, z₁/z₂, если z1= 5+I; z2=-i

Вариант №2

1. Найти абсолютную и относительную погрешности если известно, что 0,818 является приближенным значением для .

2. Найдите произведение чисел x = 35,49±0,002; у = 1,27±0,003.

3. Найдитезначение выражения:

4. Найти z₁ ± z_2, z₁z_2, z₁/z₂, если z1= 1-i; z2=-8i

Вариант №3

1. Найти абсолютную и относительную погрешности если известно, что 0,154 является приближенным значением для .

2. Найдите частное чисел x = 35,49±0,002; у = 1,27±0,003.

3. Найдите значение выражения:

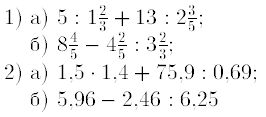
4. Найти z₁ ± z_2, z₁z_2, z₁/z₂, если z1=2+2i; z2=2+i

Вариант №4

1. Найти абсолютную и относительную погрешности если известно, что - 0,286 является приближенным значением для .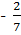

2. Найдите произведение чисел x = 27,15±0,002; у = 16,22±0,003.

3. Найдитезначение выражения:

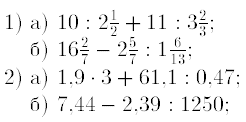
4. Найти z₁ ± z_2, z₁z_2, z₁/z₂, если z1= 1-2i; z2= 3+3i

Вариант №5

1. Найти абсолютную и относительную погрешности если известно, что 0,727 является приближенным значением для .

2. Найдите частное чисел x = 27,15±0,002; у = 16,22±0,003.

3. Найдитезначение выражения:

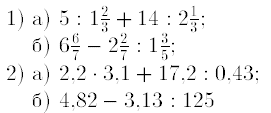
4. Найти z₁ ± z_2, z₁z_2, z₁/z₂, если   z1=-2-2i;    z2= 2+2i

 

Вариант №6

1. Найти абсолютную и относительную погрешности если известно, что 0,308 является приближенным значением для .

2. Найдите сумму и разность чисел x = 12,34±0,003; у = 1,16±0,004.

3. Найдитезначение выражения:

4. Найти z₁ ± z_2, z₁z_2,z₁/z₂, если   z1=;   z2=

Вариант №7

1. Найти абсолютную и относительную погрешности если известно, что - 0,357 является приближенным значением для .

2. Найдите произведение чисел x = 21,35±0,003; у = 4,32±0,004.

3. Найдитезначение выражения:

4. Найти z₁ ± z_2, z₁z_2,z₁/z₂, если   z1= 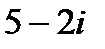; z2=

 

Вариант №8

1. Найти абсолютную и относительную погрешности если известно, что - 0,429 является приближенным значением для .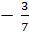

2. Найдите частное чисел x = 63,12±0,003; у = 5,26±0,004.

3. Найдитезначение выражения:

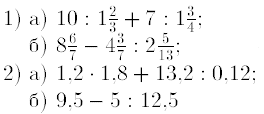
4. Найти z₁ ± z_2, z₁z_2, z₁/z₂, если   z1= -4-3i;    z2= -5i

Вариант №9

1. Найти абсолютную и относительную погрешности если известно, что 0,636 является приближенным значением для .

2. Найдите произведение чисел x = 34,16±0,003; у = 21,11±0,004.

3. Найдитезначение выражения:

4. Найти z₁ ± z_2, z₁z_2, z₁/z₂, если z1= 2+4i; z2= 5-5i

Вариант №10

1. Найти абсолютную и относительную погрешности если известно, что - 0,385 является приближенным значением для .

2. Найдите частное чисел x = 15,51±0,003; у = 18,28±0,004.

3. Найдитезначение выражения:

4. Найти z₁ ± z_2, z₁z_2, z₁/z₂, если   z1= -3+2i;   z2= 2+3i

 

Вариант №11

1. Найти абсолютную и относительную погрешности если известно, что 0,214 является приближенным значением для .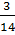

2. Найдите сумму и разность чисел x = 48,21±0,004; у = 5,16±0,005.

3. Найдитезначение выражения:

4. Найти z₁ ± z_2, z₁z_2, z₁/z₂, если   z1= 2+i; z2= 3-2i

 

Вариант №12

1. Найти абсолютную и относительную погрешности если известно, что - 0,571 является приближенным значением для .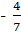

2. Найдите произведение чисел x = 36,85±0,004; у = 2,76±0,005.

3. Найдитезначение выражения:

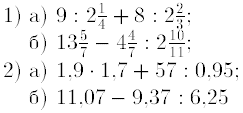
4. Найти z₁ ± z_2, z₁z_2, z₁/z₂, если   z1= 4-i; z2= 2-i

 

Вариант №13

1. Найти абсолютную и относительную погрешности если известно, что 0,545 является приближенным значением для .

2. Найдите частное чисел x = 54,29±0,004; у = 3,74±0,005.

3. Найдитезначение выражения:

4. Найти z₁ ± z_2, z₁z_2,z₁/z₂, если   z1=-16; z2= 1+i

 

Вариант №14

1. Найти абсолютную и относительную погрешности если известно, что - 0,462 является приближенным значением для .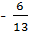

2. Найдите произведение чисел x = 48,16±0,004; у = 26,23±0,005.

3. Найдитезначение выражения:

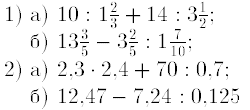
4. Найти z₁ ± z_2, z₁z_2, z₁/z₂, если   z1= 3+4i; z2= 4+3i

 

Вариант №15

1. Найти абсолютную и относительную погрешности если известно, что 0,071 является приближенным значением для .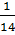

2. Найдите частное чисел x = 62,11±0,004; у = 32,54±0,005.

3. Найдитезначение выражения:

4. Найти z₁ ± z_2, z₁z_2, z₁/z₂, если   z1= -5i; z2= 2+I

Вариант №16

1. Найти абсолютную и относительную погрешности если известно, что - 0,714 является приближенным значением для .

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: