 |
Индивидуальные задания к практической работе №19
|
|
|
|
Вариант №1
1) 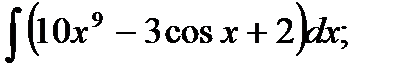 2) 2)  3)
3) 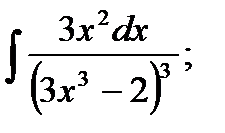 4) 4) 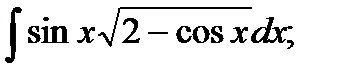 5)
5)  6* 6* 
| Вариант № 2
1)  2) 2)  3)
3)  4) 4) 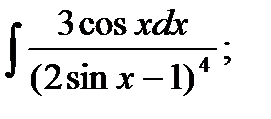 5)
5)  6* 6* 
|
Вариант №3
1)  2) 2)  3)
3) 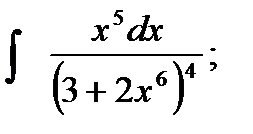 4) 4)  5)
5)  6* 6* 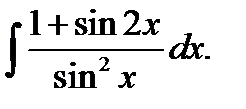
| Вариант №4
1)  2) 2) 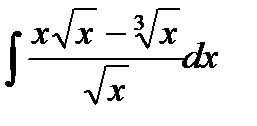 3)
3)  4) 4)  5)
5)  6* 6* 
|
Вариант №5
1) 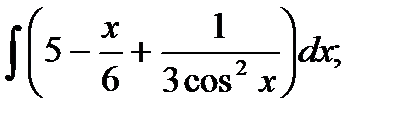 2) 2)  3)
3)  4) 4) 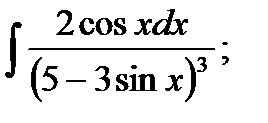 5)
5)  6* 6* 
| Вариант №6
1)  2) 2) 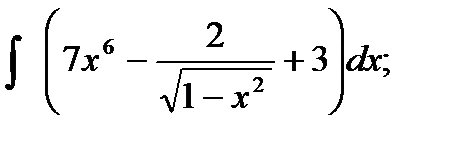 3)
3) 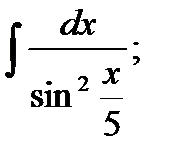 4) 4) 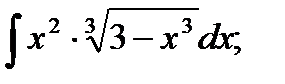 5)
5)  6* 6* 
|
Вариант №7
1)  2) 2) 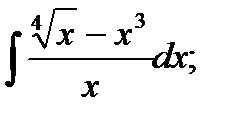 3)
3) 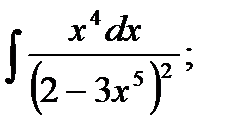 4) 4) 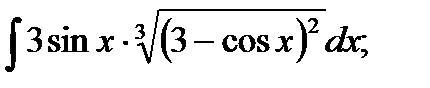 5)
5)  6* 6* 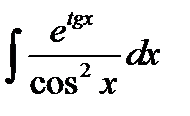
| Вариант №8
1) 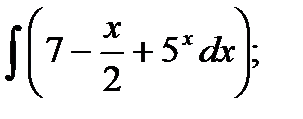 2) 2)  3)
3) 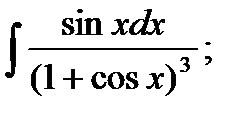 4) 4)  5)
5)  6* 6* 
|
Вариант №9
1) 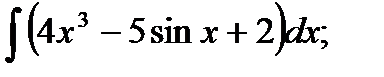 2) 2)  3)
3) 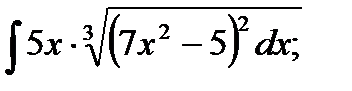 4) 4)  5)
5)  6* 6* 
| Вариант №10
1)  2) 2)  3)
3) 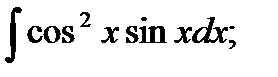 4) 4)   5)
5)  6* 6* 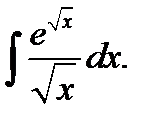
|
Вариант №11
1) 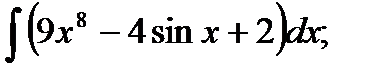 2) 2) 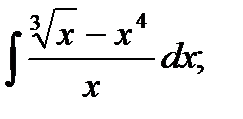 3)
3) 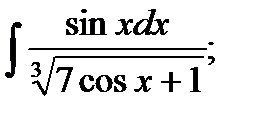 4) 4)  5)
5)  6* 6* 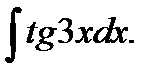
| Вариант №12
1)  2) 2)  3)
3)  4) 4)  5)
5) 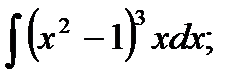 6* 6* 
|
Вариант №13
1)  2) 2) 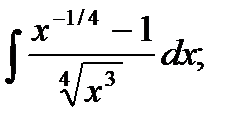 3)
3)  4) 4)  5)
5)  6* 6* 
| Вариант №14
1) 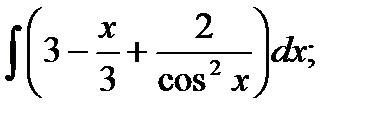 2) 2)  3)
3) 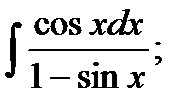 4) 4) 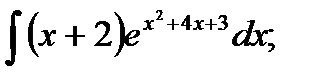 5)
5)  6* 6* 
|
Вариант №15
1)  2) 2) 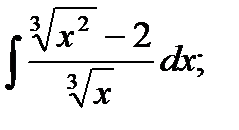 3)
3)  4) 4) 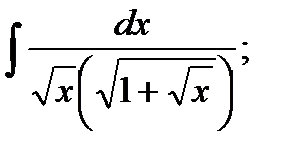 5)
5)  6* 6* 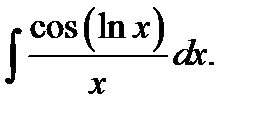
| Вариант №16
1) 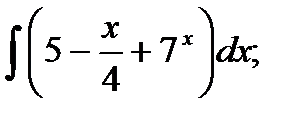 2) 2) 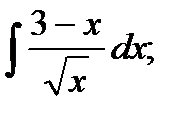 3)
3)  4) 4) 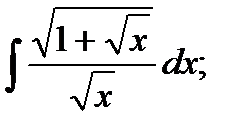 5)
5) 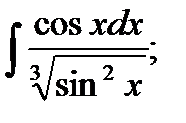 6* 6* 
|
Порядок выполнения практического задания:
1. Выполнить задания.
2. Ответить на вопросы для закрепления теоретического материала.
3. Оформить отчёт.
Содержание отчета: выполнить задания письменно на листах формата А4.
Контрольные вопросы:
8. Чему равна производная при данном значении аргумента с геометрической точки зрения?
9. Запишите уравнение касательной и нормали, проведенных через данную точку на кривой.
10. Как находится направление кривой в каждой ее точке?
11. Как вычисляется угловой коэффициент касательной в данной точке кривой?
12. Как определяется скорость изменения функции при данном значении аргумента?
|
|
|
13. Как определяется ускорение прямолинейного движения точки при данном значении аргумента?
14. Какие физические задачи решаются с применением производной?
15. Сформулируйте практическое правило исследования функции на возрастание и убывание.
16. Дайте определение максимума и минимума функции.
17. Приведите примеры функций, имеющих один максимум или минимум, множество максимумов и минимумов.
Список литературы
1 Башмаков М.И. Математика. Сборник задач профильной направленности М.: Академия Гриф 2013
2. Башмаков Н.А Математика М.: Академия Гриф 2011
3. www. fcior. edu. ru Информационные, тренировочные и контрольные материалы
4. www. school-collection. edu. Ru Единая коллекции цифровых образовательных ресурсов
Индивидуальные задания
Исследовать функции и построить их графики.
Вариант №1
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 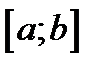
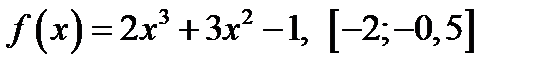 2. Точка движется прямолинейно по закону
2. Точка движется прямолинейно по закону  Найти значение скорости и ускорения в момент времени Найти значение скорости и ускорения в момент времени  3. Исследовать функцию и построить ее график. y=x3+6x2+9x;
4.Записать уравнение касательной к графику функции
3. Исследовать функцию и построить ее график. y=x3+6x2+9x;
4.Записать уравнение касательной к графику функции  в точке с абсциссой в точке с абсциссой 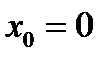 . .

| Вариант №2
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 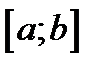
 2. Точка движется прямолинейно по закону
2. Точка движется прямолинейно по закону 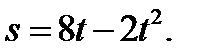 В какой момент времени скорость точки окажется равной нулю?
3. Исследовать функцию и построить ее график В какой момент времени скорость точки окажется равной нулю?
3. Исследовать функцию и построить ее график  ;
4.Записать уравнение касательной к графику функции ;
4.Записать уравнение касательной к графику функции  в точке с абсциссой в точке с абсциссой 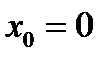 . .

| Вариант №3
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 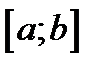
 2. Закон изменения температуры Т тела в зависимости от времени tзадан уравнением
2. Закон изменения температуры Т тела в зависимости от времени tзадан уравнением 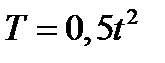 . С какой скоростью нагревается это тело в момент времени t =100?
3.Исследовать функцию и построить ее график. y=-x3+3x2-3;
4.Записать уравнение касательной к графику функции . С какой скоростью нагревается это тело в момент времени t =100?
3.Исследовать функцию и построить ее график. y=-x3+3x2-3;
4.Записать уравнение касательной к графику функции  в точке с абсциссой в точке с абсциссой 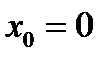 . .

|
Вариант №4
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 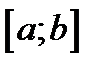
 2. Тело массой 100 кг движется прямолинейно по закону
2. Тело массой 100 кг движется прямолинейно по закону  Найти кинетическую энергию тела Найти кинетическую энергию тела  через 4с после начала движения.
3. Исследовать функцию и построить ее график. y=2+5x3-3x5;
4.Записать уравнение касательной к графику функции через 4с после начала движения.
3. Исследовать функцию и построить ее график. y=2+5x3-3x5;
4.Записать уравнение касательной к графику функции  . . 
| Вариант №5
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 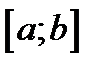
 2. Сила тока I изменяется в зависимости от времени закону
2. Сила тока I изменяется в зависимости от времени закону  (I – в амперах, t – в секундах). Найти скорость изменения силы тока в конце 8-й секунды.
3. Исследовать функцию и построить ее график (I – в амперах, t – в секундах). Найти скорость изменения силы тока в конце 8-й секунды.
3. Исследовать функцию и построить ее график  ;
4.Записать уравнение касательной к графику функции ;
4.Записать уравнение касательной к графику функции  . . 
| Вариант №6
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 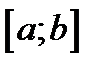
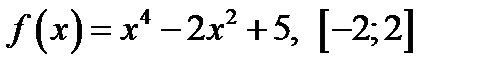 2. Найти скорость и ускорение в указанные моменты времени для точки, движущейся прямолинейно, если движение точки задано уравнением
2. Найти скорость и ускорение в указанные моменты времени для точки, движущейся прямолинейно, если движение точки задано уравнением
 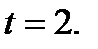 3. Исследовать функцию и построить ее график
3. Исследовать функцию и построить ее график  ;
4.Записать уравнение касательной к графику функции ;
4.Записать уравнение касательной к графику функции  . . 
|
Вариант №7
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 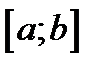
 2. Найти скорость и ускорение в указанные моменты времени для точки, движущейся прямолинейно, если движение точки задано уравнением
2. Найти скорость и ускорение в указанные моменты времени для точки, движущейся прямолинейно, если движение точки задано уравнением  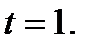 3. Исследовать функцию и построить ее график
3. Исследовать функцию и построить ее график 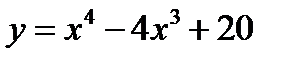 ;
4.Записать уравнение касательной к графику функции ;
4.Записать уравнение касательной к графику функции  . . 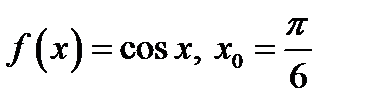
| Вариант №8
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 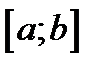
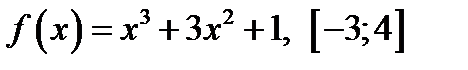 2. Найти скорость и ускорение в указанные моменты времени для точки, движущейся прямолинейно, если движение точки задано уравнением
2. Найти скорость и ускорение в указанные моменты времени для точки, движущейся прямолинейно, если движение точки задано уравнением 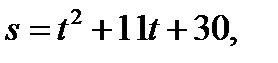  3. Исследовать функцию и построить ее график
3. Исследовать функцию и построить ее график 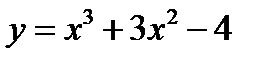 ;
4.Записать уравнение касательной к графику функции ;
4.Записать уравнение касательной к графику функции  . . 
| Вариант №9
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 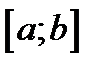
 2. Найдите ускорение точки в указанный момент времени, если скорость точки, движущейся прямолинейно, задана уравнением
2. Найдите ускорение точки в указанный момент времени, если скорость точки, движущейся прямолинейно, задана уравнением  , , 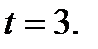 3.Исследовать функцию и построить ее график
3.Исследовать функцию и построить ее график 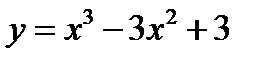 ;
4.Записать уравнение касательной к графику функции ;
4.Записать уравнение касательной к графику функции  . . 
|
Вариант №10
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 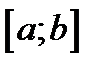
 2. Найдите ускорение точки в указанный момент времени, если скорость точки, движущейся прямолинейно, задана уравнением
2. Найдите ускорение точки в указанный момент времени, если скорость точки, движущейся прямолинейно, задана уравнением 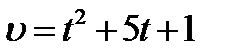 , , 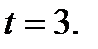 3.Исследовать функцию и построить ее график. y=2+3x-x3;
4.Записать уравнение касательной к графику функции
3.Исследовать функцию и построить ее график. y=2+3x-x3;
4.Записать уравнение касательной к графику функции  . .

| Вариант №11
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 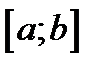
 2. Точка движется прямолинейно по закону
2. Точка движется прямолинейно по закону 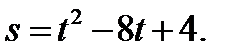 В какой момент времени скорость точки окажется равной нулю?
3.Исследовать функцию и построить ее график. y=x3-x2-x-1;
4.Записать уравнение касательной к графику функции В какой момент времени скорость точки окажется равной нулю?
3.Исследовать функцию и построить ее график. y=x3-x2-x-1;
4.Записать уравнение касательной к графику функции  в точке с абсциссой в точке с абсциссой 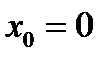 . . 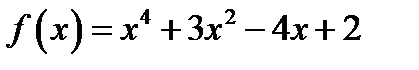
| Вариант №12
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 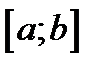
 2. Температура тела Т изменяется в зависимости от времени t по закону
2. Температура тела Т изменяется в зависимости от времени t по закону  С какой скоростью нагревается это тело в момент времени t=5?
3.Исследовать функцию и построить ее график С какой скоростью нагревается это тело в момент времени t=5?
3.Исследовать функцию и построить ее график 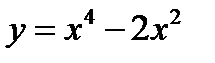 ;
4.Записать уравнение касательной к графику функции ;
4.Записать уравнение касательной к графику функции  в точке с абсциссой в точке с абсциссой 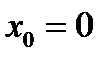 . . 
|
Вариант №13
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 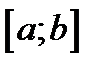
 2. Изменение силы тока I в зависимости от времени t дано уравнением
2. Изменение силы тока I в зависимости от времени t дано уравнением 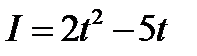 (I – в амперах, t – в секундах). Найдите скорость изменения силы тока в конце 10-й секунды.
3.Исследовать функцию и построить ее график (I – в амперах, t – в секундах). Найдите скорость изменения силы тока в конце 10-й секунды.
3.Исследовать функцию и построить ее график  4.Записать уравнение касательной к графику функции
4.Записать уравнение касательной к графику функции  в точке с абсциссой в точке с абсциссой 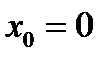 . . 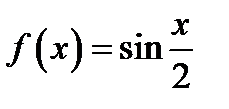
| Вариант №14
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 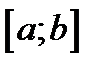
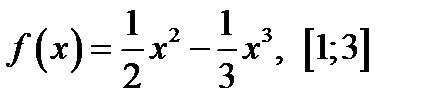 2. Найти скорость и ускорение в указанные моменты времени для точки, движущейся прямолинейно, если движение точки задано уравнением
2. Найти скорость и ускорение в указанные моменты времени для точки, движущейся прямолинейно, если движение точки задано уравнением  3.Исследовать функцию и построить ее график
3.Исследовать функцию и построить ее график  ;
4.Записать уравнение касательной к графику функции ;
4.Записать уравнение касательной к графику функции  . .

| Вариант №15
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 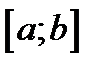
 2. Тело массой 100 кг движется прямолинейно по закону
2. Тело массой 100 кг движется прямолинейно по закону 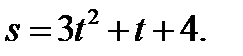 Найти кинетическую энергию тела Найти кинетическую энергию тела  через 4с после начала движения.
3.Исследовать функцию и построить ее график через 4с после начала движения.
3.Исследовать функцию и построить ее график  ;
4.Записать уравнение касательной к графику функции ;
4.Записать уравнение касательной к графику функции  . .

|
Вариант №16
1. Найти наибольшее и наименьшее значение функции  на отрезке на отрезке 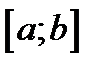
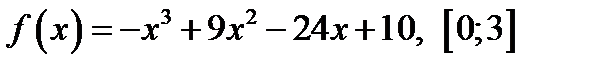 2. Точка движется прямолинейно по закону
2. Точка движется прямолинейно по закону 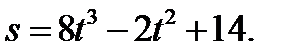 Найти значение скорости и ускорения в момент времени Найти значение скорости и ускорения в момент времени  3.Исследовать функцию и построить ее график.
3.Исследовать функцию и построить ее график.
 ;
4.Записать уравнение касательной к графику функции ;
4.Записать уравнение касательной к графику функции  . . 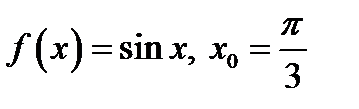
| ||
|
|
|
|
|
|
Практическое занятие №19
«Вычисление площадей плоских фигур с помощью определенного интеграла»
|
|
|
Практическое занятие рассчитано на 2 часа, относится к теме «Первообразная и интеграл».
Формируемые компетенции: У13, У14,У19,З1, З2, З3
Цель: научиться решать задачи на вычисление площадей плоских фигур, используя определённый интеграл.
Методическое и техническое обеспечение:
- методические указания к выполнению практического занятия;
- комплекты учебно-наглядных пособий по соответствующим разделам математики.
- мультимедийный проектор;
- ноутбук;
- проекционный экран;
- компьютерная техника для обучающихся с наличием лицензионного программного обеспечения;
- комплект слайд-презентаций.
Теоретические сведения
Геометрический смысл определённого интеграла S= 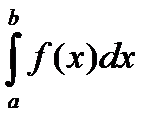 :
:
Площадь фигуры, ограниченной функциями y=f(x),y=0, x=a, x=b, равна определённому интегралу от функции f(x) на отрезке [a; b]
| у |
| 0 |
| а |
| б |

|
| у |
| 0 |
| а |
| б |
| х |
| х |
y= 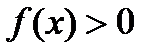
S
S
S= 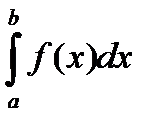 (1) S=
(1) S=  (2)
(2)
| y1=f(x) S |
| 0 |
| а |
| б |
| х |
y=f(x)
a 0 bx y 2 = g (x)
S =  (3) S =
(3) S =  (4)
(4)
Вычисление объёмов фигур вращения определяется формулами:
| х |
| б |
| а |
y=f(x) вращение плоской фигуры вокруг оси OX
V=  (5)
(5)
| d |
| с |
| 0 |
| х |
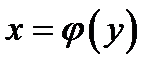
|
- вращение плоской фигуры вокруг оси OY
V= 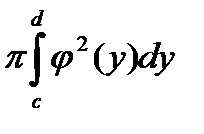 (6)
(6)
Замечание. При вычислении площади плоской фигуры или объёма тела вращения необходимо
1) сделать схематический чертёж фигуры, решив систему уравнений;
2) найти отрезок интегрирования;
3) верно выбрать формулу для вычисления площади или объёма.
Пример выполнения задания
Пример №1. Дано: x+2y-4=0, y=0, x=-3, x=2.
Найти площадь фигуры, ограниченной этими линиями.
| S |
| -3 |
| 0 |
| 2 |
| х |
| у=0,5х+2 |
y=-0.5 x+2
| х | 0 | 4 |
| у | 2 | 0 |
2) у=0 – ось ОХ;
3) х=-3 и х=2 – прямые параллельные OY.
По формуле (1) находим
S= 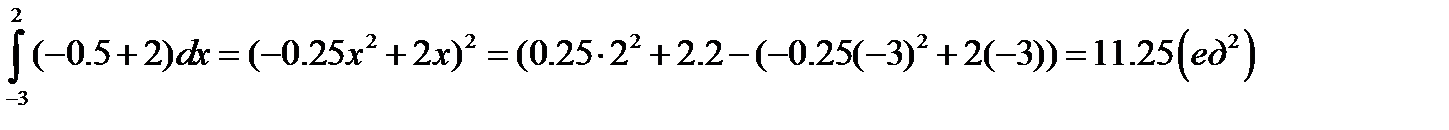
Ответ: S=11,25 ед2.
Пример №2. Дано: y= 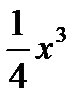 , y=0, x=-1, x=2. Найти площадь фигуры, ограниченной этими линиями.
, y=0, x=-1, x=2. Найти площадь фигуры, ограниченной этими линиями.
| у |
| у=х3/4 |
| х |
| 2 |
| 0 |
| -1 |
y= (1/4)x3 –кубическая парабола,
y=0 – ось ОX,
x=-1, x=2-прямые параллельные OY
|
|
|
Согласно формуле (3) S= 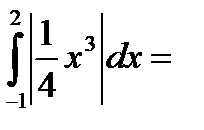
= 
Ответ: S=  .
.
Пример №3 Дано: y=x2; y=2x; Найти площадь фигуры, ограниченной этими линиями.
Решение:
| у=х2 |
| 2 |
| х |
| 0 |
| у=2х |
| у |
y=x2 – парабола;
y=2x- прямая
| х | 0 | 1 |
| у | 0 | 1 |
Найдем абсциссы точек пересечения графиков функций

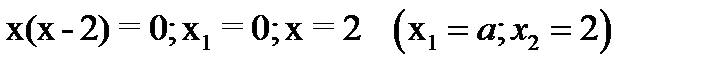
Применяя формулу (4), находим
S= 
Ответ: 
Порядок выполнения практического задания:
1. Выполнить задания.
2. Ответить на вопросы для закрепления теоретического материала.
3. Оформить отчёт.
Содержание отчета: выполнить задания письменно на листах формата А4.
Контрольные вопросы:
1. Выпишите формулы Ньютона – Лейбница и объясните ее смысл.
2. Приведите основные свойства определенного интеграла.
3. Объясните, в чем заключается геометрический смысл определенного интеграла.
4. В чем заключается соответствие между пределом интегральной суммы и определенным интегралом?
Список литературы
1 Башмаков М.И. Математика. Сборник задач профильной направленности М.: Академия Гриф 2013
2. Башмаков Н.А Математика М.: Академия Гриф 2011
3. www. fcior. edu. ru Информационные, тренировочные и контрольные материалы
4. www. school-collection. edu. Ru Единая коллекции цифровых образовательных ресурсов
Индивидуальные задания
Найти площади фигур, ограниченных линиями.
В.1
№1
В. 9
№1
В. 2
№1
В.1 0
№1
В. 3
№1
В.1 1
№1
В. 4
№1
В.1 2
№1
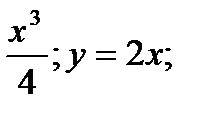
В. 5
№1
В.1 3
№1
 x2+3; y=0
x2+3; y=0
В.6
№1
В.1 4
№1
В.7
№1
 y=-x2+6x-5
y=-x2+6x-5
В.1 5
№1
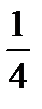 x2; y=-1/2 x2+3x
x2; y=-1/2 x2+3x
В.8
№1
В.1 6
№1
 ; y=0; x=0; x=3;
; y=0; x=0; x=3;


