 |
Практическое занятие №5«Выполнение тождественных преобразований в тригонометрических выражениях» 3 глава
|
|
|
|
2. Найдите сумму и разность чисел x = 29,41±0,005; у = 6,28±0,006.
3. Найдитезначение выражения:
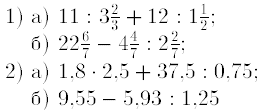
4. Найти z1 ± z2, z1z2, z1/z2, если z1= 4-i; z2= 2-i
Вариант №17
1. Найти абсолютную и относительную погрешности если известно, что 0,455 является приближенным значением для  .
.
2. Найдите произведение чисел x = 52,47±0,005; у = 3,54±0,006.
3. Найдитезначение выражения:
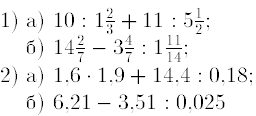
4. Найти z1 ± z2, z1z2, z1/z2, если z1=2+2i; z2=2+i
Практическое занятие №3
«Выполнение тождественных преобразований над степенными выражениями»
Практическое занятие рассчитано на 2 часа, относится к теме «Корни, степени и логарифмы».
Формируемые компетенции: У2, У3, У4, З1, З2, З3
Цель: Научиться выполнять тождественные преобразования в степенных выражениях, используя формулы сокращённого умножения.
Методическое и техническое обеспечение:
- методические указания к выполнению практического занятия;
- комплекты учебно-наглядных пособий по соответствующим разделам математики.
- мультимедийный проектор;
- ноутбук;
- проекционный экран;
- компьютерная техника для обучающихся с наличием лицензионного программного обеспечения;
- комплект слайд-презентаций.
Теоретические сведения
I. Свойства степеней
Определение: Пусть дано положительное число a и произвольное рациональное число n. Число an называется степенью, число a - основанием степени, число n - показателем степени. По определению полагают:
· 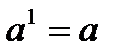
· 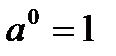
Частные случаи:
· 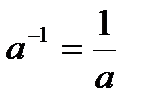
· 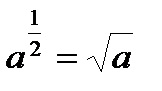
· 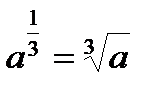
· 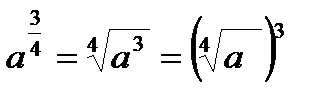
II. Свойства степени с рациональным показателем и квадратного (арифметического) корня
При решении задач на выполнение арифметических действий, прежде всего, следует обратить внимание на форму представления чисел и порядок действий. Полезно потренироваться в переходе от десятичных к обыкновенным дробям и обратно, в переходе от смешанных чисел к дробям и обратно. В процессе вычислений полезно сначала максимально упростить арифметическое выражение, выбрав подходящее представление чисел, освободиться от степеней с отрицательными показателями и т. п.
|
|
|
Напомним свойства степеней и действия с корнями:
1. 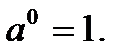
2. 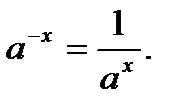
3. 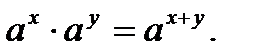
4. 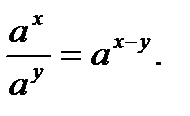
5. 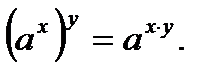
6. 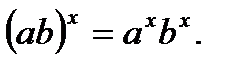
7. 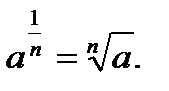
8. 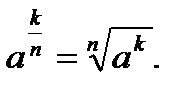
9. 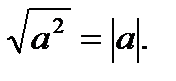
10. 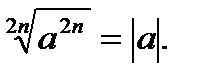
11. 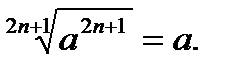
12. 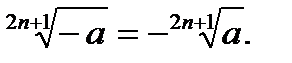
13. 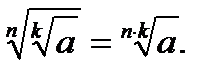
14. 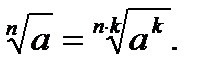
15. 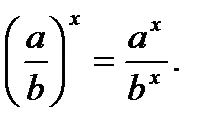
16. 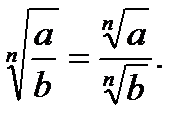
17. 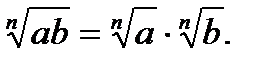
18. 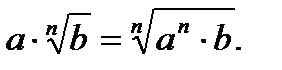
Формулы сокращенного умножения:
1. 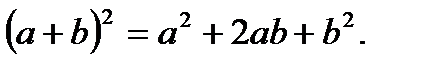
2. 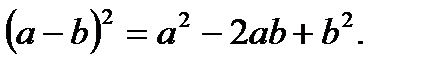
3. 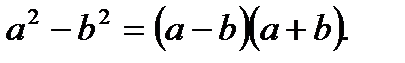
4. 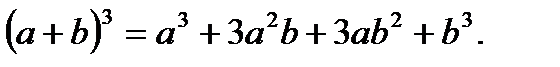
5. 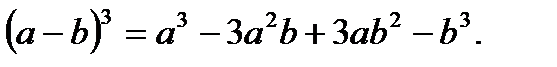
6. 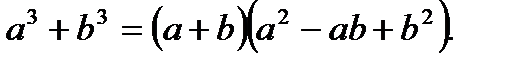
7. 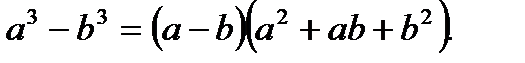
При решении задач часто необходимо освободиться от иррациональности в знаменателе дроби. Для этого применяют следующие формулы:
8. 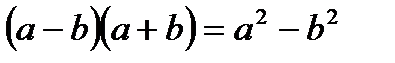 ;
;
9. 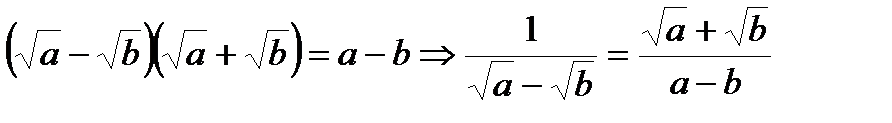 , или
, или  ;
;
10. 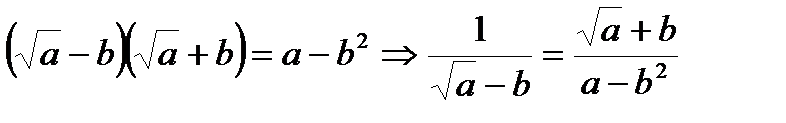 , или
, или 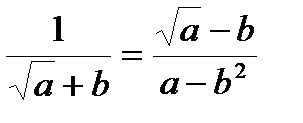 ;
;
11. 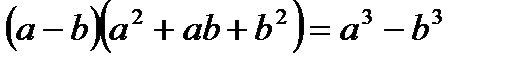 ;
;
12. 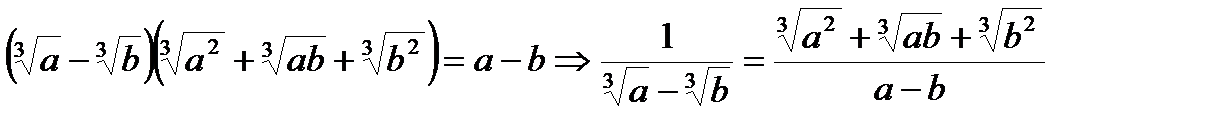 ;
;
13. 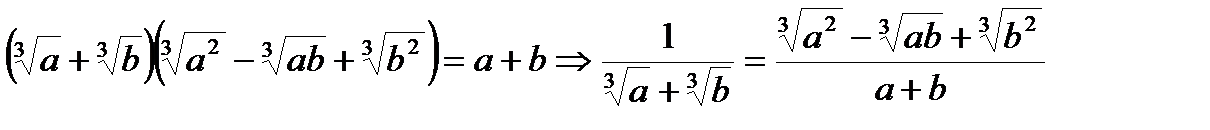 ;
;
14. 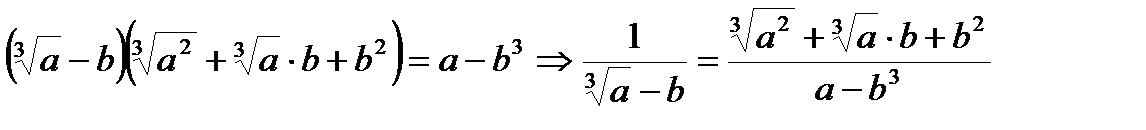 ;
;
15. 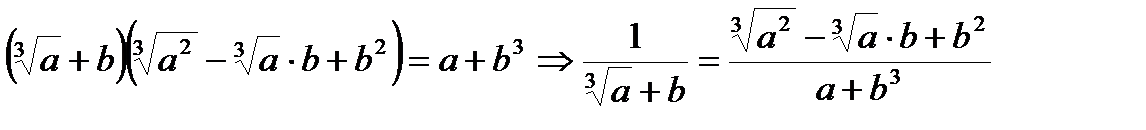 .
.
Пример выполнения задания
Пример №1. Вычислить: а)  ; б)
; б) 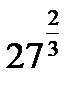 ; в)
; в) 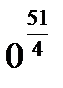 ; г)
; г) 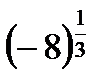 .
.
Решение. 1) 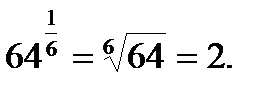
2) 
3) 
4) Это задание некорректно, поскольку нет определения степени с дробным показателем для случая отрицательного основания. Математики договорились возводить в дробные степени только неотрицательные числа (и это оговорено в определении). Так что запись вида 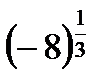 считается в математике лишённой смысла.
считается в математике лишённой смысла.
Пример №2:

Пример №3. Упростить выражение: 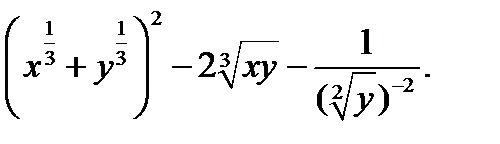
Решение:
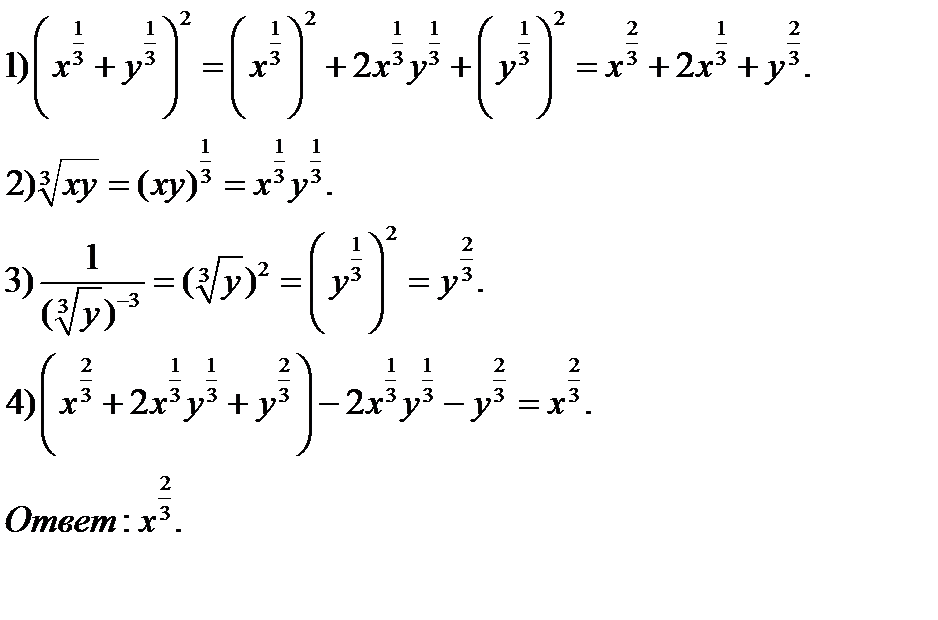
Пример №4. Найдем значение выражения 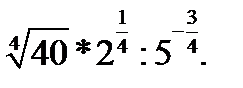

Пример №5. Преобразуем выражения:
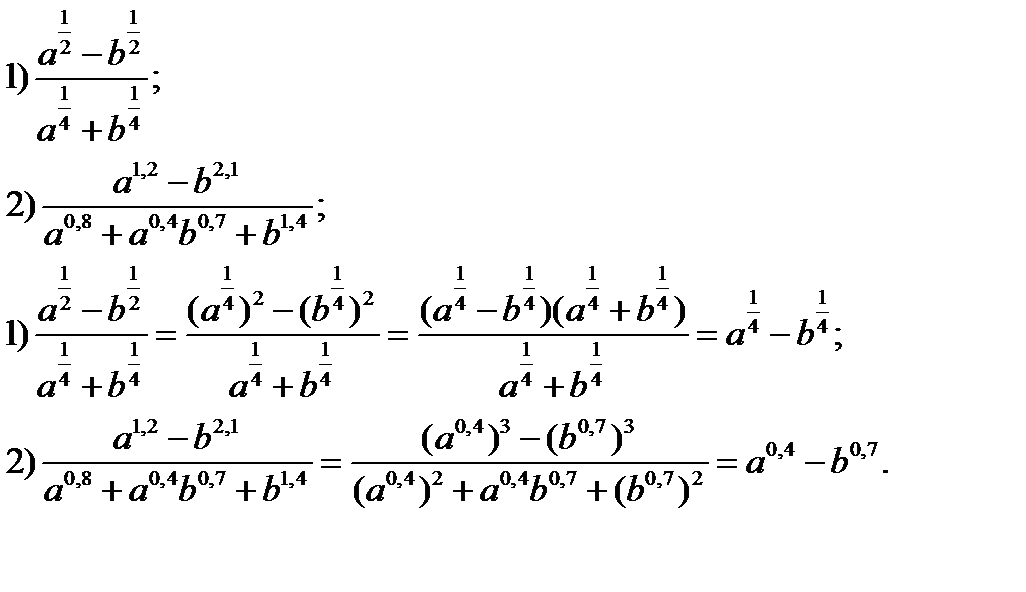
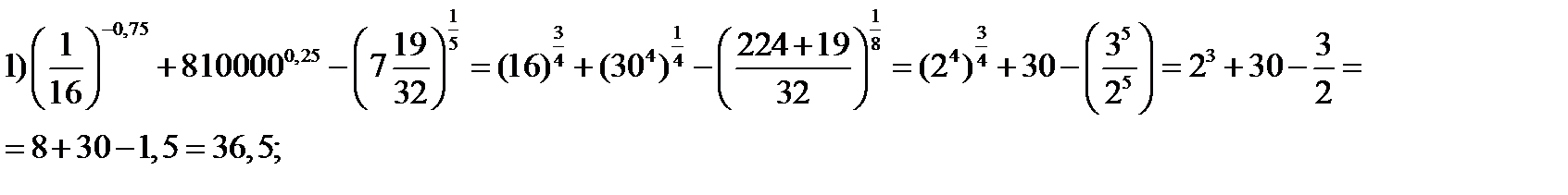
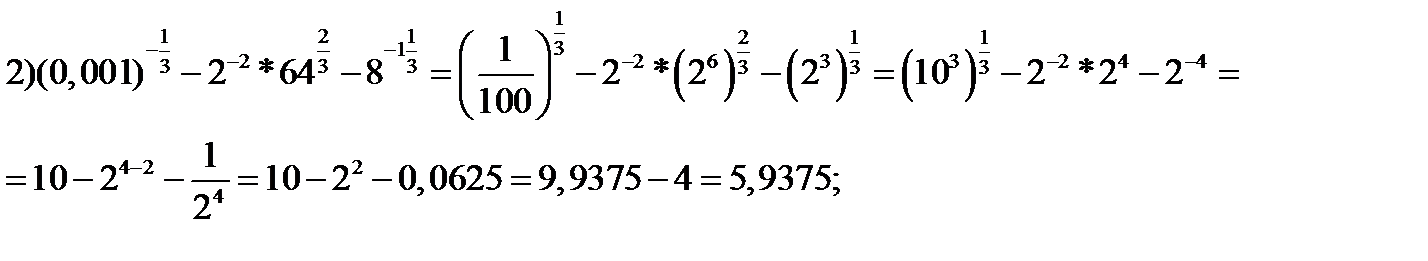
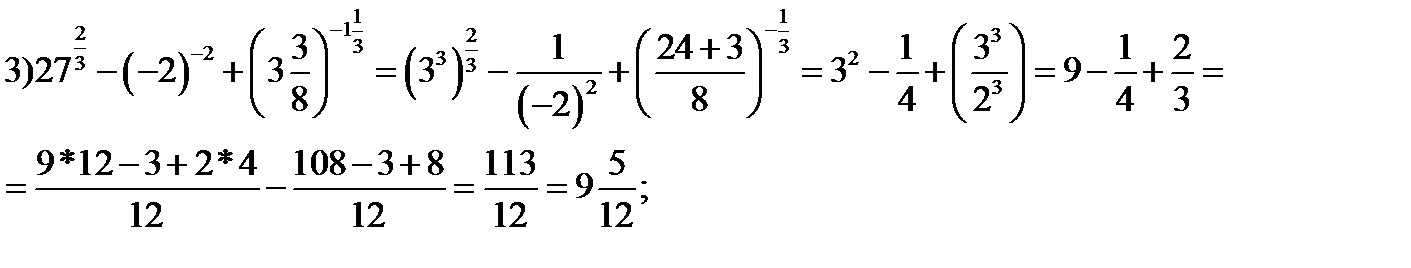
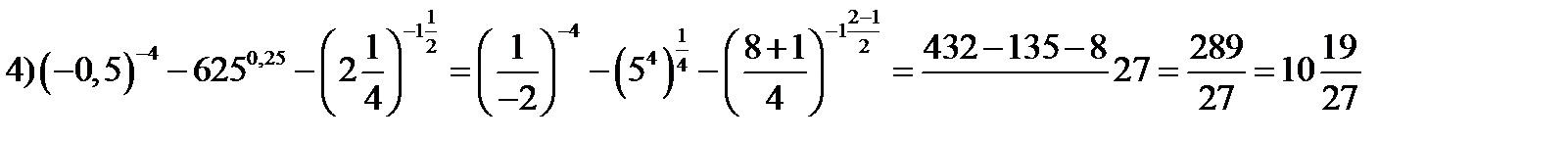
Порядок выполнения практического задания:
1. Выполнить задания.
2. Ответить на вопросы для закрепления теоретического материала.
3. Оформить отчёт.
Содержание отчета: выполнить задания письменно на листах формата А4.
Контрольные вопросы:
1. Что называется степенью с натуральным показателем?
2. Как умножить 2 степени с одинаковыми основаниями?
3. Как разделить 2 степени с одинаковыми основаниями?
4. Как возвести степень в степень?
5. Дайте определение числа с нулевым показателем.
6. Сформулируйте правило возведения в степень произведения.
7. Сформулируйте правило возведения дроби в степень.
8. Как возвести в четную степень отрицательное число?
9. Как возвести в нечетную степень отрицательное число?
|
|
|
10. Понятие корня натуральной степени из числа и его свойства
11. Понятие степени с рациональным показателем. Свойства степени с рациональными показателем
12. Понятие степени с действительным показателем
Список литературы
1 Башмаков М.И. Математика. Сборник задач профильной направленности М.: Академия Гриф 2013
2. Башмаков Н.А Математика М.: Академия Гриф 2011
3. www. fcior. edu. ru Информационные, тренировочные и контрольные материалы
4. www. school-collection. edu. Ru Единая коллекции цифровых образовательных ресурсов
Индивидуальные задания
| Вариант№1 | Вариант№2 | Вариант№3 |
   
| 
|

|
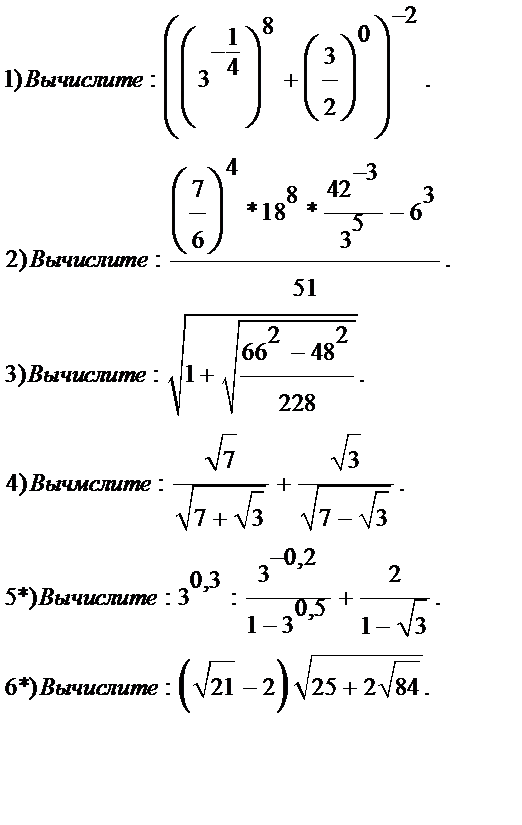
| Вариант№4 | Вариант№5 | Вариант№6 |

| 
| 
|
| Вариант№7 | Вариант№8 | Вариант№9 |
 
|

| 
|
| Вариант№10 | Вариант№11 | Вариант№12 |
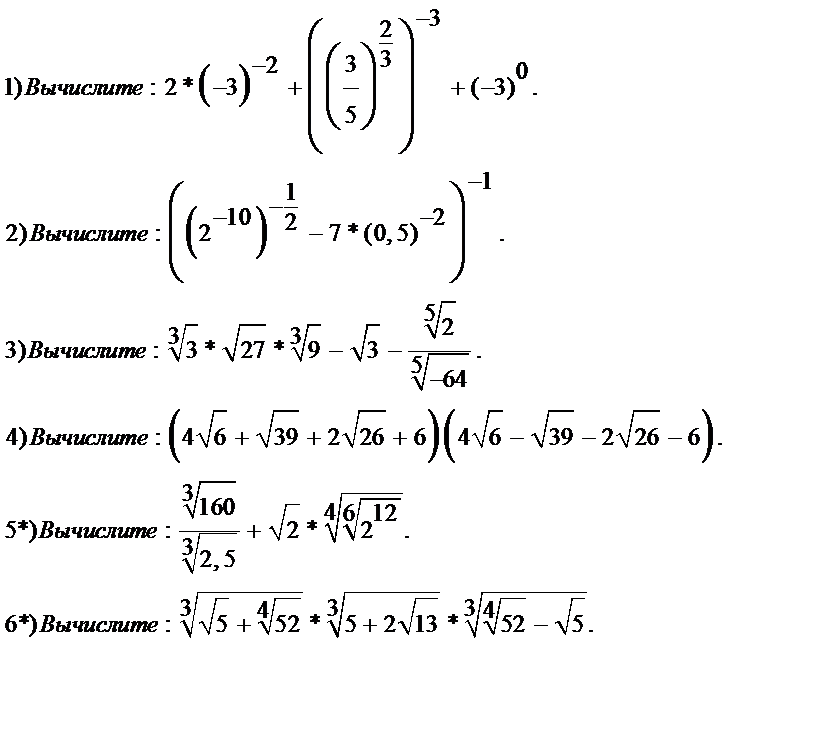
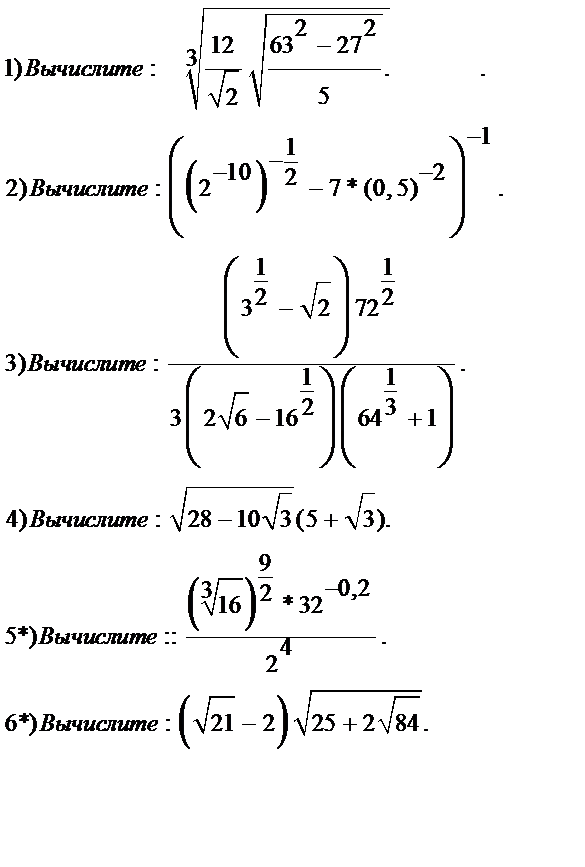
| 
| 
|
| Вариант№13 | Вариант№14 | Вариант№15 |

| 
| 
|
| Вариант№16 | ||

| ||
Практическое занятие №4
«Преобразование и вычисление значений логарифмических выражений»
Практическое занятие рассчитано на 2 часа, относится к теме «Корни, степени и логарифмы».
Формируемые компетенции: У2, У3, У4, З1, З2, З3
Цель: научиться вычислять и преобразовывать значения логарифмических выражений.
Методическое и техническое обеспечение:
- методические указания к выполнению практического занятия;
- комплекты учебно-наглядных пособий по соответствующим разделам математики.
- мультимедийный проектор;
- ноутбук;
- проекционный экран;
- компьютерная техника для обучающихся с наличием лицензионного программного обеспечения;
- комплект слайд-презентаций.
Теоретические сведения
Логарифмом числа «b» по основанию «а» называется показатель степени (с), в которую нужно возвести число «а», чтобы получить число «b» 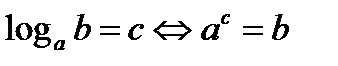 , где
, где 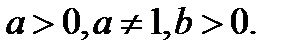
Например: 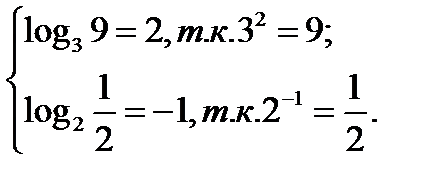
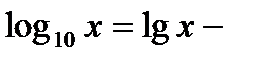 десятичный логарифм,
десятичный логарифм,
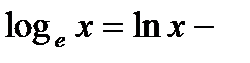 натуральный логарифм, где
натуральный логарифм, где 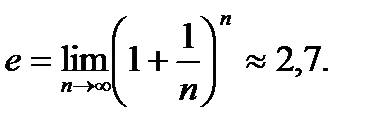
Свойства логарифма
1. 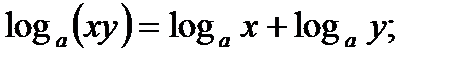
2. 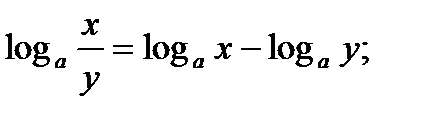
3. 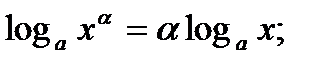
4. 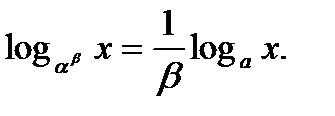
5. 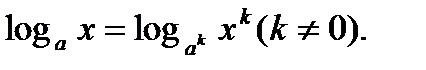
6. 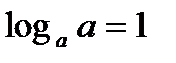 ,
, 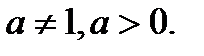
7. 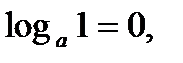
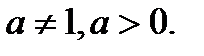
Основное логарифмическое тождество: 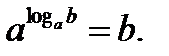
Формулы перехода от одного основания логарифма к другому:
1.  ,
, 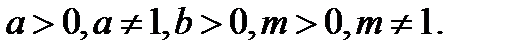
2. 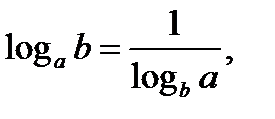
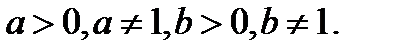
Если некоторое выражение А составлено из положительных чисел с помощью операций умножения, деления и возведения в степень, то, используя свойства логарифмов, можно выразить 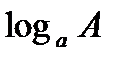 через логарифмы входящих в выражение А чисел. Такое преобразование называется логарифмированием.
через логарифмы входящих в выражение А чисел. Такое преобразование называется логарифмированием.
|
|
|
Часто приходится решать обратную задачу: находить выражение, логарифм которого представлен через логарифмы некоторых чисел. Такое преобразование называется потенцированием.
Пример выполнения задания
Пример №1. Вычислить 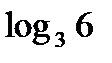 , если известно, что
, если известно, что 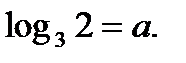
Решение. Используя свойство 1, имеем 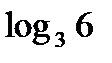 =
= 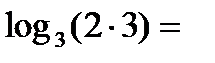
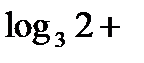
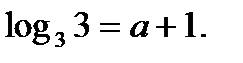
Пример №2. Вычислить 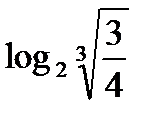 , если
, если 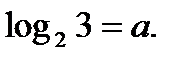
Решение. Используя свойства 2 и 3, находим 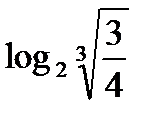 =
= 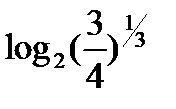 =
= 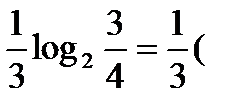
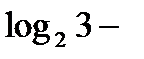
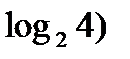 =
= 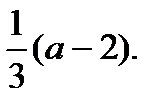
Пример №3. Вычислить 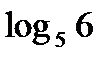 , если
, если 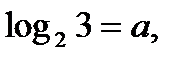

Решение. Перейдем в 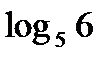 к основанию 2.Воспользовавшись свойством 4,а затем свойствами 1 и 2,получим
к основанию 2.Воспользовавшись свойством 4,а затем свойствами 1 и 2,получим 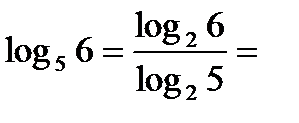
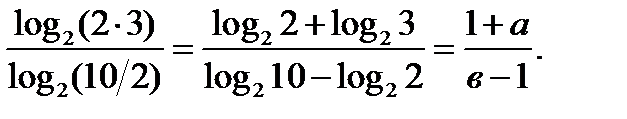
Пример №4. Вычислить 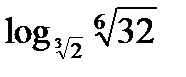 .
.
Решение. Согласно свойству 5, основание логарифма и логарифмируемое число можно возвести в одну и ту же степень. Следовательно, 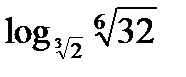 =
= 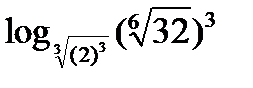 =
= 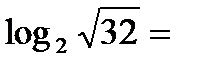
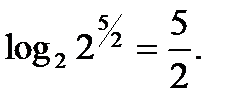
Пример №5. Вычислить 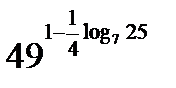 .
.
Решение. Имеем 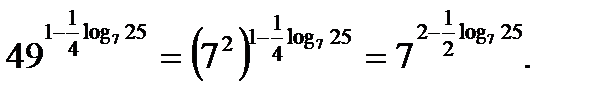
Преобразуем показатель полученной степени:
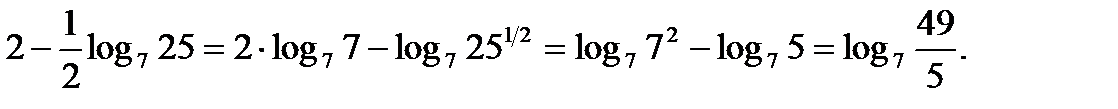
Таким образом, 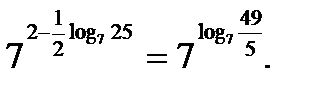 Из определения логарифма (тождество 1) следует, что
Из определения логарифма (тождество 1) следует, что 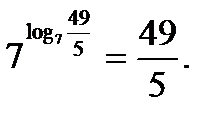
Пример №6. Найти значение выражения 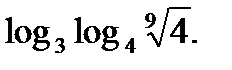
Решение. Согласно свойству логарифмов 3 имеем
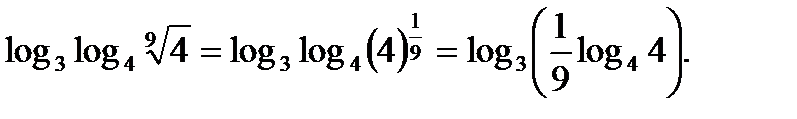
По свойству логарифмов 6 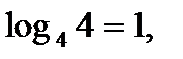 т.е. получим
т.е. получим

Используя свойства логарифмов 3 и 6,имеем
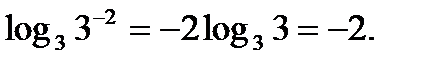
Пример №7. Найти значение выражения 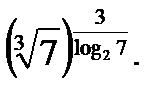
Решение. Используя тождество 2, перейдем в показателе степени к логарифму по основанию 7
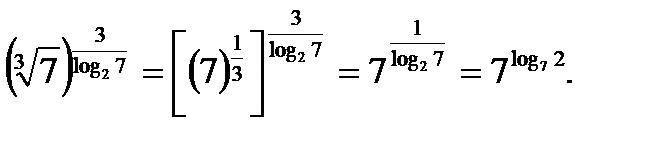
По основному логарифмическому тождеству последнее выражение равно 2.
Пример №8. Прологарифмировать по основанию 5 выражение 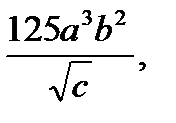 где a,b,c-положительные числа.
где a,b,c-положительные числа.
Решение. Используя свойства 1-3 логарифмов, получим
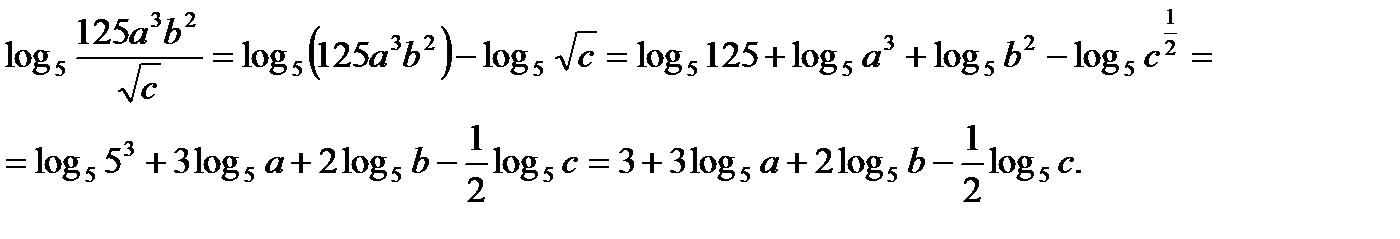
Пример №9. Найти x(пропотенцировать), если 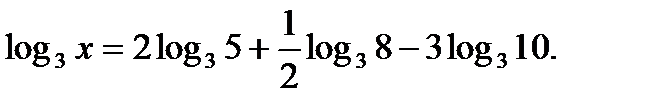
Решение. Имеем
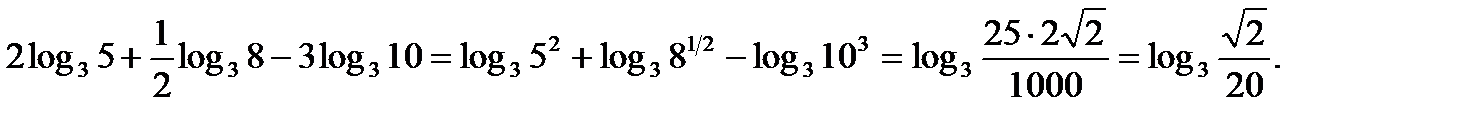
Из равенства 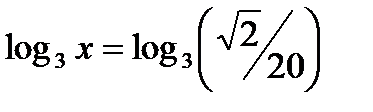 находим, что
находим, что 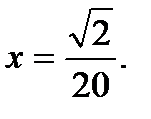
Порядок выполнения практического задания:
1. Выполнить задания.
2. Ответить на вопросы для закрепления теоретического материала.
3. Оформить отчёт.
Содержание отчета: выполнить задания письменно на листах формата А4.
Контрольные вопросы:
1. Перечислите основные свойства логарифмической функции при а>1 и при 0<а<1.
2. Сформулируйте основное логарифмическое тождество.
3. Перечислите основные свойства логарифмов.
4. Приведите доказательства логарифмических тождеств.
5. Приведите определение логарифма числа по данному основанию.
6. Как связаны между собой графики показательной и логарифмической функций?
|
|
|
Список литературы
1 Башмаков М.И. Математика. Сборник задач профильной направленности М.: Академия Гриф 2013
2. Башмаков Н.А Математика М.: Академия Гриф 2011
3. www. fcior. edu. ru Информационные, тренировочные и контрольные материалы
4. www. school-collection. edu. Ru Единая коллекции цифровых образовательных ресурсов
Индивидуальные задания
Вариант 1.
1. Найдите: а) 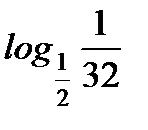 ; б)
; б) 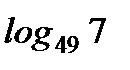 .
.
2. С помощью основного логарифмического тождества вычислите: 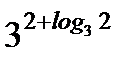 .
.
3. Прологарифмируйте по основанию 2 выражение 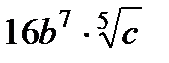
 .
.
4. Найдите х, если 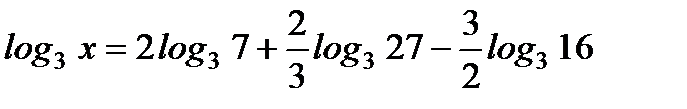 .
.
Вариант 2.
1. Найдите: а) 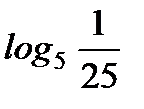 ; б)
; б) 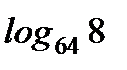 .
.
2. С помощью основного логарифмического тождества вычислите: 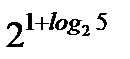 .
.
3. Прологарифмируйте по основанию 10 выражение 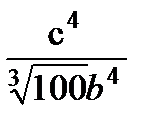
 .
.
4. Найдите х, если 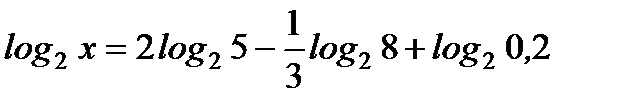 .
.
Вариант 3.
1. Найдите: а) 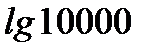 ; б)
; б) 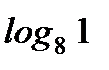 .
.
2. С помощью основного логарифмического тождества вычислите: 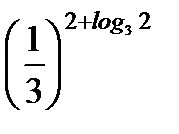 .
.
3. Прологарифмируйте по основанию 3 выражение 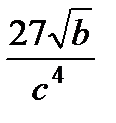
 .
.
4. Найдите х, если 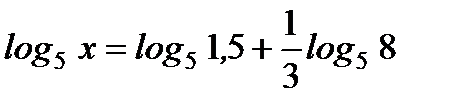 .
.
Вариант 4.
1. Найдите: а) 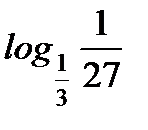 ; б)
; б) 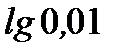 .
.
2. С помощью основного логарифмического тождества вычислите: 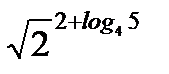 .
.
3. Прологарифмируйте по основанию 0,7 выражение 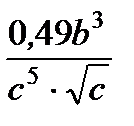
 .
.
4. Найдите х, если 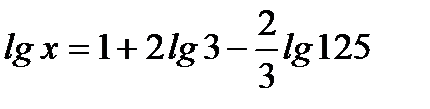 .
.
Вариант 5.
1. Найдите: а) 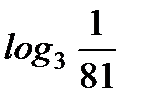 ; б)
; б) 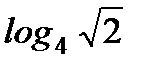 .
.
2. С помощью основного логарифмического тождества вычислите: 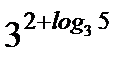 .
.
3. Прологарифмируйте по основанию 5 выражение 
 .
.
4. Найдите х, если 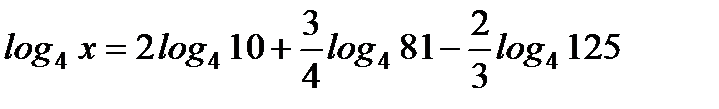 .
.
Вариант 6.
1. Найдите: а) 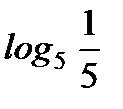 ; б)
; б) 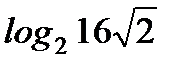 .
.
2. С помощью основного логарифмического тождества вычислите: 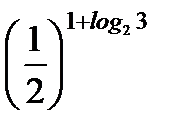 .
.
3. Прологарифмируйте по основанию 0,2 выражение 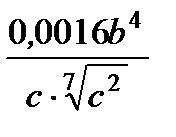
 .
.
4. Найдите х, если 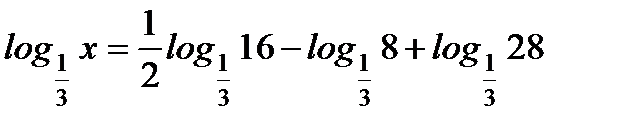 .
.
|
|
|


