Моделирование колебательных систем

ЛАБОРАТОРНАЯ РАБОТА №1

ВВЕДЕНИЕ В Simulink

 

Цель работы:

Ознакомиться с системой математического моделирования MATLAB/Simulink.

 

Краткие сведения о пакете

Система структурного моделирования Simulink предназначена для компьютерной реализации математических моделей динамических систем и устройств, представленных функциональной блок-схемой или системой уравнений. При этом возможны различные варианты моделирования: во временной области, в частотной области, с событийным управлением и т.д.

Для построения функциональной блок-схемы моделируемых устройств Simulink имеет обширную библиотеку блочных компонентов и удобный редактор блок-схем. Он основан на графическом интерфейсе пользователя и по существу является типичным средством визуально-ориентированного программирования. Используя библиотеку компонентов решающих блоков, пользователь с помощью мыши переносит нужные блоки из библиотеки в рабочее окно пакета Simulink и соединяет линиями связи входы и выходы блоков. Таким образом, создается блок-схема системы или устройства, то есть компьютерная модель.

Порядок работы с пакетом Simulink следующий:

1 На рабочем столе открываем пиктограмму MATLAB.

2 В открывшемся командном окне на панели инструментов нажимаем кнопку Simulink.

3 Открывается Simulink. Кроме рабочего окна с общим именем Untitled (“Безымянный”) открывается окно библиотеки Simulink с разделами:

- Sourses – источники;

- Sinks – приемники;

- Discrete – дискретные;

- Linear – линейные;

- Nonlinear – нелинейные

- Connections – связи;

- и т.д.

 

Разработано совместно с асс. Радченко В.П.

 

 

Порядок выполнения работы:

В качестве примера рассмотрим демонстративный пример. Для этого:

1. Нажимаем кнопку Demos в меню Help.

2. В левом окошке выбираем пункт Simulink.

3. Двойным щелчком выбираем пункт Simple models (в версии 6.1 и выше пункт General).

4. В правом окне выбираем модель Spring-mass system simulation.

5. Запускаем ее командой Run или двойным щелчком.

 

 

Рисунок 1.1 - Окно Демонстрации “Spring–mass system simulation”

 

Данная модель реализует колебательную механическую систему с одной степенью свободы. Физическим аналогом модели является переменное по направлению движение, закрепленной пружиной к “прыгающей” заделке (слева) массы по гладкой поверхности с трением. Внешняя сила приложена к заделке. Модель реализует дифференциальное уравнение, описывающее движение кубика. В MATLAB в передаточных функциях вместо p – оператора Лапласа пишется s.

Рассмотрим блоки (слева направо):

Input – генератор, x1 – звено первого порядка, сумматор, усилитель, 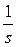– интегратор, Mux - смеситель (позволяет вывести более одного сигнала на Scope), Scope (Actual position) – осциллограф, Animation function - блок анимации.

Запуск моделирования осуществляется кнопкой .

На экране – анимационная картинка, представленная на рис. 1.2:

 

 

Рисунок 1.2 - Движение груза на пружине

 

Двойной щелчок на Scope после запуска моделирования открывает окно Scope (рис. 1.3), в котором отображаются графики, характеризующие колебания правой массы во времени и знакопеременную внешнюю силу.

Остановить моделирование с помощью значка и закрыть окна демонстрации.

 

 

Рисунок 1.3 - Графики, характеризующие работу системы

Ход работы:

1. На экране – открыть окно библиотеки и рабочее окно Simulink.

2. В окне библиотеки двойным щелчком раскрывается каждый из разделов. В разделе библиотеки Sourсes (Источники) выбираем генератор Signal Generator, перетаскиваем его в рабочее окно и закрываем окно Sourсes.

3. В разделе Sinks ( Приемники) выбираем осциллограф Scope, перетаскиваем в рабочее окно и закрываем окно Sinks.

4. В разделе Linear (Линейные блоки) или Math (для версии 6.1 и выше) выбираем блок усилитель– Gain с регулируемым коэффициентом усиления (КУ) и сумматор – Sum, а также интегратор– Integretor (в версии 6.1 и выше данный блок находится в разделе Continuous). Все блоки последовательно перетаскиваем в рабочее окно и закрываем окно Linear (Math).

5. В разделе Connections (Связи) или Signals & Systems (для версии 6.1 и выше) выбираем смеситель– Mux и перетаскиваем в рабочее окно.

6. В рабочем окне приступаем к соединению блоков. Схема модели должна иметь вид:

 

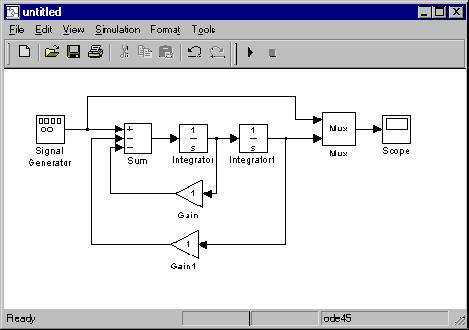Рисунок 1.4 - Схема модели лабораторной работы

 

Копирование блока осуществляется путем перетаскивания с нажатой клавишей Ctrl. Поворот блока осуществляется путем выделения блока и нажатием комбинации клавиш Сtrl+F.

7. Перейдем к настройке системы. Открытие окна настройки блока осуществляется путем двойного щелчка. В блоке Signal Generator рассмотрим доступные нам сигналы. Выбираем Squre – частоту в Гц – 0.02. Смотрим, как система отреагирует на скачкообразное возмущение. Система не является колебательной.

8. Уменьшим КУ по внутреннему контуру (Gain). КУ_Gain = 0.1, т.е. уменьшим демпфирующую силу в 10 раз. Моделируем. Имеем колебательную систему. Теперь нужно поменять собственную частоту, которую определяет нижний КУ_Gain1. Увеличим его в 10 раз. Видим, что увеличилась частота и уменьшилась амплитуда колебаний.

9. В Signal Generator увеличим амплитуду в 5 раз. На внутреннем Gain вместо 0.1 сделаем 0.3 – увеличим коэффициент демпфирования.

Мы убедились, что частота колебаний регулируется усилителем на внешнем контуре, а затухание колебаний регулируется на внутреннем контуре.

10. Ознакомиться с демонстрационными примерами Tracking a bouncing boll, Simple pendulum simulation, Toilet bowl flushing animation и описать один из них по указанию преподавателя:

- назначение системы;

- состав модели;

- особенности движения системы.

ЛАБОРАТОРНАЯ РАБОТА №2

 

МОДЕЛИРОВАНИЕ КОЛЕБАТЕЛЬНЫХ СИСТЕМ

Цель работы:

 

1. Составить математические модели колебательных систем с одной степенью свободы и блок-схемы их набора в пакете Simulink для различных законов демпфирования.

2. Исследовать характер собственных и вынужденных колебаний систем под действием различных внешних сил и ненулевых начальных условий.

 

Теоретическая часть

Простейшая колебательная система (например, грузик на пружине, LC ‑ колебательный контур) имеет одну степень свободы и описывается обыкновенным дифференциальным уравнением первого порядка. Так простейшая одномассовая поступательная система описывается уравнением равновесия сил, действующих на подвижную массу m:

, (2.1)

где 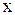- перемещение массы;

- сила инерции;

- демпфирующая сила сопротивления движению, зависящая от скорости ;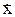

- усилие пружины (восстанавливающая сила);

- внешняя сила.

В зависимости от характера демпфирующей силы уравнение (2.1) движения принимает следующие формы:

1. В случае вязкого трения, характерного для механических крутильных систем, демпфирующая сила является линейной функцией скорости:

, (2.2)

где - линейная сила вязкого трения.

2. В случае квадратичного закона трения, характерного для гидравлических систем, демпфирующая сила является квадратичной функцией скорости:

, (2.3)

где 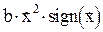- квадратичная демпфирующая сила.

 

а б в

 

Рисунок 2.1. Колебательная система:

а. с вязким линейным трением,

б. с вязким квадратичным трением,

в. с сухим трением.

3. В случае сухого трения, характерного для механических поступательных систем, демпфирующая сила является функцией знака скорости, а величина ее постоянна:

, (2.4)

где - сила сухого трения.

На рис. 2.1 приведены примеры колебательных систем с вязким линейным, вязким квадратичным и сухим трением.

Свободные колебания системы возникают под действием ненулевых начальных условий (, ), либо при скачкообразном приложении силы F(t). Свободные колебания затухают под действием демпфирующей силы, а характер затухания зависит от вида демпфирования (трения).

 

Порядок составления структурной модели

 

Используя уравнения (2.2), (2.3), (2.4) построить блок-схему колебательной системы с различными демпфирующими силами. Для этого необходимо:

1. Разрешить дифференциальное уравнение относительно слагаемого со старшей производной.

2. С помощью цепочки сумматоров собрать модель правой части уравнения.

3. Используя цепочки из двух последовательно включенных интеграторов, получить переменные 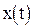и .

4. С помощью усилителей с регулируемым коэффициентом передачи или соответствующих нелинейных блоков получить слагаемые правой части уравнения по п. 1 и подключить их к цепочке сумматоров.

 

Таблица 2.1

№ вар	m	b	c		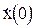	№ вар	m	b	c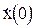
		0.5						0.48
		1.2	0.8					1.32	1.98
		1.2
		1.25	0.25					2.7	1.2
		1.08						0.7
		2.8	0.4					1.6	0.2
		1.35						1.8	1.44
		0.28						0.8
		1.4							4.5
		1.8						2.5
		0.6	0.9					1.6	0.32
		1.75						1.12

5. Проверить блок-схему - в каждом замкнутом контуре число перемен знака должно быть нечетным.

6. Внешнюю силу F(t) моделировать соответствующим генератором.

7. В полученной схеме установить коэффициенты в соответствии с вариантом (табл. 2.1).

8. Набрать модель в рабочем окне SIMULINK.

 

Порядок выполнения работы

 

1. Составить и набрать структурную модель колебательной системы с вязким трением (по уравнению (2.2)). Задать:

· возмущение - единичный скачок;

· начальные условия - нулевые;

· метод моделирования - Рунге-Кутта;

· точность - 0.01;

· длительность моделирования T_k = 50 с.

2. Запустить моделирование командой “Start” или “Счет” (функциональная клавиша F3), по окончании вычисления вывести на экран график процесса x(t) командой “Грф” (F6) и зарисовать.

3. Изменяя коэффициент демпфирования (уменьшая в 2, 4, 10 раз), получить графики соответствующих переходных процессов и зарисовать. Сделать вывод о влиянии коэффициента демпфирования на затухание колебаний.

4. Для заданного коэффициента демпфирования исследовать влияние коэффициента передачи во внешнем контуре на частоту собственных колебаний системы. Для этого увеличивать и уменьшать указанный коэффициент в 2 и 4 раза. Сделать выводы.

5. Исследовать влияние ненулевых начальных условий на движение системы. Для этого установить исходные значения коэффициентов, а сигнал на выходе генератора установить равным 0. Задать последовательно начальные условия 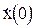и . Зарисовать графики переходных процессов при ненулевых начальных условиях. Сделать выводы.

6. Исследовать поведение системы с вязким трением при подключении в виде возмущающего воздействия синусоидального сигнала при нулевых начальных условиях в районе резонанса. Для этого необходимо найти резонансную частоту системы .

(2.5)

Определить амплитуду установившихся колебаний при частоте возмущающего сигнала 0.5· , , 2· . Сделать выводы.

7. Исследовать систему с вязким трением при подключении в виде возмущающего воздействия меандра (прямоугольных периодических колебаний) при нулевых начальных условиях. Зарисовать процесс x(t) при частоте возмущающего сигнала 0.25· , , 4· . Описать характер движений системы. Сделать выводы.

8. Исследовать колебательные системы с вязким линейным, с вязким квадратичным и с сухим трением (уравнения (2.2), (2.3), (2.4) соответственно) с нулевыми начальными условиями при единичном возмущающем воздействии. Зарисовать полученные выходные характеристики и сделать вывод о влиянии различных демпфирующих сил на вид переходной характеристики.

 

Контрольные вопросы

1. По каким законам уменьшается амплитуда колебаний при вязком линейном трении, при вязком квадратичном трении и при сухом трении?

2. Как изменяется амплитуда вынужденных колебаний в зависимости от частоты возмущающей силы?

3. Сколько собственных частот имеют колебательные системы, описываемые обыкновенными уравнениями 3-го, 4-го, 5-го, 6-го порядка?

4. Как изменяется затухание колебаний при изменении коэффициента демпфирования?

5. Как изменится собственная частота колебательной системы при изменении массы?

Литература

 

1. Пановко Я.Г. Введение в теорию колебаний. - М.: Наука, 1991.

2. Тимошенко С.П. Колебания в инженерном деле. - М.: Физматгиз, 1959.

 

 

ЛАБОРАТОРНАЯ РАБОТА №3

123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: