Генерация случайных процессов с заданной спектральной плотностью

 

Цель работы:

Моделирование случайного процесса с заданной спектральной плотностью, путем применения линейного формирующего фильтра.

Разработана с магистром Икол Е.Ю.

 

Основные определения

Случайный сигнал – сигнал, мгновенное значение которого заранее не известно и может быть предсказано лишь с некоторой вероятностью, меньшей единицы.

Случайный процесс (СП) – математическая модель изменяющегося во времени случайного сигнала.

Случайный процесс X(t) – функция, значения которой в любой момент времени t, являются случайными величинами.

СП X(t) стационарен в широком смысле, если его математическое ожидание M_x и дисперсия D_x не зависят от времени, а корреляционная функция R_x зависит не от самих моментов времени, а только от интервала между ними ф = t₁ – t₂:

 

R_x(t₁,t₂) = R_x(t₂ – t₁) = R_x(ф),

M_x(t) = const, D_x(t) = const.

 

Спетральная плотность – величина, которая пропорциональна средней мощности процесса в интервале частот от щ до щ + dщ.

Белый шум – стационарный СП, спектральная плотность мощности которого постоянна на всех частотах: W(щ) = W₀ = const.

Теоретическая часть

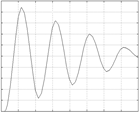
Задачей данной работы является генерация случайного процесса (помехи), представляющий собой белый шум, содержащий периодическую (неслучайную) помеху с частотой щ₁.

Для чего нужны модели таких сигналов?

Многие сигналы являются детерминированными, то есть их временная зависимость y(t) известна и не меняется при неоднократном моделировании. Такие сигналы удобны для аналитического описания и анализа систем. Но на практике большинство реальных сигналов не являются детерминированными. Одной из причин этого является засоренность сигналов шумами и помехами, имеющими случайный характер с тем или иным спектром. Таким образом, для получения реального сигнала, используемого на практике, необходимо уметь генерировать помехи и прежде всего белый шум.

Предположим, что в нашем распоряжении имеется генератор шума, выходной сигнал которого имеет спектральную плотность S_x(щ). Для имитации шумов имеющих место в реальной системе, требуется воспроизвести случайный сигнал со спектральной плотностью S_y(щ). Для этого необходимо определить передаточную функцию Ф(jщ) линейного формирующего фильтра.

 

X(t) Y(t)

S_x(щ) S_y(щ)

 

Рис. 7.1. Линейная система

 

Докажем это. Из теории автоматического управления известно, что спектральная плотность сигнала на выходе линейной системы равна квадрату модуля частотной функции, умноженного на спектральную плотность входного сигнала:

.

 

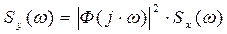На основании этого можно найти:

.

Если в качестве входного сигнала используется белый шум, для которого S_x(щ) = 1, то

|Ф(jщ)|² = S_y(щ).

 

То есть спектральная плотность сигнала на выходе в этом случае зависит только от параметров линейного фильтра.

В данной работе на вход фильтра кроме белого шума необходимо также подавать периодический сигнал (синусоиду), так как в реальных системах кроме помех, имеющих случайный характер, могут присутствовать помехи неслучайного характера.

Как правило, в качестве линейного формирующего фильтра используется колебательное звено:

 

, (7.1)

где ,

щ ₀ – резонансная частота.

При создании активных узкополосных фильтров с передаточной функцией вида (7.1) применяют избирательные усилители, которые из поступающей на вход совокупности сигналов широкого диапазона частот выделяют группу сигналов близких частот, несущих полезную информацию.

Порядок выполнения работы

1. В пакете Simulink составить и набрать структурную модель, позволяющую генерировать случайный процесс (белый шум), содержащий периодическую составляющую с частотой щ₁. Данная модель должна представлять собой фильтр (колебательное звено с передаточной функцией (1)), на вход которого подается суммарный сигнал белого шума и синусоиды f(t)=A·sin(щ₁·t).

2. Изменяя коэффициент демпфирования о (в интервале 0.3 ÷ 0.7 методом деления пополам^*) в передаточной функции фильтра получить на его выходе случайный сигнал с заданной спектральной плотностью.

При составлении модели необходимы будут блоки:

­ Band Limited White Nose – генератор белого шума;

­ Блок Averaging Power Spectral Density из библиотеки Simulink Extras – предназначен для наглядного представления формы выходного сигнала и его энергетического спектра; необходимо использовать следующие настройки данных блоков (рис. 7.2):

 

Рисунок 7.2

^* Метод основан на делении текущего отрезка [a, b] на две равные части с последующим выбором одной из половин, в которой находится максимум в качестве следующего текущего отрезка. Чем ближе коэффициент демпфирования о к 0.3, тем более выражена резонансная частота в спектральной плотности выходного сигнала и наоборот.

 

 

Таблица 7.1

№	A	щ1	щ0	Stop time	Sy(щ)
	0.1				рис. 7.3.1
	0.1		12.5		рис. 7.3.2
	0.1		4.5		рис. 7.3.3
	0.1	4.5	6.7		рис. 7.3.4
	0.1				рис. 7.3.5
	0.1				рис. 7.3.6
	0.1		11.1		рис. 7.3.7
	0.1		3.84		рис. 7.3.8
	0.1		7.69		рис. 7.3.9
	0.01				рис. 7.3.10
	0.04				рис. 7.3.11
	0.01	2.5			рис. 7.3.12

 

Где Stop time – время моделирования (Simulation → Simulation parameters → Stop time).

 

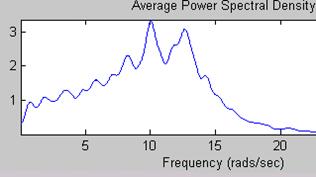
1) 2)

 

3) 4)

5) 6)

7) 8)

9) 10)

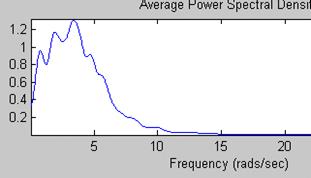
11) 12)

Рисунок 7.3

 

 

Литература

 

1. Жовинский В.Н. Генерирование шумов для исследования автоматических систем. М., “Энергия”, 1968.

2. Дьяконов В. SIMULINK 4. Специальный справочник. – СПб: Питер, 2002.

 

ЛАБОРАТОРНАЯ РАБОТА № 8

ИДЕНТИФИКАЦИЯ ДИНАМИЧЕСКИХ ОБЪЕКТОВ

ПО ПЕРЕХОДНЫМ ФУНКЦИЯМ

 

Теоретические сведения

Идентификация (identificare, лат. - узнавать) – оценивание структуры и параметров системы по результатам экспериментов с ней. Наиболее информативна идентификация системы по результатам активных экспериментов (с вмешательством в работу объекта с помощью пробных сигналов). Наиболее удобный пробный сигнал – скачкообразное изменение управляющего сигнала или возмущения, действующего на систему.

Металлургические машины и агрегаты, как правило, работают в непрерывно-дискретном режиме, поэтому вместо подачи пробных сигналов часто можно использовать скачкообразные технологические возмущения (напр., загрузка очередной порции шихты в доменную печь, начало продувки в конверторе, захват заготовки прокатными валками и др.).

Разработана с ас. Тригуб И.Г.

Зарегистрированный график изменения выходной величины при скачкообразном возмущении на входе – переходную функциютехнологического объекта управления (ТОУ) можно использовать для его идентификации.

Если поставлена задача автоматизации ТОУ, то идентификацию следует проводить средствами теории автоматического управления (ТАУ), т.е. представить объект в виде некоторого соединения типовых звеньев ТАУ, линейных и нелинейных.

Получив график переходной функции, вначале выполняют структурную идентификацию – оценивание порядка передаточной функции объекта, вида его нелинейностей. При этом основываются на особенностях графиков переходных функций (таб.).

 

Таблица 8.1

График переходной функции	Особенности	Соответствующее типовое звено
		Название	Передаточная функция
Линейные объекты
	Монотонно возрастающая функция. Скорость роста монотонно убывает.	Инерционное
	Наличие затухающих колебаний. Огибающая колебаний описывается экспонентой.	Колебательное

 

 

Точка перегиба	Наличие точки перегиба на кривой. В начале скорость роста возрастает, затем убывает.	Апериодическое звено 2-го порядка
Точка перегиба	Наличие затухающих колебаний, а также точки перегиба на кривой разгона.	Объект 3-го порядка = последователь-ное соединение инерционного и колебательного звеньев.
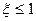
	Затухающие колебания наложены на монотонно возрастающую функцию.
	Наличие незатухающих колебаний, наложенных на кривую разгона. Как правило, это гармоническая помеха.	Консервативное звено, параллельное объекту.
Нелинейные объекты
t	Наличие “чистого запаздывания”	Звено запаздывания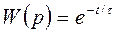
	Наличие “люфта”

 

	Наличие ограничения
	Огибающая затухающих колебаний – прямая линия	Звено “сухое трение”
	Огибающая затухающих колебаний – гипербола (в начале колебания затухают быстро, затем скорость затухания резко убывает)	Квадратичный закон демпфирования

 

Далее выполняют параметрическую идентификацию – оценивание параметров системы (коэффициентов передаточной функции либо уравнений нелинейных звеньев) приближенными численными методами ТАУ.

Например, из курса ТАУ известно, что графически можно определить постоянную времени инерционного звена (как это показано в таблице) или постоянную времени колебательного звена:

 

Т = Т_к / 2p,

 

где Т_к – период собственных колебаний,

а коэффициент демпфирования колебаний определяют по графику в зависимости от величины относительного перерегулирования

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: