Оценивание случайных параметров и регрессия

Изучить средства статистической обработки экспериментальных данных и возможности регрессионного анализа в среде MATLAB (в графическом окне).

Теоретическая часть

В MATLAB 6 в пункте меню Tools графического окна содержатся программные средства для быстрой обработки экспериментальных данных. По команде Tools / Data statistics открывается окно с рядом статистических параметров для оценки выборки случайных величин:

­ min – минимальное,

­ max – максимальное,

­ mean – среднее арифметическое значение,

­ median – медиана,

­ std – среднеквадратическое отклонение.

Покоманде Basic Fitting открывается окно, дающее доступ к ряду видов аппроксимации и регрессии: сплайновой и полиномиальной со степенями от 1 (линейная аппроксимация) до 10, в том числе со степенью 2 (квадратичная аппроксимация) и 3 (кубическая аппроксимация).

Полиномиальная регрессия. Вид уравнения регрессии выбирается из особенностей изучаемой системы случайных величин. Существуют следующие виды полиномиальной регрессии:

­ одномерная линейная регрессия, зависимость от имеет вид:

,

где 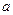- коэффициент при , а - постоянная. Коэффициент 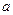имеет тот же знак, что и коэффициент корреляции (характеризует меру линейной зависимости между величинами и ).

­ одномерная нелинейная регрессия:

,

где 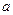- постоянная, - коэффициент при , - коэффициент при и т.д. Например: - квадратичная аппроксимация ;

- кубическая аппроксимация .

Для выполнения полиномиальной регрессии (аппроксимации) надо отметить флажком необходимый вид в окне регрессии (Basic Fitting). Установка флажка Show equations выводит в графическом окне записи уравнений регрессии.

Сплайновая интерполяция. Практически нельзя назвать этот подход полноценной аппроксимацией, так как в данном случае нет единого выражения для аппроксимирующей функции. Для выполнения данного вида интерполяции необходимо отметит флажком spline interpolant в окне регрессии. На каждом интервале приближения используется кубический полином с новыми коэффициентами, поэтому вывод аппроксимирующей функции не предусмотрен. Сплайновая интерполяция лучше, когда нужно эффективное сглаживание быстро меняющихся от точки к точке данных и когда исходная зависимость может быть графически изображена с помощью гибкой линейки.

Оценка погрешности аппроксимации. Средства обработки данных графического окна позволяют строить столбчатый (Bar plot) или линейчатый (Line plot) графики погрешностей в узловых точках и наносить на эти графики норму погрешности (среднеквадратическое отклонение данных 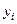от аппроксимирующей функции в точках ):

,

где - количество данных.

Для вывода графика погрешности необходимо в окне регрессии (Basic Fitting) установить флажок Plot residuals и в меню под этим флажком выбрать тип графика. Для нанесения нормы погрешности на график надо установить флажок Show norm of residuals. В меню над данным флажком можно выбрать Separate figure – построение графика погрешности в отдельном окнеили Subplot – построение графика погрешности под графиком узловых точек и функций аппроксимации.

Порядок выполнения работы:

1. В командном окне MATLAB задать некую зависимость векторами координат ее точек. Например:

>> ;

>> ;

Построить точечный график функции используя команду:

>> ;

2. Используя возможности графического окна выполнить аппроксимацию данных с помощью полиномов разных степеней (от 1 до 7), вывести записи уравнений регрессии, оценить погрешность аппроксимации, определить норму погрешности. Сделать вывод.

3. В командном окне MATLAB создать данные – функциональную зависимость ,

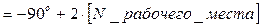где (начальная фаза) ; рад/с; ; ; интервал дискретизации .

Для этого необходимо сперва сформировать вектор :

>>

а затем задать указанную функциональную зависимость:

>> ;

Построить график функции :

>> ;

4. “Зашумить” данные помехой с нормальным распределением использую функцию :

>> - генерация помехи,

где , , - число столбцов, - число строк.

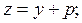>> - зашумляем данные (здесь и вектора, для того, что бы их сложить они должны быть одинаковой длины, поэтому при задании помехи необходимо задать =1, а =40 (что соответствует длине вектора , изменяющегося от 1 до 40, а следовательно и длине вектора ).

Построить точечный график “зашумленных” данных:

>> ;

5. Для полученных “зашумленных” данных выполнить действия, описанные в пункте 2, а также определить максимальное, минимальное, среднее значение и среднеквадратическое отклонение.

6. Выполнить сплайновую интерполяцию используя возможности графического окна и сравнить полученные результаты с полиномиальной регрессией. Сделать выводы.

Литература

1. Гмурман В.С. Теория вероятностей и математическая статистика. Учебное пособие. М.: Высшая школа, 1972.

2. Дьяконов В. SIMULINK 4. Специальный справочник. – СПб: Питер, 2002.