 |
Моделирование нелинейных и дискретных систем
|
|
|
|
Цель работы:
Реализация математических моделей систем в пакете структурного моделирования Simulink.
Порядок составления структурной модели в Simulink для системы, описываемой дифференциальным уравнением
1. Разрешить дифференциальное уравнение относительно старшей производной.
2. С помощью сумматора Sum собрать модель правой части уравнения.
3. Используя цепочки из последовательно включенных интеграторов Int (количество которых определяется порядком уравнения), получить неизвестную функцию и ее производные.
4. С помощью усилителей Gain с регулируемым коэффициентом передачи или соответствующих нелинейных блоков получить слагаемые правой части уравнения (полученного в п.1) и подключить их к сумматору Sum.
5. Внешнюю силу F(t) моделировать соответствующим генератором.
6. В полученной схеме установить коэффициенты в соответствии с заданным вариантом.
7. Проверить модель на структурную устойчивость: число перемен знака сигнала в каждом замкнутом контуре должно быть нечетным.
8. Набрать модель в рабочем окне Simulink.
9. Добавить в модель необходимые приемники сигналов Scope, Display, X-Y plot.
Уравнение Ван дер Поля
Классическое нелинейное дифференциальное уравнение Ван дер Поля обычно записывается в форме:
. (1)
Это уравнение описывает колебательную систему с переменным коэффициентом демпфирования. Если перемещения малы, то коэффициент при 
отрицателен, что соответствует отрицательному демпфированию и, следовательно, развитию автоколебаний. При больших перемещениях демпфирование становится положительным, то есть устойчивые автоколебания могут существовать только при отсутствии демпфирования. Уравнение достаточно хорошо описывает работу некоторых генераторов колебаний. Качественный характер решения зависит от значения параметра 
. При малых сравнительно с единицей значениях получаются решения одного вида, тогда как при больших значениях решения имеют другой вид.
|
|
|
Задание: промоделировать уравнение (1) при значениях 
, 
, 
.
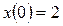Уравнение Рэлея
Уравнение Рэлея эквивалентно уравнению Ван дер Поля (1),
(2)
но проще, так как нелинейное слагаемое содержит лишь производную 
, а не две переменные 
и 
.
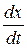Задание: промоделировать уравнение (2) при значениях 
, 
, 
.
Уравнение Матье
. (3)
Уравнение Матье представляет собой уравнение второго порядка с периодическим коэффициентом, где 
и 
- постоянные.
Задание: промоделировать уравнение (3) при значениях 
, 
, , 
.
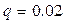Линейные уравнения второго порядка с переменными коэффициентами
Уравнение Лежандра:
. (4)
Задание: промоделировать уравнение (4) при значениях 
, 
, 
.
Модель нелинейной электрической цепи
. (5)
Данное уравнение приближенно описывает цепь, содержащую индуктивность с насыщающимся стальным сердечником – нелинейный элемент. Слагаемое, содержащее 
, - нелинейный член уравнения.
Задание: промоделировать уравнение (5) при значениях 
, 
, 
, 
, 
, 
.
Резонансный контур с переменной емкостью
. (6)
Используя данное уравнение, определяют мгновенное значение заряда конденсатора 
входящего в состав электрического контура с постоянной индуктивностью 
и переменной емкостью, мгновенное значение которой определяется как 
.
-среднее значение; 
- относительное изменение (
); 
- круговая частота изменений емкости ( << 
); 
.
Задание: промоделировать уравнение (6) при значениях 
, 
, 
, 
, 
.
Модель нелинейной системы
. (7)
С помощью данного уравнения описывают движение постоянной массы, прикрепленной к нелинейной пружине, жесткость которой растёт по мере возрастания деформации.
|
|
|
Задание: промоделировать уравнение (7) при значениях 
, 
.
Уравнения Вольтерра
Данные уравнения описывают борьбу между двумя видами животных:
. (8)
В этих уравнениях 
и 
- численности двух видов, живущих на какой-либо определённой территории. Эти виды находятся в конкурентной борьбе друг с другом, хотя бы потому, что они потребляют один и тот же корм. 
, 
, 
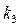и 
- положительные действительные параметры, причём > 
. Первый член правой части соответствует нормальному увеличению численности, которое имело бы место в отсутствии ограничивающих факторов. Второй член выражает уменьшение численности, которое возникает в результате конкурентной борьбы двух видов животных.
Задание: промоделировать систему (8) при значениях 
, 
, 
, 
, 
, 
.
|
|
|
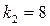