 |
Задачи для самостоятельного решения
|
|
|
|
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Методические указания к выполнению
Рассчетно-графического задания
По физике №2
Иваново 2008
Составители: В.Х. Костюк,
О.А. Кабанов,
Г.А. Шмелева
Редактор В.К. Ли-Орлов
Содержат математические формулировки основных определений и законов молекулярной физики и термодинамики с пояснениями, примеры решений типовых задач, образцы оформления решений, задания для самостоятельной работы студентов по курсу "Молекулярная физика и термодинамика". Предназначены для обеспечения самостоятельной работы студентов.
Утверждены цикловой методической комиссией инженерно-физического факультета.
Рецензент
кафедра физики ГОУВПО "Ивановский государственный энергетический университет имени В.И. Ленина"
Молекулярная физика и термодинамика
Методические указания к выполнению расчетно-графического задания по физике №2
Составители: КОСТЮК Владимир Харитонович,
КАБАНОВ Олег Альбертович,
ШМЕЛЕВА Галина Александровна
Редактор М.А. Иванова
Лицензия ИД № 05285 от 4 июля 2001 года
Подписано в печать Формат 60х84 
.
Печать плоская. Усл. печ. л. 2,79. Тираж 150 экз. Заказ №
ГОУВПО "Ивановский государственный энергетический университет имени В.И. Ленина"
Отпечатано в РИО ИГЭУ
153003, г. Иваново, ул. Рабфаковская, 34.
Программа курса
"Молекулярная физика и термодинамика"
Термодинамические системы. Методы молекулярной физики, статистической физики и термодинамики. Термодинамические параметры. Состояния термодинамической системы. Уравнения состояния идеального газа. Термодинамические процессы. Диаграммы состояний и процессов.
|
|
|
Основное уравнение молекулярно-кинетической теории идеального газа. Средняя кинетическая энергия молекул. Абсолютная температура. Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы молекул. Распределение молекул идеального газа по скоростям – распределение Максвелла. Барометрическая формула. Распределение молекул идеального газа по энергиям в потенциальном поле – распределение Больцмана.
Термодинамика идеального газа. Термодинамические функции: внутренняя энергия, работа, количество теплоты. Первый закон термодинамики. Работа в изохорном, изобарном и изотермическом процессах. Теплоемкость. Теплоемкость идеального газа. Соотношение Майера. Адиабатный процесс. Уравнение Пуассона.
Циклические процессы. Цикл Карно. Тепловая машина. КПД тепловой машины. КПД идеальной тепловой машины. Теорема Карно.
Обратимые и необратимые процессы. Второй закон термодинамики. Энтропия. Теорема Нернста. Энтропия идеального газа. Понятия порядка и беспорядка. Статистический вес. Формула Больцмана. Статистический смысл второго закона термодинамики.
Кинетические явления. Среднее число столкновений и средняя длина свободного пробега молекул. Диффузия, теплопроводность и внутреннее трение.
Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы реального газа. Фазовые переходы 1-го рода. Критическое состояние вещества.
I. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
ПРОЦЕССЫ ИДЕАЛЬНОГО ГАЗА
1. Уравнения состояния идеального газа (производные формы):
,
,
,
,
,
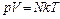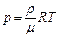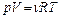где р – давление;
n – концентрация молекул;
k = 1,38 10-23 Дж/К; – постоянная Больцмана;
T – абсолютная температура;
V – объём;
N – число молекул;
ρ – плотность газа;
μ – молярная масса;
m – масса газа;
ν – число молей;
R = 8,31 Дж/(моль·К) – универсальная газовая постоянная.
2. Закон Дальтона:
|
|
|
,
где p – давление смеси газов, pi – парциальное давление i – го компонента смеси газов.
3. Термодинамические процессы в идеальном газе постоянной массы:
а) изотермический, Т = const,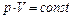 
;
б) изобарный, p= const, 
;
в) изохорный, V = const, 
.
Примеры решения задач
Задача 1. В баллоне объёмом 20 л находится аргон под давлением 1,0 МПа и температуре 300 К. После того как из баллона было взято 20,0 г аргона, температура в баллоне понизилась до 280 К. Определить давление газа, оставшегося в баллоне.
Дано: Решение:
V = 20 л = 2,0·10-2 м3 Для решения задачи воспользуемся
р1 = 1,0 МПа = 1,0·106 Па уравнением состояния идеального
Т1 = 300 К газа, применив его к начальному и
Т2 = 280 К конечному состояниям газа:
Δm = 20,0 г = 2,0·10-2 кг 
, (1)
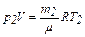р2 –? 
. (2)
Из уравнений (1) и (2) выразим m1 и m2 и найдём их разность:
,
откуда находим
. (3)
Проверку решения проведем по размерности физических величин. В правую часть вместо символов величин подставим их единицы измерения. В правой части два слагаемых. Первое из них имеет размерность давления, так как состоит из двух множителей, первый из которых – давление, а второй – безразмерный. Проверим второе слагаемое:
.
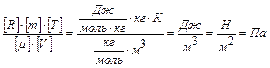Вычисления произведём по формуле (3) с учётом, что для аргона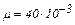 
кг/моль.
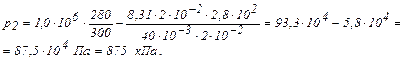Ответ: 875 кПа.
Задача 2. В сосуде находится смесь 14,0 г азота и 16,0 г кислорода при температуре 300 К и давлении 8,3 кПа. Определить плотность этой смеси, считая газы идеальными.
Дано: Решение:
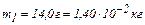Для каждого компонента в смеси
газов можно записать уравнения
состояния:
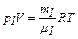, (1)
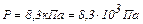
. (2)
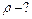
Давление смеси равно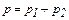 
(по закону Дальтона). Суммируя (1) и (2), с учётом закона Дальтона найдём объём газа
.
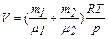Для плотности смеси находим
.
Проверка размерности:
.
Вычисления:
.
Ответ: 0,1 кг/м3.
Задача 3. Поршневым воздушным насосом откачивают баллон объёмом 10,0 л. За один цикл (ход поршня) насос захватывает объём 0,4 л. Через сколько циклов давление в баллоне уменьшится от 0,1 МПа до 0,1 кПа? Процесс считать изотермическим, газ – идеальным.
Дано: Решение:
V = 10 л = 1,0 10-2 м3 Для изотермического процесса в первом
ΔV = 0,4 л = 0,4 10-3 м3 и следующих циклах можно записать
р0 = 0,1 МПа = 1,0 105 Па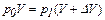 
,
рN = 0,1 кПа = 100 Па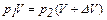 
,
Т = const -----------------------
N –?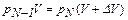 
.
Получаем рекуррентную формулу
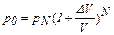, (1)
где N – число циклов. Прологарифмировав соотношение (1), получим для числа циклов
|
|
|
. (2)
Правая часть (2) содержит отношения однородных величин и является безмерной.
Вычисления:
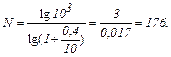
Ответ: 176 циклов.
Задача 4. Идеальный газ совершает процесс, в котором давление изменяется в зависимости от объёма по закону p=p0–αV2, где p0=0,1 МПа, α=1,0·107 Па·моль2/м6. Количество вещества газа равно 1 моль. Определить максимальную температуру газа в процессе.
Дано: Решение:
р = р0 – αV2 Найдём зависимость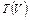 
. Для этого
р0= 0,1 МПа = 105 Па воспользуемся уравнением состояния для
α = 1,0·107 Па·моль2/м6 одного моля газа
Тmax –? 
.
Исключая давление, получим
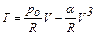. (1)
Из условий
находим максимум функции T(V). Получается, что в области положительных значений V и Т зависимость (1) при объёме моля газа
имеет максимальную температуру, равную
.
Проверка размерности:
.
Вычисления:
.
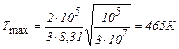Ответ: 465 К.
Задачи для самостоятельного решения
1.1. Определить число молекул водорода в объёме 1,55 л при температуре 27 °С и давлении 750 мм рт. ст.
1.2. Определить концентрацию и плотность азота при температуре 15 °С и давлении 10-4 мм рт. ст.
1.3. Определить массу одной молекулы: азота (N2), аммиака (NH3), ацетилена (C2H2),ацетона (CH3COCH3).
1.4. Сколько молекул содержится в 22 г водорода?
1.5. Сколько молекул газа находится в колбе объёмом 2 л при давлении 0,66·105 Па и температуре 17 °С.
1.6. Плотность некоторого газа при нормальных физических условиях (р = 760 мм рт. ст., t = 0 °С) составляет 88,15 г/м3. Определить молярную массу газа.
1.7. Масса кислорода 0,02 кг, температура 40 °С. Какое давление оказывает кислород на стенки сосуда объемом 200 л?
1.8. Давление кислорода 2·105 Па, плотность 1,2 кг/м3. Определить температуру.
1.9. Определить массу метана (СН4), который содержится в баллоне объемом 15 л при давлении 106 Па и температуре 27 °С.
1.10. Определить давление, оказываемое 1 кг азота на стенки сосуда объемом 1 м3, при температуре 27 °С.
1.11. Баллон ёмкостью 12 л наполнен азотом при давлении 8,1·106 Па и температуре 17 °С. Какое количество азота находится в баллоне?
1.12. На сколько уменьшится масса воздуха в комнате объемом 50 м3 при повышении температуры в ней от 17 °С до 27 °С? Атмосферное давление остается постоянным и равным 760 мм рт. ст.
|
|
|
1.13. 716 мг органического соединения с формулой (С3Н6О)n превращается при 200 °С и давлении 750 мм рт. ст. в пар объемом 242,6 см3. Определить число n.
1.14. Определить химическую формулу молекулы некоторого соединения углерода с кислородом, если 1 г этого вещества в газообразном состоянии создаёт в сосуде объёмом 1 л давление 0,56·105 Па при температуре 27 °С.
1.15. Сколько электронов содержится в кислороде, который занимает при давлении 106 Па и температуре 200 °С объём 1 л?
1.16. В баллоне объемом 15 л находится 96 г неизвестного газа при давлении 106 Па и температуре 300 К. Определить химическую формулу газа, если в состав молекулы газа входят атомы водорода и углерода.
1.17. Определить плотность паров ртути при 420 °С и давлении 2,3 мм рт. ст. Молярная масса ртути 200 г/моль.
1.18. Определить подъёмную силу заполненного гелием аэростата, представляющего собой шар радиусом 6 м. Давление гелия и окружающего воздуха равно 760 мм рт. ст., температура 17 °С.
1.19. На сколько градусов надо нагреть воздух внутри воздушного шара, чтобы шар взлетел? Диаметр шара 10 м, масса его оболочки 10 кг. Атмосферное давление 760 мм рт. ст., температура окружающего воздуха 27 °С.
1.20. В баллоне находится полый стальной шарик радиусом 2 см и массой 5 г. Какое давление воздуха надо создать в баллоне, чтобы шарик находился в состоянии невесомости? Температура воздуха 20 °С. Считать, что для воздуха справедливо уравнение состояния идеального газа.
1.21. В сосуд, на дне которого лежит твёрдый шар радиусом 5 см, нагнетают воздух при температуре 27 °С. Когда давление в сосуде становится равным 2·105 Па, шар поднимается. Определить массу шара.
1.22. При изобарном нагревании газа на 1 °С его объём увеличился на 1/335 часть начального объема. Определить начальную температуру газа.
1.23. До какой температуры нужно нагреть баллон объемом 1 л, содержащий 17,5 г водяного пара, чтобы баллон разорвался? Стенки баллона выдерживают давление не более 107 Па.
1.24. Цилиндрическая трубка длиной 66 см наполовину погружена в ртуть. Верхний конец трубки закрывают пальцем и вынимают трубку из ртути. Часть ртути при этом вытекает. Какой длины столбик ртути остался в трубке? Атмосферное давление равно 750 мм рт. ст.
1.25. Определить плотность смеси 4 г водорода и 32 г кислорода при температуре 7 °С и давлении 700 мм рт. ст.
1.26. Узкая цилиндрическая трубка, закрытая с одного конца, содержит воздух, отделённый от наружного воздуха столбиком ртути длиной 15 см. При вертикальном положении трубки, когда закрытый конец находится вверху, длина столбика воздуха равна 30 см, когда закрытый конец находится внизу, длина столбика воздуха равна 20 см. Определить атмосферное давление.
|
|
|
1.27. Горизонтально расположенный цилиндр разделён подвижным поршнем на две части. В одной части находится 8 г кислорода, а в другой – некоторое количество гелия. Определить массу гелия, если он занимает 0,67 часть объёма всего цилиндра. Температура газов одинакова.
1.28. Горизонтально расположенный цилиндр разделён подвижным поршнем на две части. В одной части находится 3 г кислорода, а в другой – 17 г азота. Какую часть объёма всего цилиндра занимает водород?
1.29. В вертикально расположенном закрытом цилиндрическом сосуде с площадью основания 25 см2 находится газ, разделённый поршнем массой 1 кг на два равных отсека. Масса газа под поршнем в два раза больше массы газа над поршнем. Определить давление газа в каждом отсеке. Трением в системе пренебречь, температура в обеих частях сосуда постоянна.
1.30. При нагревании газа в закрытом сосуде на 1 0С, давление газа увеличилось на 0,2 %. Определить начальную температуру газа.
1.31. В баллоне находился газ при атмосферном давлении 105 Па и температуре 10 °С. При открытом вентиле баллон нагрели, а затем вентиль закрыли и баллон остудили до начальной температуры. Давление газа в баллоне после этого стало равно 0,7 атм. На сколько градусов нагрели баллон?
1.32. Сколько молекул воздуха вышло из комнаты объёмом 120 м3 при увеличении температуры от 15 °С до 25 °С? Атмосферное давление 760 мм рт. ст.
1.33. Из баллона объемом 10 л вследствие неисправности вентиля вытекает водород. Начальная температура газа 7 °С, давление 5·106 Па. Через некоторое время при температуре 17 °С манометр показал такое же давление. На сколько уменьшилась масса газа?
1.34. Определить молярную массу неизвестного газа, свойства которого соответствуют свойствам смеси 64 г кислорода и 8 г гелия.
1.35. Сухой воздух по массе состоит из азота (75,52 %), кислорода (23,15 %), аргона (1,28 %) и углекислого газа (0,05 %). Пренебрегая примесями других газов, определить молярную массу сухого воздуха.
1.36. В сосуде объёмом 2 м3 при температуре 100 °С и давлении 4·105 Па находится смесь кислорода и 8 кг сернистого газа (SO2). Определить парциальные давления газов.
1.37. Плотность смеси азота и водорода равна 0,3 кг/м3 при температуре 320 К и давлении 2·105 Па. Определить концентрацию молекул водорода в смеси.
1.38. В закрытом сосуде емкостью 1 м3 находится 0,9 кг водяного пара и 1,6 кг кислорода. Определить давление этой смеси на стенки сосуда при температуре 600 °С.
1.39. В сосуде находится 14 г азота и 9 г водорода при температуре 20 °С и давлении 105 Па. Определить молярную массу смеси и объём сосуда.
1.40. Определить массу водяных паров в 1 м3 воздуха при давлении 760 мм рт. ст., относительной влажности воздуха 60 % и температуре 25 °С. Давление насыщенного водяного пара при этой температуре равно 3167 Па.
1.41. В баллоне ёмкостью 2 м3 содержится смесь азота и окиси азота (NO). Масса смеси равна 14 кг, температура 300 К, давление 0,6·106 Па. Определить массу окиси азота.
1.42. Плотность смеси азота и водорода равна 0,3 кг/м3. Какова концентрация молекул азота в смеси, если концентрация молекул водорода в смеси равна 4,2·1019 см-3?
1.43. Молярная масса смеси кислорода и гелия равна 18 г/моль. Масса гелия 8 г. Определить массу кислорода в смеси.
1.44. В сосуде объёмом 10 л содержалась смесь 2 г водорода и 2 г кислорода. В результате реакции в баллоне образовалась вода. Определить парциальное давление водорода при 17 °С.
1.45. В сосуде находится смесь азота и водорода. При температуре Т и давлении р азот полностью диссоциирован на атомы, а водород остается двухатомным. При температуре 2Т и давлении 3 Р, оба газа полностью диссоциированы. Определить отношение масс азота и водорода в смеси?
1.46. При комнатной температуре жидкая четырёхокись азота N2O4 частично диссоциирует в двуокись азота NO2, которая превращается в газ. В сосуде объёмом 250 см3 находится 0,9 г N2O4 при температуре 27 °С и давлении 960 мм рт. ст. Определить степень диссоциации газа.
1.47. В результате диссоциации из одной исходной молекулы газа образуются две одинаковые молекулы газа. Определить степень диссоциации газа, если молярная масса образующейся смеси составляет 62,5 % молярной массы исходного газа?
1.48. Определить массу воздуха в колодце площадью сечения 2 м2 и глубиной 6 м. Температура воздуха уменьшается в зависимости от глубины по линейному закону от 27 °С у поверхности до 7 °С на дне. Атмосферное давление 100 кПа.
1.49. Воздух находится под давлением 0,1 МПа между двумя одинаковыми горизонтальными пластинами. Температура возрастает линейно от 17 °С у нижней пластины до 117 °С у верхней. Объём пространства между пластинами 3 л. Определить массу воздуха между пластинами.
1.50. В результате диссоциации из одной исходной молекулы газа образуются две одинаковые молекулы газа. Степень диссоциации газа равна 60 %. Определить молярную массу образующейся смеси.
1.51. Давление воздуха внутри бутылки при температуре 17 °С равно 0,1 МПа. На сколько градусов нужно нагреть бутылку, чтобы пробка вылетела? Без нагревания пробку можно вытянуть, приложив силу 15 Н. Площадь поперечного сечения пробки 3 см2.
1.52. Сколько качаний нужно сделать поршневым насосом с рабочим объёмом 1 л, чтобы повысить давление от 0,1 МПа до 0,3 МПа в сосуде объёмом 10 л?
1.53. За какое число качаний поршневым насосом с рабочим объёмом 1 л можно понизить давление от 0,1 МПа до 50 кПа в сосуде объёмом 10 л?
1.54. Объём идеального газа изменяется пропорционально давлению по закону V=αp, где α > 0. Во сколько раз изменится давление газа при уменьшении температуры от 327 °С до 27 °С?
1.55. Объём идеального газа изменяется пропорционально давлению по закону V=αp, где α > 0. Во сколько раз изменится объём газа при увеличении температуры от 400 К до 625 К?
1.56. В некотором процессе давление газа изменяется по закону p=αV2, где α > 0. Определить начальную температуру газа, если после увеличения объёма в 1,2 раза температура газа оказалась равной 200 °С.
1.57. Давление газа изменяется по закону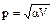 
, где α > 0. Во сколько раз изменится температура газа при увеличении его объёма в 1,4 раза?
1.58. Определить наименьшее давление идеального газа в процессе, в котором температура изменяется по закону T=T0+αV3, где Т0=273 К, α=4·109 К/м3, V – объём моля газа.
1.59. Определить максимальную температуру идеального газа в процессе, в котором давление изменяется по закону р=р0–αV3, где р0=0,1 МПа, α=2·108 Па/м3, V – объём моля газа.
1.60. В левой части цилиндрического сосуда длиной 1 м, разделённого теплонепроницаемым поршнем, находится водород, а в правой – гелий. Объём гелия в 3 раза больше объёма водорода. При нагревании гелия поршень сместился на 5 см. На сколько градусов изменилась температура гелия, если начальные температуры газов были одинаковы? Температура водорода поддерживается постоянной и равной 300 К.
II. ОСНОВЫ
|
|
|
