IV. Второй закон термодинамики

 

1. Коэффициент полезного действия (КПД) тепловой машины

,

где A – работа, совершенная тепловой машиной за цикл;

Q_н – количество теплоты, полученное от нагревателя за цикл;

Q_х – количество теплоты, переданное холодильнику за цикл.

2. КПД идеальной тепловой машины, работающей по циклу Карно

,

где T_х – температура холодильника; T_н – температура нагревателя.

3. Бесконечно малое изменение энтропии термодинамической системы .

Изменение энтропии при переходе системы из состояния 1 в состояние 2: .

4. Энтропия одного моля идеального газа (определяется с точностью до аддитивной постоянной):

5. Изменение энтропии одного моля идеального газа при переходе системы из состояния 1 в состояние 2:

6. Аддитивность энтропии:

.

7. Связь между энтропией и статистическим весом (формула Больцмана): ,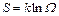

где Ω – статистический вес.

Примеры решения задач

Задача 1. Цикл состоит из двух изохор и двух адиабат. Отношение наибольшего объема газа к наименьшему в цикле равно 8. Рабочим веществом является одноатомный идеальный газ. Определить КПД цикла.

Дано: Решение:

i = 3

 

 

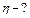
КПД тепловой машины определяется отношением работы за цикл к количеству теплоты, получаемому рабочим телом за цикл:

.

Применим первый закон термодинамики для адиабатных процессов. С учетом выражения для изменения внутренней энергии и определения адиабатного процесса получаем

,

.

В данном цикле работа равна алгебраической сумме работ, выполняемых системой в двух адиабатных процессах . В изохорных процессах 2-3 и 4-1 работа не совершается.

Для процесса 4-1 применим уравнение изохорного процесса:

.

Так как р₁ > р₄, то T₁ > T₄. Газ получает количество теплоты от нагревателя. Это количество теплоты, согласно первому закону термодинамики, равно

.

Для КПД цикла получаем

.

Применим уравнение Пуассона для процессов 3-4 и 1-2. Применим уравнение изохорного процесса для процессов 4-1 и 2-3. Получим систему из четырех уравнений:

, .

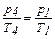Решая систему уравнений, получаем

.

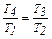Таким образом, КПД цикла

.

Применим уравнение Пуассона в параметрах ТV для процесса 1-2:

Окончательное выражение для КПД цикла:

.

Правая часть уравнения является безразмерной.

Учитывая, что для одноатомного идеального газа i = 3, γ = 5/3, производим вычисления:

.

Ответ: 0,75 (75 %).

 

Задача 2. Азот совершает цикл Карно. Определить КПД цикла, если при адиабатном расширении объем газа увеличивается в 3 раза.

Дано: Решение:

КПД цикла Карно .

i = 5 Определим T_х/T_н, воспользовавшись уравнением

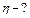Пуассона для процесса адиабатного

расширения газа:

.

Для КПД цикла Карно получаем

.

Правая часть выражения является безразмерной.

Учитывая, что для азота , производим вычисления:

.

Ответ: 0,36 (36 %).

 

Задача 3. Идеальный газ с коэффициентом Пуассона γ=5/3 совершает процесс, в котором давление изменяется по закону p=p₀–αV, где р₀=0,1 МПа, α=50 кПа/м³. При каком значении объема энтропия газа будет максимальной?

Дано: Решение:

Энтропия идеального газа

р_о=0,1 МПа=10⁵Па . (1)

α =50 кПа/м³=5·10⁴ Па Используя уравнения состояния

идеального газа и уравнение про-

цесса, получим зависимость T(V):

. (2)

Подставив (2) в (1), получим зависимость энтропии газа от объема:

.

 

Объем V₀, соответствующий максимуму энтропии, найдем из условий

Этот объем .

Проверка размерности: .

Вычисления: .

Ответ: 1,25 м³.

 

Задача 4. Во сколько раз следует изотермически увеличить объем идеального газа в количестве 3 моль, чтобы его энтропия увеличилась на 25 Дж/К?

Дано: Решение:

ν = 3 моль Для обратимого процесса ,

∆S = 25 Дж/К где .

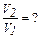
Так как процесс изотермический, то для идеального газа , а элементарная работа равна

.

Изменение энтропии для изотермического процесса будет равно

.

Из последнего соотношения находим

.

Показатель экспоненты – величина безразмерная.

Вычисления: .

Ответ: .

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: