 |
III. Первый закон термодинамики
|
|
|
|
1. Первый закон термодинамики:
,
где δ Q – элементарное количество теплоты, сообщенное термодинамической системе;
dU – бесконечно малое изменение внутренней энергии термодинамической системы;
δA – элементарная работа, совершенная термодинамической системой.
2. Количество теплоты, полученное или отданное системой в процессе,
,
где T1 и T2 – температуры начального и конечного состояния газа;
v – количество молей газа; 
– молярная теплоемкость газа в процессе.
3. Внутренняя энергия идеального газа
.
Изменение внутренней энергии идеального газа в процессе:
.
4. Элементарная работа газа (работа газа при равновесном, бесконечно малом изменении объема)
.
Работа газа в процессе
,
где V1 и V2 – объемы начального и конечного состояния газа.
5. Теплоемкости идеального газа при постоянном объеме и постоянном давлении:
, 
.
6. Соотношение Майера:
.
7. Уравнение адиабатного (происходящего без теплообмена) процесса:
,
где 
– коэффициент Пуассона.
8. Уравнение политропного (происходящего при постоянной теплоемкости) процесса:
,
где n – показатель политропы.
Примеры решения задач
Задача 1. Газообразный водород, находившийся при нормальных физических условиях в закрытом сосуде объемом 5,0 л, охладили на 55 К. Определить приращение внутренней энергии газа и количество отданного им тепла.
Дано: Решение:
ро= 105 Па Первый закон термодинамики:
То= 273 К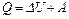 
. (1)
Vo= 5,0·10-3 м3 Для изохорного процесса работа газа
∆Т = – 55 К 
. (2)
Q, ∆E –?
Изменение внутренней энергии идеального газа
. (3)
Уравнение состояния идеального газа:
. (4)
Решая систему уравнений (1) – (4), получаем
.
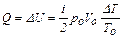Для молекулярного водорода число степеней свободы молекулы i=5.
|
|
|
Проверка размерности:
.
Вычисления:
.
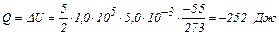Ответ: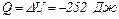 
.
Задача 2. Три моля идеального газа при температуре 300 К изотермически расширили в 4 раза, а затем изохорно нагрели так, что его давление стало равно первоначальному. За весь процесс газу сообщили количество теплоты 67 кДж. Определить коэффициент Пуассона для этого газа.
Дано: Решение:
Т1= 300 К В процессе изотермического расширения
газа из состояния 
в состояние
Q= 6,7·104 Дж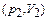 
к газу подводится теплота
.
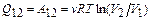В процессе изохорного нагрева к газу подводится количество теплоты
Для нахождения T3 воспользуемся уравнениями изохорного и изотермического процессов:
, 
.
Для T3 получим 
.
Коэффициент Пуассона связан с числом степеней свободы молекулы
газа соотношением 
.
Из этого выражения следует, что 
.
Для 
окончательно получаем
.
При переходе газа из состояния I в состояние III затрачивается количество теплоты
. (1)
Из (1) выразим коэффициент Пуассона
.
Убедимся, что соотношение 
является безразмерной величиной:
.
Вычисления:
.
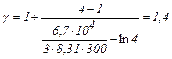Ответ: 1,4.
Задача 3. Объем одного моля идеального газа с коэффициентом Пуассона γ = 5/3 изменяют по закону VT = a, где а – положительная константа. Определить количество теплоты, полученное газом в этом процессе, если его температура возросла на 60 К.
Дано: Решение:
Первый закон термодинамики:
ν = 1 моль . (1)
∆Т = 60 К Бесконечно малое изменение внутренней энергии
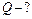
. (2)
Элементарная работа . (3)
Перепишем первый закон термодинамики, выразив изменения термодинамических функций через изменения термодинамических параметров, т.е. подставим уравнения (2) и (3) в уравнение (1):
. (4)
Выразим уравнение процесса в параметрах P и V. Для этого воспользуемся уравнением состояния газа и уравнением процесса, данным в условии задачи:
.
Исключая температуру, получим
. (5)
Выразим число степеней свободы через коэффициент Пуассона:
|
|
|
. (6)
Подставляя уравнения (5) и (6) в уравнение (4) приходим к выражению
. (7)
Интегрируя (7), получаем
.
Проверка размерности:
.
Вычисления:
.
Ответ: 0,25 кДж.
Задача 4. Определить молярную теплоемкость идеального газа в политропном процессе 
, если n = 3, а коэффициент Пуассона этого газа γ = 5/3.
Дано: Решение:
n = 3 Первый закон термодинамики:
γ = 5/3 
. (1)
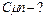Выразив изменения термодинамических функций через изменения термодинамических параметров,
, 
, ,
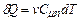и подставив их в уравнение (1), получаем
. (2)
Выразив давление из уравнения процесса, данного в условии, и подставив в уравнение (2), получаем
. (3)
Определим производную 
. Для этого воспользуемся уравнениями политропического процесса и состояния идеального газа и выразим уравнение процесса в параметрах V и T:
. (4)
Дифференцируя (4), получаем 
и подставляем в (3):
.
Проверка размерности:
.
Предельные случаи:
1) при n = 0 получаем р = const, т.е. теплоемкость дли изобарного процесса Cμn = Cμp;
2) при n = γ получаем S = const, т.е. теплоемкость адиабатного процесса Cμn = 0.
Вычисления: 
.
Ответ: 
.
|
|
|
