Задачи для самостоятельного решения

4.1. На рис 4.1 изображены два цикла Карно: 1-2-3-4-1 и 4-3-5-6-4. Процессы 6-4-1 и 2-3-5 адиабатные. Сравнить КПД циклов, если для температур изотермических процессов выполняется равенство Т₁₂–Т₃₄=Т₃₄–Т₅₆.

4.2. Тепловая машина работает по циклу Карно с температурой нагревателя Т_н и температурой холодильника T_х. В первом случае увеличивают только Т_н на ∆Т, а во втором случае температуру холодильника Т_х уменьшают на ∆Т. Сравнить КПД новых циклов.

4.3. На диаграмме рV (рис. 4.2) изображен цикл Карно. При адиабатном расширении газа значение произведения рV уменьшается в 1,5 раза. Определить КПД цикла.

4.4. На диаграмме рV (рис. 4.2) изображен цикл Карно. Определить КПД цикла при условии, что в состояниях 2 и 4 давления газа равны, а отношение объемов V₂/V₄=2.

4.5. На диаграмме рV (рис. 4.2) изображен цикл Карно. Определить КПД цикла при условии, что в состояниях 2 и 4 давления газа равны, а отношение объемов V₂/V₄=4/3.

4.6. На диаграмме рV (рис. 4.2) изображен цикл Карно. Определить КПД цикла при условии, что в состояниях 2 и 4 отношение объемов V₂/V₄=1,5, а отношение давлений р₂/р₄=2.

4.7. На диаграмме рV (рис. 4.2) изображен цикл Карно. Определить КПД цикла при условии, что в состояниях 1 и 3 отношения объемов V₃/V₁=2, а отношение давлений р₁/р₃=1,5.

4.8. Изобразить цикл Карно на диаграмме TS (S – энтропия). По диаграмме определить: а) переданное рабочему телу количество теплоты; б) отданное рабочим телом холодильнику количество теплоты; в) работу, совершенную рабочим телом в цикле.

4.9. Как изменится КПД цикла Карно, если в качестве рабочего тела взять одноатомный газ вместо двухатомного? Относительное изменение объема газа при адиабатном расширении оставить без изменений.

4.10. Тепловая машина работает по циклу Карно. Рабочим веществом машины является идеальный одноатомный газ. При адиабатном расширении газа объем газа увеличивается в 8 раз. Определить КПД машины.

4.11. Тепловая машина работает по циклу Карно. Работа, совершенная рабочим телом при изотермическом расширении, по абсолютной величине в 1,5 раза больше, чем при изотермическом сжатии. Определить КПД машины.

4.12. Тепловая машина работает по циклу Карно (рис. 4.2). Как изменится работа, совершаемая за цикл, если в качестве рабочего тела взять одноатомный газ вместо двухатомного? Состояния 1 и 3 в цикле не изменяются.

4.13. Как изменится работа, совершаемая за цикл Карно, если в качестве рабочего тела взять двухатомный идеальный газ вместо трехатомного? Состояния 2 и 4 в цикле не изменяются (рис. 4.2).

4.14. Идеальный одноатомный газ совершает цикл Карно. Рабо­та, совершаемая газом при изотермическом расширении, равна его работе при адиабатном расширении. Объем газа при изотермическом расширении увеличивается в 2,72 раза. Определить КПД цикла.

4.15. Идеальный одноатомный газ совершает цикл Карно (рис. 4.2). Как изменится количество теплоты, полученное от нагревателя, и количество теплоты, отданное холодильнику, если в ка­честве рабочего тела взять двухатомный газ? Состояния 1 и 3 в цикле не изменяются.

4.16. Идеальный трехатомный газ совершает цикл Карно (рис. 4.2). Как изменится количество теплоты, полученное от нагревателя, и количество теплоты, отданное холодильнику, если в ка­честве рабочего тела взять двухатомный газ? Состояния 2 и 4 в цикле не изменяются.

4.17. Идеальный газ с числом степеней свободы i совершает цикл Карно. Количество теплоты, полученное газом от нагревателя, равно его работе при адиабатном расширении. Объем газа при изотермическом расширении увеличивается от V₁ до V₂. Определить КПД цикла.

4.18. Газ совершает цикл Карно. Абсолютная температура нагревателя в n раз больше температуры холодильника. Нагреватель передал газу количество теплоты Q₁. Определить работу, совершенную газом за цикл.

4.19. В цикле Карно газ отдал холодильнику 3/4 теплоты, полученной от нагревателя. Определить температуру нагревателя, если температура холодильника 300 К.

4.20. Внутри теплоизолированного цилиндра с подвижным поршнем находится газ. При горизонтальном положении цилиндра поршень находится посередине цилиндра. Температура газа по обе стороны поршня одинакова. Когда цилиндр поставили вертикально, поршень сместился под действием силы тяжести. Определить изменение энтропии газа в обеих частях цилиндра. Считать, что поршень не проводит тепло.

4.21. Внутри теплоизолированного цилиндра с подвижным поршнем находится газ. При горизонтальном положении цилиндра поршень находится посередине цилиндра. Температура газа по обе стороны поршня одинакова. Когда цилиндр поставили вертикально, поршень сместился под действием силы тяжести. Определить изменение энтропии газа в обеих частях цилиндра. Считать, что поршень является теплопроводящим.

4.22. Как будет изменяться энтропия термодинамической системы при изотермическом расширении и изотермическом сжатии? Сравнить изменения энтропии системы в этих процессах по абсолютной величине.

4.23. Газ в закрытом теплоизолированном сосуде разделен теплопроводящей перегородкой на две части с разными температурами. В результате теплообмена температура газа в обеих частях становится одинаковой. Сравнить изменения энтропии газа в разных частях сосуда по абсолютной величине?

4.24. Нагретый кусок металла бросают в холодную жидкость. Как изменится энтропия куска металла и жидкости после установления равновесия? Сравнить изменения энтропии куска металла и жидкости по абсолютной величине?

4.25. Холодный кусок металла бросают в горячую воду. Как изменится энтропия куска металла и воды после установления теплового равновесия? Сравнить изменения энтропии куска металла и воды по абсолютной величине?

4.26. Воздушный пузырек всплывает со дна водоема на поверхность. Определить изменение энтропии воздуха в пузырьке. Считать, что температура воды на глубине и у поверхности одинакова.

4.27. На диаграмме рV (рис. 4.3) показаны обратимые процессы перехода идеального газа из состояния 1 в состояние 2 (1-2 изотерма). Доказать, что приращения энтропии газа в процессах 1-2 и 1-3-2 равны.

4.28. 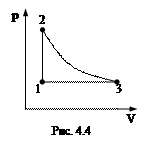На диаграмме рV (рис 4.4) изображены три процесса. Процесс 2-3 – изотермический. Все процессы обратимы. Сравнить приращения энтропии в процессах 1-2 и 1-3.

 

4.29. На диаграмме рV (рис. 4.5) изображены три процесса. Процесс 1-2 – изотермический, 1-3 – адиабатный. Все процессы обратимы. Определить приращения энтропии в процессах 1-2 и 2-3. Значения давлений и объемов в состояниях 1,2,3 считать известными.

 

4.30. На диаграмме рV (рис. 4.6) изображены три процесса. Процесс 1-2 – изотермический, 1-3 – адиабатный. Все процессы обратимы. Сравнить изменения энтропии в процессах 1-2 и 3-2.

 

4.31. На диаграмме рV (рис. 4.7) изображен цикл 1-2-3-4-1, состоящий из двух изобарных и двух изохорных процессов. На каких участках этого цикла происходит увеличение энтропии газа?

 

4.32. На диаграмме рV провести адиабату. Доказать, что состояния газа, которые расположены на диаграмме выше адиабаты, имеют большее значение энтропии, чем состояния, расположенные ниже адиабаты.

4.33. На диаграмме рT изображен цикл, совершенный идеальным газом (рис. 4.8). Определить изменение энтропии газа на участках 1-2, 2-3, 3-1. Значения давления и температуры в состояниях 1, 2, 3 считать известными.

 

4.34. 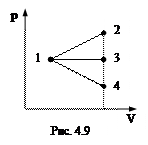На диаграмме рV изображены процессы 1-2, 1-3, 1-4 (рис 4.9). В каком процессе приращение энтропии газа минимально, а в каком – максимально?

 

 

4.35. 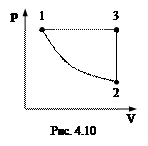На диаграмме рV изображен цикл (рис. 4.10), состоящий из изотермического (1-2), изохорного (2-3), изобарного (3-1) процессов. Определить изменение энтропии газа в этих процессах. Значения давления и объема в состояниях 1, 2, 3 считать известными.

 

4.36. 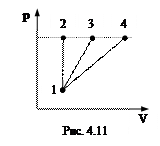Идеальный газ переходит из состояния 1 в состояния 2, 3, 4 (рис. 4.11). Как изменяется энтропия газа в этих процессах? В каком процессе приращение энтропии будет максимально, а в каком минимально?

 

 

4.37. На диаграмме рV изображены процессы идеального газа 1-2, 1-3, 4-5 (рис 4.12).

Процесс 4-5 адиабатный. Сравнить алгебраические (с учетом знака) значения приращения энтропии газа в процессах 1-2 и 1-3.

 

 

4.38. На диаграмме рV изображены процессы идеального газа 1-2, 3-4, 5-6 (рис 4.13). Процесс 5-6 адиабатный. Сравнить приращения энтропии газа в процессах 1-2 и 3-4.

 

4.39. Два моля двухатомного идеального газа переходят из состояния c давлением р и объемом V в состояние c давлением 2р и объемом 2V. Определить изменение энтропии газа.

4.40. В адиабатном процессе объем 2 молей двухатомного газа уменьшили в 2 раза, затем газ при постоянном объеме охладили до начальной температуры. Изобразить процессы на диаграмме рV. Определить изменение энтропии газа.

4.41. Идеальный газ в количестве 2 молей сначала адиабатно сжимается так, что объем уменьшается в 3 раза, затем изотермически расширяется до начального объема. Изобразить процессы на диаграмме рV. Определить изменение энтропии газа.

4.42. Идеальный газ в количестве 3 молей сначала изобарно уменьшает объем в 2 раз, затем изохорно увеличивает давление за счет нагревания в 2 раза. Изобразить процессы на диаграмме рV. Определить изменение энтропии газа.

4.43. В термосе смешивают горячую воду массой 1 кг при температуре 50 ºС с холодной водой такой же массы при температуре 10 ºС. Определить приращение энтропии системы.

 

4.44. На диаграмме рV изображены процессы идеального газа (рис. 4.14) . Газ переходит из состояния 1 в состояние 2 процессами 1-3-2 и 1-4-2. Все процессы обратимы. Показать расчетом, что приращения энтропии газа в процессах 1-3-2 и 1-4-2 равны. Значения давления и объема в состояниях 1,2,3,4 считать известными.

 

4.45. На диаграмме рV изображены процессы идеального газа (рис. 4.15). Процесс 1-2 – изотермический, 1-3 – адиабатный, 3-2 – изобарный. Газ переходит из состояния 1 в состояние 2 процессами 1-2 и 1-3-2. Все процессы обратимы. Показать расчетом, что приращения энтропии газа в обоих случаях равны. Значения давления и объема в состояниях 1,2,3 считать известными.

4.46. Кусок льда массой 100 г нагревают от температуры 250 К до температуры плавления и плавят. Определить приращение энтропии льда.

4.47. Водяной пар массой 100 г при температуре 100 °С превра­щается в воду, которая затем охлаждается до температуры 0 °С. Определить приращение энтропии.

4.48. Температура вещества зависит от энтропии по закону Т=αSⁿ, где α, n – постоянные. Определить теплоемкость С вещества как функцию энтропии S. При каком условии С<0?

4.49. Один моль идеального газа совершает процесс, в котором энтропия газа изменяется в зависимости от температуры по закону S=αТ+С_μVlnТ, где α – постоянная больше нуля; С_μV – молярная теплоемкость газа при постоянном объеме. В начальном состоянии заданы объем V₀ и температура Т₀. Определить зависимость температуры газа от объема.

4.50. Один моль идеального газа совершает процесс, в котором температура газа изменяется в зависимости от объема по закону , где Т₀ – начальная температура газа; V₀ – начальный объем газа, а=const, a>0. Определить зависимость энтропии газа от температуры.

4.51. Идеальный газ с коэффициентом Пуассона γ совершает процесс, в котором давление изменяется в зависимости от объема по закону р=р_о–αV, где р_о и α – положительные постоянные. При каком значении объема энтропия газа будет иметь максимальное значение?

4.52. Один моль идеального газа с известным значением теплоемкости C_μV совершает процесс, в котором энтропия S изменяется в зависимости от температуры по закону S=α/T, где α=const. Выразить теплоемкость газа в этом процессе как функцию температуры. Определить количество теплоты, сообщенное газу, и работу, совершенную газом, при изменении температура газа от T₁ до Т₂.

4.53. Теплоизолированный сосуд разделен перегородкой на две части так, что объем одной из них в 2 раза больше другой. В меньшей части находилось 0,3 моля азота, а в большей части – 0,7 моля кислорода. Температуры газов были одинаковы. Перегородку убрали, и газы перемешались. Определить приращение энтропии системы.

4.54. Процесс расширения двух молей аргона происходит так, что давление увеличивается прямо пропорционально объему. Определить приращение энтропии газа при увеличении его объема в 2 раза.

4.55. На диаграмме рV (рис. 4.16) изображен обратимый цикл, который совершает идеальный газ. Процесс 1-3 адиабатный. Значения давления объема и температуры в состояниях 1, 2, 3 считать известными. Определить работу газа за цикл и КПД цикла как функции температур Т₁, Т₂, Т₃.

 

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Савельев, И.В. Курс физики. В 3т. Т.1. Механика. Молекулярная физика / И.В. Савельев. – М.: Наука, 1989.

2. Иродов, И.Е. Физика макросистем. Основные законы / Е.И. Иродов. – М.; СПб.: Физматлит, 2001.

3. Волков, В.Н. Физика. В 3т. Т.1. Механика. Основы молекулярной физики и термодинамики / В.Н. Волков, Г.И.Рыбакова, М.Н. Шипко; Иван. гос. ун-т. – Иваново, 1993.

4. Детлаф, А.А. Курс физики. В 3т. Т.1. Механика. Молекулярная физика / А.А. Детлаф, В.М. Яворский, Л.Б. Милковская. – М.: Высш. шк., 1977.

5. Зисман, Г.А. Курс физики. В 3т. Т.1. Механика. Молекулярная физика / Г.А. Зисман, О.М. Тодес. – М.: Наука, 1974.

⇐ Предыдущая1234567

Поделиться:

Воспользуйтесь поиском по сайту: