 |
Выбор меры центральной тенденции
|
|
|
|
Вычисление моды, медианы или среднего – чисто техническая процедура. Однако выбор из этих трех мер и их интерпретация зачастую требуют определенного размышления. В процессе выбора следует установить следующее:
– в малых группах мода может быть совершенно нестабильной. Например, мода группы: 1, 1, 1, 3, 5, 7, 7, 8 равна 1; но если одна из единиц превратится в нуль, а другая – в два, то мода будет равна 7;
– на медиану не влияют величины “больших” и “малых” значений. Например, в группе из 50 значений медиана не изменится, если наибольшее значение утроится;
– на величину среднего влияет каждое значение. Если одно какое-нибудь значение меняется на c единиц,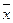 
изменится в том же направлении на c/n единиц;
– некоторые множества данных не имеют центральной тенденции, что часто вводит в заблуждение при вычислении только одной меры центральной тенденции. Особенно это справедливо для групп, имеющих более чем одну моду;
– когда считают, что группа данных является выборкой из большой симметричной группы, среднее выборки, вероятно, ближе к центру большой группы, чем медиана и мода.
Все средние характеристики дают общую характеристику ряда результатов измерений. На практике нас часто интересует, как сильно каждый результат отклоняется от среднего значения. Однако легко можно представить, что две группы результатов измерений имеют одинаковые средние, но различные значения измерений. Например, для ряда 3, 6, 3 – среднее значение 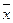= 4; для ряда 5, 2, 5 – также среднее значение 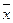= 4, несмотря на существенное различие этих рядов.
Поэтому средние характеристики всегда необходимо дополнять показателями вариации, или колеблемости.
Характеристики вариации
|
|
|
К характеристикам вариации, или колеблемости, результатов измерений относят размах варьирования, дисперсию, среднее квадратическое отклонение, коэффициент вариации, стандартную ошибку средней арифметической.
Самой простой характеристикой вариации является размах варьирования. Его определяют как разность между наибольшим и наименьшим результатами измерений. Однако он улавливает только крайние отклонения, но не отражает отклонений всех результатов.
Чтобы дать обобщающую характеристику, можно вычислить отклонения от среднего результата. Например, для ряда 3, 6, 3 значения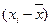 
будут следующими: 3 – 4 = – 1; 6 – 4 = 2; 3 – 4 = – 1. Сумма этих отклонений (– 1) + 2 + (– 1) всегда равна 0. Чтобы избежать этого, значения каждого отклонения возводят в квадрат: (– 1)2 + 22 + (– 1)2 = 6.
Значение 
делает отклонения от средней более явственными: малые отклонения становятся еще меньше (0,52=0,25), а большие – еще больше (52 = 25). Получившуюся сумму 
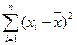называют суммой квадратов отклонений. Разделив эту сумму на число измерений, получают средний квадрат отклонений, или дисперсию. Она обозначается s2 и вычисляется по формуле:
. (2.3)
Если число измерений не более 30, т.е. n ≤ 30, используется формула:
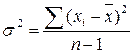. (2.4)
Величина n – 1 = k называется числом степеней свободы, под которым подразумевается число свободно варьирующих членов совокупности. Установлено, что при вычислении показателей вариации один член эмпирической совокупности всегда не имеет степени свободы.
Эти формулы применяются, когда результаты представлены неупорядоченной (обычной) выборкой.
Из характеристик колеблемости наиболее часто используется среднее квадратическое отклонение, которое определяется как положительное значение корня квадратного из значения дисперсии, т.е.:
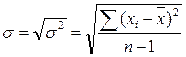. (2.5)
Среднее квадратическое отклонение или стандартное отклонение характеризует степень отклонения результатов от среднего значения в абсолютных единицах и имеет те же единицы измерения, что и результаты измерения.
|
|
|
Однако для сравнения колеблемости двух и более совокупностей, имеющих различные единицы измерения, эта характеристика не пригодна.
Коэффициент вариации определяется как отношение среднего квадратического отклонения к среднему арифметическому, выраженное в процентах. Вычисляется он по формуле:
.
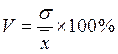В спортивной практике колеблемость результатов измерений в зависимости от величины коэффициента вариации считают небольшой
(0 – 10 %), средней (11 – 20 %) и большой (V > 20 %).
Коэффициент вариации имеет большое значение в спортивной метрологии, т. к., будучи величиной относительной (измеряется в процентах), позволяет сравнивать между собой колеблемость результатов измерений, имеющих различные единицы измерения. Коэффициент вариации можно использовать лишь в том случае, если измерения выполнены в шкале отношений.
|
|
|
