 |
Показатель точности оценки параметров
|
|
|
|
Сама по себе абсолютная величина выборочной ошибки как показатель именованный мало пригодна для случаев сравнительной оценки точности, с какой определены средние результаты наблюдений по отношению их к генеральным параметрам, в случае, если средние с их ошибками выражены в разных единицах измерения.
Чтобы получить определенное представление о точности, с какой определен тот или иной результат, принято использовать так называемый показатель точности (CS). Когда известно значение коэффициента вариации V %, показатель точности можно определить по следующей формуле:
 .
.
Известно, что под точностью определения выборочной средней понимается степень приближения ее к средней генеральной совокупности. Чем точнее определен средний результат, тем меньше будет CS и наоборот, при менее точном среднем результате показатель CS окажется больше. Точность считается достаточной, если CS не превышает 5 %. Если проводят очень важные испытания, связанные с жизнью человека, то CS не превышает 3 %.
Порядок работы на II этапе
1. Ознакомиться с ситуацией и организацией игры на II этапе.
2. Ознакомиться с теоретическими сведениями.
3. Ознакомиться с образцом отчета о работе на II этапе.
4. Рассчитать основные статистические характеристики выборок.
5. Построить основные графики вариационного ряда (полигон распределения, гистограмма распределения) для выборки А.
6. Оформить отчет о проделанной работе (по образцу, приведенному далее).
Отчет
о работе на II этапе игры
(образец)
Тема: Математические методы статистической обработки результатов измерений в спорте.
Цели:
1. Ознакомиться с наиболее распространенными методами статистической обработки результатов измерений в физическом воспитании и спорте.
|
|
|
2. Приобрести навыки расчета основных статистических характеристик выборки.
3. Научиться строить основные графики вариационного ряда (полигон распределения, гистограмма распределения).
Вопросы:
1. Предмет математической статистики.
2. Этапы статистического обследования.
3. Дискретные и непрерывные ряды.
4. Выборочная и генеральная совокупности. Объем выборки.
5. Что называют ранжированием ряда?
6. Полигон и гистограмма распределения.
7. Основные статистические характеристики центра ряда.
8. Характеристики вариации.
9. Понятие репрезентативности выборочных показателей, ошибки репрезентативности.
Статистическая обработка результатов измерений,
проведенных в группе «тренера» Иванова И.
(Ф.И.О. студента, пишущего отчет)
Расчет основных статистических характеристик выборки А:
| № п/п |  , мс , мс
| 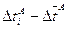 , мс , мс
| 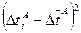 , мс2 , мс2
|
| 1. | -12 | ||
| 2. | |||
| 3. | -34 | ||
| 4. | |||
| 5. | |||
| 6. | -21 | ||
| 7. | -14 | ||
| 8. | |||
| 9. | |||
| 10. | -11 | ||
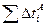 = 1648 мс = 1648 мс
|  = 4790 мс2 = 4790 мс2
|
Запишем выборку А в порядке возрастания, т.е. ранжированный ряд и найдем моду и медиану.
131, 144, 151, 153, 154, 168, 168, 182, 189, 208.
Мода = 168 мс.
Медиана = 161 мс.
Среднее арифметическое значение выборки А:
 мс.
мс.
Дисперсия:
 мс2.
мс2.
Среднее квадратическое (стандартное) отклонение:
 мс.
мс.
Стандартная ошибка средней арифметической:
 мс.
мс.
Коэффициент вариации:
 .
.
Размах варьирования R = 208 – 131 = 77 мс
Графическое представление
Запишем ранжированный ряд:
131, 144, 151, 153, 154, 168, 168, 182, 189, 208.
Т.к. n = 10, по таблице 2.2 находим число интервалов: k = 4.
Шаг интервала:  мс.
мс.
Примечание: во избежание ошибок при составлении вариационного ряда шаг интервала надо использовать без округлений или округлять только в большую сторону.
Заполним таблицу «Вариационный ряд результатов измерений».
|
|
|
Столбец 1. Записываем порядковые номера интервалов.
Столбец 2. Нижнюю границу 1-го интервала выбираем равной xmin=131; прибавляем шаг интервала: 131 + 19,25 = 150,25 – верхняя граница 1-го интервала (она же нижняя граница 2-го интервала) и т.д.
Столбец 3. Частота интервала равна количеству значений в выборке, которые попали в обозначенный интервал. Первое число включаем в 1-й интервал. Если какое-либо число попало на границу между интервалами, его следует включать в меньший по порядку интервал, например, число на границе 1-го и 2-го интервалов включается в 1-й интервал. Последнее число должно оказаться в последнем интервале. Сумма частот всех интервалов должна быть равна объему выборки.
Вариационный ряд результатов измерений
| № интервала | Границы интервала | Частота |
| 131 – 150,25 | ||
| 150,25 – 169,5 | ||
| 169,5 – 188,75 | ||
| 188,75 – 208 |
Полигон распределения

Гистограмма распределения

131 150,25 169,5 188,75 208
Расчет основных статистических характеристик выборки Б:
| № п/п |  , мс , мс
|  , мс , мс
| 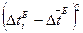 , мс2 , мс2
|
| 1. | -7 | ||
| 2. | |||
| 3. | -34 | ||
| 4. | -17 | ||
| 5. | |||
| 6. | -16 | ||
| 7. | |||
| 8. | |||
| 9. | |||
| 10. | -3 | ||
 = 1565 мс = 1565 мс
|  = 3293 мс2 = 3293 мс2
|
Запишем выборку Б в порядке возрастания, т.е. ранжированный ряд и найдем моду и медиану.
123, 140, 141, 150, 154, 162, 165, 167, 173, 190.
Моды нет.
Медиана = 158 мс.
Среднее арифметическое значение выборки Б:
 мс.
мс.
Дисперсия:
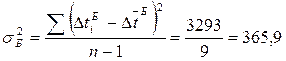 мс2.
мс2.
Среднее квадратическое отклонение:
 мс.
мс.
Стандартная ошибка средней арифметической:
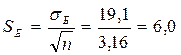 мс.
мс.
Коэффициент вариации:
 .
.
Размах варьирования R = 190 – 123 = 67 мс
Графическое представление
Запишем ранжированный ряд:
123, 141, 142, 150, 154, 162, 163, 167, 173, 190.
Шаг интервала:  мс.
мс.
Вариационный ряд результатов измерений
| № интервала | Границы интервала | Частота |
| 123 – 139,75 | ||
| 139,75 – 156,5 | ||
| 156,5 – 173,25 | ||
| 173,25 – 190 |
Полигон распределения


Гистограмма распределения

123 139,75 156,5 173,25 190
Расчет основных статистических характеристик выборки В:
| № п/п |  , уд. , уд.
|  , уд. , уд.
|  , уд.2 , уд.2
|
| 1. | -1 | ||
| 2. | |||
| 3. | |||
| 4. | -21 | ||
| 5. | -1 | ||
| 6. | |||
| 7. | |||
| 8. | -5 | ||
| 9. | -9 | ||
| 10. | |||
 = 705 уд. = 705 уд.
|  = 1067 уд.2 = 1067 уд.2
|
|
|
|
Запишем выборку В в порядке возрастания, т.е. ранжированный ряд и найдем моду и медиану.
50, 62, 66, 70, 70, 71, 74, 74, 75, 93.
Мода1 = 70 уд. Мода2 = 74 уд.
Медиана = 70,5 уд.
Среднее арифметическое значение выборки В:
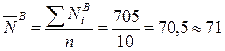 уд.
уд.
Дисперсия:
 уд2.
уд2.
Среднее квадратическое отклонение:
 уд.
уд.
Стандартная ошибка средней арифметической:
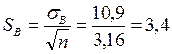 уд.
уд.
Коэффициент вариации:
 .
.
Размах варьирования R = 93 – 50 = 43 уд.
Графическое представление
Запишем ранжированный ряд:
50, 62, 66, 70, 70, 71, 74, 74, 75, 93.
Шаг интервала: 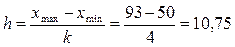 уд.
уд.
Вариационный ряд результатов измерений
| № интервала | Границы интервала | Частота |
| 50 – 60,75 | ||
| 60,75 – 71,5 | ||
| 71,5 – 82,25 | ||
| 82,25 – 93 |
Полигон распределения
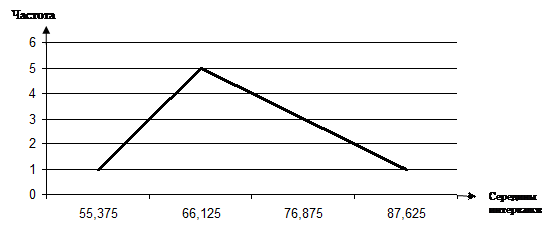
Гистограмма распределения


50 60,75 71,5 82,25 93
|
|
|


