 |
Пути повышения надежности теста
|
|
|
|
Надежность тестов может быть повышена до определенной степени путем:
а) более строгой стандартизации тестирования;
б) увеличения числа попыток;
в) увеличения числа оценщиков (судей, экспертов) и повышения согласованности их мнений;
г) увеличения числа эквивалентных тестов;
д) лучшей мотивации испытуемых.
Среди упомянутых путей следует выделить отличающееся высокой эффективностью повышение надежности путем увеличения длины теста. Удлинение теста достигается увеличением числа попыток, числа испытуемых или того и другого вместе.
При увеличении длины теста в m раз надежность теста rtt возрастает до величины r0tt, приближенно равной:

Из этой формулы можно определить, во сколько раз нужно увеличить тест, чтобы получить желаемую надежность r0tt:
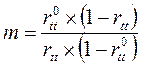
Очевидно, что целесообразно повышать длину теста лишь при не слишком больших величинах m. При значениях m, трудно реализуемых практически, лучше ненадежный тест заменить другим, более надежным.
Порядок работы на III этапе
Отчет
о работе на III этапе игры
(образец)
Тема: Оценка надежности теста для контроля за развитием скоростных качеств.
Цели:
1. Ознакомиться с основами теории корреляции.
2. Ознакомиться с основами теории проверки статистических гипотез.
3. Ознакомиться с основами теории надежности тестов.
4. Приобрести навыки вычисления показателя надежности (стабильности) теста.
Вопросы:
1. Основы теории корреляции:
1.1. Функциональная зависимость.
1.2. Статистическая зависимость.
1.3. Основные задачи теории корреляции.
1.4. Корреляционное поле.
1.5. Формы корреляционной зависимости.
1.6. Коэффициент корреляции.
1.7. Направленность корреляционной взаимосвязи.
|
|
|
1.8. Коэффициент корреляции Бравэ-Пирсона.
2. Статистические гипотезы.
2.1. Определение статистической гипотезы, примеры.
2.2. Критерии проверки статистических гипотез.
2.3. Ошибки первого и второго рода.
2.4. Уровень значимости.
3. Основы теории надежности тестов.
3.1. Показатель надёжности тестов.
3.2. Стабильность тестов.
3.3. Согласованность тестов.
3.4. Эквивалентность тестов.
3.5. Пути повышения надежности тестов.
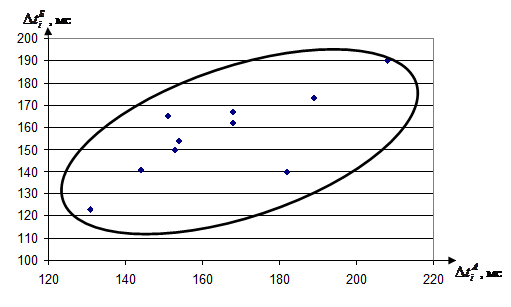
Корреляционное поле
Представим взаимосвязь результатов измерения теста А и ретеста Б в виде графика, для чего в прямоугольной системе координат построим корреляционное поле. Результаты теста А будем откладывать по оси абсцисс, а результаты теста Б по оси ординат.
Для наглядности построим график в системе координат, смещенной относительно нуля. Выберем масштаб, позволяющий нанести на график все исходные данные. М: 1 см ≡ 10 мс.
Так как результаты тестирования измерены в шкале отношений, а число попыток (исходное и повторное тестирования) равно двум, для оценки надежности (стабильности) теста выберем парный коэффициент корреляции Бравэ-Пирсона rАБ, рассчитываемый по формуле:
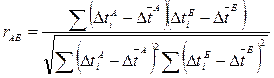
Пользуясь данными, полученными на I и II этапах игры, составим таблицу 3.2 для расчета показателя надежности (стабильности) теста.
Таблица 3.2 – Расчет показателя надежности теста
| № п/п | тест А,  , мс , мс
| Ретест Б, 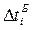 , мс , мс
| 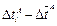 , мс , мс
| 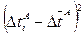 ,
мс2 ,
мс2
| 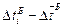 , мс , мс
| 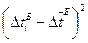 ,
мс2 ,
мс2
|  ×
× ×
× 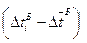 , мс2 , мс2
|
| -12 | -7 | ||||||
| -34 | -34 | ||||||
| -17 | -289 | ||||||
| -21 | -16 | ||||||
| -14 | -112 | ||||||
| -11 | -3 | ||||||
| S=1648 | S=1565 | S=4790 | S=3293 | S=3056 |
Подсчитаем величину показателя надежности (стабильности):
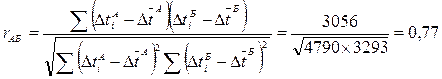 .
.
Для оценки надежности теста воспользуемся таблицей 3.3.
|
|
|
Таблица 3.3 – Качество надежности теста
| Величина показателя надежности | 0,99 – 0,95 | 0,94 – 0,90 | 0,89 – 0,80 | 0,79 – 0,70 | 0,69 и ниже |
| Надежность | Отлич-ная | Хоро-шая | Удовлет-воритель-ная | Сомни-тельная | Плохая |
Вывод: Так как 0,70 < ½ rАБ ½ < 0,79, надежность (стабильность) теста сомнительная.
Оценим статистическую достоверность показателя надежности.
Выдвинем две статистические гипотезы:
– нулевую – Н0: предполагаем, что показатель надёжности теста статистически недостоверен (rген = 0);
– конкурирующую – Н1: предполагаем, что показатель надёжности теста статистически достоверен (rген > 0).
Для сравнения выдвинутых гипотез найдём критическое значение коэффициента корреляции. По таблице критических точек коэффициента корреляции (Приложение 1) для односторонней критической области при n = 10 и α = 0,05 находим rкрит = 0,549. Сравниваем rнабл с rкрит.
Вывод: Так как  (0,77) > rкрит (0,549), показатель надежности (стабильности) теста для данной группы «спортсменов» статистически достоверен с вероятностью 0,95.
(0,77) > rкрит (0,549), показатель надежности (стабильности) теста для данной группы «спортсменов» статистически достоверен с вероятностью 0,95.
Тест с надежностью ниже удовлетворительной недопустимо использовать для контроля развития у спортсменов скоростных качеств. Поэтому повысим надежность теста до удовлетворительного уровня (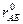 = 0,80) путем его удлинения.
= 0,80) путем его удлинения.
Определим, во сколько раз надо увеличить число испытуемых или число попыток при тестировании:
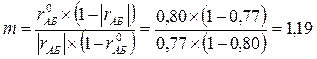 .
.
Требуемое число испытуемых равно 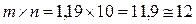 человек.
человек.
Требуемое число попыток получим 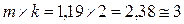 .
.
|
|
|


