 |
Модели с дискретным временем
|
|
|
|
Принцип построения моделей этого типа основан на анализе в первую очередь возрастной структуры популяции, соотношения остатка и пополнения и периодичности нереста. На этом принципе основаны модели А. Н. Державина (1922), Н. Л. Чугунова (1935), Роллефсена (Rollefsen, 1935), Г. Н. Монастырского (1940, 1952), Т. Ф. Дементьевой (1952 и др.), Г. В. Никольского (1961а, 1963 и др.), Ю. Е. Лапина (1961) и многие другие. Первоначально эти модели использовались непосредственно в прогностических целях; в последнее время сделаны попытки их программирования и использования для расчетов на ЭВМ (Меншуткин, 1964г 1964а, 1965, 1971). Первую модель этого типа предложил, как известно А. Н. Державин (1922) для расчета численности куринского стада севрюги. Формула для расчета запаса, основанная на этой модели, имела следующий вид:
 (18)
(18)
где:
Rn- запас рыбы к началу года п;
z - предельный возраст рыбы;
Рn, Рn+1, Рn+2 - уловы за ряд лет;
х - процент сеголетков в улове;
x1 - то же, годовиков;
x 2 - то же, двухгодовиков и т. д.
В своем построении А. Н. Державин исходил из постоянства возрастного состава, что может быть принято при незначительных флюктуациях численности поколений и при стабильной интенсивности рыболовства. В отношении рыб со значительными колебаниями урожайности допущение постоянства возрастного состава невозможно, и в последующих моделях (Чугунов, 1935; Монастырский, 1940) принимался уже фактически наблюденный за каждый год возрастной состав. О необходимости такой поправки к его формуле говорил в своей работе и сам Державин Н. Л. Чугунов (1935) видоизменил формулу, предложенную Державиным, введя поправку на специфичность возрастного состава стада в каждом конкретном году. Таким образом, эта формула стала пригодной и для рыб со значительными колебаниями урожайности по годам. Формула Н. Л. Чугунова имеет следующий вид:
|
|
|
 (19)
(19)
где:
Σ - промысловый запас;
а3, b4, c5, хdn и т. д.- количество рыб разных возрастных групп.
Обнаружение на чешуе и отолитах рыб нерестовых отметок позволило в математических моделях нерестовой популяции отчленить остаток от пополнения. Это впервые сделали Роллефсен (1935, 1939) в отношении трески и Г. Н. Монастырский (1940) в отношении воблы. Формула, принятая Монастырским применительно к вобле, имеет следующий вид:
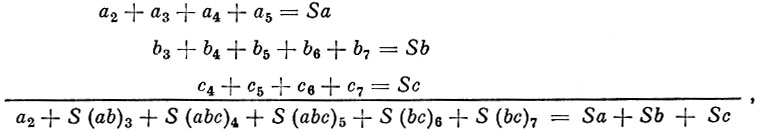 (20)
(20)
где а2-а5 - возрастной состав пополнения;
b3-b7 - возрастной состав повторно нерестующих рыб;
c4-с7 - возрастной состав особей, пропустивших один нерестовый сезон.
Мы не будем останавливаться на рассмотрении многочисленных структурных математических моделей, использованных как отечественными, так и зарубежными исследователями. Обзор их дан в работах С. В. Аве-ринцева (1948) и Г. Н. Монастырского (1940, 1952). Несомненно, что анализ возрастного состава нерестовой популяции останется и впредь одним из важных показателей, по которому наряду с другими показателями можно судить о состоянии стада промысловой рыбы.
Изложенный принцип построения моделей был использован Ю. Е. Лапиным (1961) и мною. В виде блок-схемы предложенная мною модель может быть представлена в следующем виде (рис. 104).

Рис. 104. Блок-схема модели динамики популяций (по Никольскому, 1963)

Рис. 105. Блок-схема возрастного состава нерестового стада трески (по Никольскому 1968а): 1 - непостоянно действующая связь; 2 - постоянно действующая связь, но с переменной интенсивностью. R - пополнение; St - остаток; R+St - нерестовое стадо; М - общая смертность
Математическая интерпретация этой модели* - аналитическое выражение алгоритма перехода от одного состояния к другому - может быть выражена следующим образом:
* (Аналитическое выражение алгоритма этой модели любезно предложено мне В. В. Меншуткиным.)
|
|
|
 (21)
(21)
где NTK- численность возрастной группы в возрасте К в момент времени Т;
FT- вылов (или общая смертность);
RT- пополнение;
VK- возрастная структура пополнения.
Следующий этап в разработке математических моделей с дискретным временем - это включение в них элемента саморегулирования, т. е. обратной связи стадо - пополнение. Если в моделях Ю. Е. Лапина (1961) и моих (Никольский, 1960, 1961, 1963) пополнение обусловлено только внешними причинами, не зависимыми от численности стада, то в последней модели (Меншуткин, 1965) уже в некоторой степени введен элемент саморегулирования. Учтено также запаздывание реакции пополнения на изменения, происходящие в стаде в связи с возрастом полового созревания. От предыдущей блок-схема этой модели отличается "подвижностью" возрастного состава пополнения. Основные же различия связаны с сопряженностью стада и пополнения.
Конечно, все эти модели еще очень примитивны. Однако их программирование и изучение на ЭВМ, проведенное В. В. Меншуткиным (1964, 1971), показывает, что широкое использование ЭВМ в популяционных исследованиях и в организации рыбного хозяйства - дело ближайшего будущего.
Приложением рассмотренной блок-схемы к конкретному виду рыбы может служить составленная нами (Никольский, 1968а) блок-схема динамики возрастного состава нерестового стада аркто-норвежской трески.
Она, естественно, охватывает лишь часть процесса динамики стада, но на ней отчетливо видны параметры "эластичности" возрастной структуры нерестового стада (рис. 105).
Программирование и исследование на ЭВМ предложенных нами моделей, несмотря на их примитивность, есть необходимый этап в разработке методики использования ЭВМ в популяционном анализе.
Результаты исследования этих моделей на ЭВМ могут быть перенесены на конкретные популяции рыб лишь в той степени, в какой конкретные свойства популяции отражены в исследованных моделях (Меншуткин, 1964, 1965, 1971). Однако проведенный анализ позволяет отработать как методику моделирования, так и формы реализации моделей для получения необходимых практических результатов. Практически "емкость" ЭВМ значительно больше того количества и ассортимента материала, который могут дать для переработки биологи. Несомненно, что структурные модели с дискретным временем, являющиеся значительно более емкими в отношении биологического материала, имеют большие преимущества для использования ЭВМ перед моделями первого типа.
|
|
|
|
|
|


