 |
Задача с критерием оптимальности на минимум затрат.
|
|
|
|
сj - себестоимость единицы j-й продукции.
Модель с крит-ем оптимальности — минимум затрат на весь объем выпуска:
Чтобы значение критерия оптимальности не “скатывалось” до нуля, необходимо ограничить снизу (т.е. ввести ограничение вида >) решение. Такими условиями, как мы уже знаем, являются условия по выполнению директивно заданного плана производства.
Правильный выбор наилучшего варианта из нескольких допустимых возможен при следующих постановках задачи:
— максимизация результата (эффекта) при фиксированном уровне затрат (ресурсов);
— минимизация затрат при фиксированном уровне результатов.
Рассмотрим модель задачи на минимум затрат при фиксированных планах производства, предположив, что каждый вид продукции производится лишь одним технологическим способом:
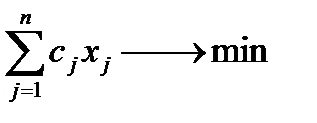
Любой сверхплановый выпуск, даже самых скромных размеров, увеличит значение критерия оптимальности. Ясно, что наименьший уровень затрат возможен лишь при строгом выполнении плановых заданий, т.е. при Xj = bj. Тем самым данная модель теряет смысл, так как в подобной задаче нечего искать. Оптимальный план известен: он задается числами bj.
Однако это не значит, что при отсутствии нескольких способов производства одноименной продукции постановка задачи на минимум затрат бессмысленна. Нужно лишь задать результат с меньшей степенью подробности, нежели искомые величины:
Переменные XjS детализированы и по видам продукции j и по способам производства s, а плановые задания bj - лишь по продукции. Поэтому оптимизация осуществляется подбором разных величин Xjs в рамках единой фиксированной величины bj, т.е. подбором сочетания различных технологий для выпуска данной j- й продукции.
|
|
|
Рассмотрим еще один подход, позволяющий ограничить решение снизу в задаче на минимум затрат. Обозначим в данном случае через pj цены на продукцию j-го вида, а через P - план по валовой продукции. Заменим детальные ограничения Xj > bj агрегированным ограничением Σ Pj Xj >P (если вернуться к первоначальному определению величин Pj, то Р - запланированный уровень валового дохода от выпуска продукции).
Тогда модель на минимум затрат в случае, когда каждый вид продукта производится лишь одним технологическим способом, запишется так:
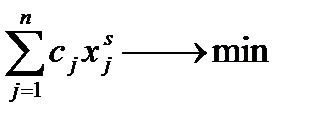
Отметим одну важную особенность рассмотренных моделей (всех). Ограничения вида “>“ по объему производства или валовому доходу могут потребовать расхода одного или нескольких ресурсов, превышающего их наличный запас, учитываемый в ограничениях вида “<“. Противоречивость рассматриваемых ограничений при решении задачи с конкретными значениями bi и bj может привести к тому, что область допустимых решений окажется пустой и оптимизационная задача будет неразрешимой.
Вопрос 11.
Представим себе любую линейную оптимизационную задачу и кратко напомним основные особенности симплекс-метода. Его идея состоит в переходе от одного базисного (опорного) плана к другому таким образом, что линейная форма улучшается на каждом шаге и достигает экстремума. Переход происходит по вершинам выпуклого многогранника условий в n -мерном пространстве, причем на каждом шаге переход осуществляется в соседнюю вершину. При нахождении в такой вершине проводится проверка плана на оптимальность. Линейная форма (гиперплоскость) делит всё пространство на две части. Вершинам, находящимся в верхней части, соответствуют отрицательные элементы целевой строки, а вершинам из нижней части — положительные. Переход осуществляется только в соседние вершины из верхнего полупространства до тех пор пока в нем не останется ни одной вершины. Переход проводится в ту вершину, которой соответствует максимальный по абсолютной величине из отрицательных элементов целевой строки. Если на последнем шаге линейная форма имеет более одной общей точки с выпуклым многогранником условий, то имеется множество оптимальных планов. Итак, отличительной особенностью метода является движение к оптимуму по вершинам. Все отмеченные выше особенности можно проследить на рис.2.1, где представлен многогранник условий ОАВСD и показаны положения линейной формы при последовательном движении по вершинам О, А и В (точка оптимума).
|
|
|
На данном рисунке хорошо видно, что для задач линейного программирования характерно следующее:
| О |
| A |
| B |
| C |
| D |
| x1 |
| x2 |
Рис 2.1
1.Множество допустимых решений выпукло и имеет конечное число крайних точек (вершин);
2.Целевая функция представляет собой гиперплоскость. Гиперплоскости, соответствующие разным значениям целевой функции параллельны.
|
|
|
3.Локальный оптимум является одновременно и глобальным оптимумом.
4.Если целевая функция ограничена на множестве допустимых решений, то оптимум достигается по крайней мере в одной из крайних точек вершин) этого множества, и, начав с произвольной вершины, перемещаясь затем на каждом шаге в соседнюю, достигаем точки оптимума за конечное число шагов.
В задачах нелинейного программирования эти условия полностью или частично не соблюдаются. Рассмотрим ряд случаев.
Случай 1. Пусть при линейных ограничениях имеем нелинейную, сепарабельную целевую функцию вида
с 1 (x 1- x 1°) 2 + с 2 (x 2- x 2°) 2® min,
| О |
| A |
| x2 |
| x1 |
| • |
| • |
| xo2 |
| xo1 |
| Рис. 2.2 |
|
|
|
Итак, в данном случае невыполнение условия 2 влечет за собой и невыполнение условия 4. Оптимум достигается не на вершине, а на грани, откуда следует, что перебор вершин недостаточен.
Из рис. 2.2 видно, что при смягчении заданий по выпуску продукции x 1° и x 2°можно уменьшить сумму штрафа вплоть до нуля. Так, сместив центр эллипса вовнутрь многогранника условий, получим, что оптимум достигается во внутренней точке.
Случай 2. При иной конфигурации области допустимых значений, описываемой как и ранее линейными ограничениями, и при опять-таки нелинейной сепарабельной целевой функции вида
p 1 (x 1- x 1°) 2 + p 2 (x 2- x 2°) 2® max,
получим рис.2.3.
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAY6QEqsQA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPS2vCQBC+F/wPywje6iaCraSuEgJSkfbg4+JtzI5J aHY2za5J7K/vFgre5uN7znI9mFp01LrKsoJ4GoEgzq2uuFBwOm6eFyCcR9ZYWyYFd3KwXo2elpho 2/OeuoMvRAhhl6CC0vsmkdLlJRl0U9sQB+5qW4M+wLaQusU+hJtazqLoRRqsODSU2FBWUv51uBkF u2zzifvLzCx+6uz945o236fzXKnJeEjfQHga/EP8797qMD9+hb9nwgVy9QsAAP//AwBQSwECLQAU AAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnht bFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVs c1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4 bWwueG1sUEsBAi0AFAAGAAgAAAAhAGOkBKrEAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACJAwAAAAA= " filled="f" stroked="f" strokeweight=".5pt">
| О |
| A |
| x1 |
| x2 |
| • |
| xo1 |
| xo2 |
| Рис. 2.3 |
| А |
| B |
| C |
| D |
|
|
|
Данная целевая функция экономически представляет собой премию за отклонения выпусков x 1и x 2 от заранее заданных их значений x 1°и x 2°, где значения коэффициентов p 1 и p 2определят силу таких премий. Как видим из рис.2.3, при расположении центра эллипсов внутри многогранника условий в точке Е с координатами x 1°и x 2° возможно попадание в локальный оптимум в вершине А. Перемещение из нее в соседние вершины В или D ухудшит значение целевой функции (уменьшит эллипс), хотя в вершине С достигается глобальный оптимум. Итак невыполнение условия 2 ведет и к невыполнению условия 3.
Случай 3. Пусть одно из ограничений будут нелинейным, а именно:
(x 1 - a 1) (x 2 - a 2) £ b 1,
где x 1 и x 2— искомые выпуски двух видов продукции, a 1 и a 2 — минимально разрешенные (по технологическим или экономическим соображениям) размеры производства, a b 1— предельно допустимый уровень загрязнения окружающей среды, мультипликативно зависящий от объемов производства двух видов продукции. Кроме того, имеются обычные ограничения по производственной программе и на неотрицательность переменных
x 1 + x 2³ b 2;
x 1³ 0; x 2³ 0.
На рис. 2.4 заштрихована область допустимых решений. Как
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAbKoCWscA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE7wX/w/IK3uqmEYukriEEQkXsQevF2zP7 TEKzb2N2G2N/fbdQ6HGYmW+YVTqaVgzUu8aygudZBIK4tLrhSsHxo3hagnAeWWNrmRTcyUG6njys MNH2xnsaDr4SAcIuQQW1910ipStrMuhmtiMO3sX2Bn2QfSV1j7cAN62Mo+hFGmw4LNTYUV5T+Xn4 Mgq2efGO+3Nslt9t/ra7ZN31eFooNX0cs1cQnkb/H/5rb7SCeL6A3zPhCMj1DwAAAP//AwBQSwEC LQAUAAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNd LnhtbFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8u cmVsc1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hh cGV4bWwueG1sUEsBAi0AFAAGAAgAAAAhAGyqAlrHAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRy cy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACMAwAAAAA= " filled="f" stroked="f" strokeweight=".5pt">
| О |
| x2 |
| x1 |
| a2 |
| a1 |
Рис.2.4
видим, она состоит из двух несвязанных областей. Более того, каждое из двух подмножеств допустимых решений невыпукло. В этих условиях даже линейность целевой функции не может гарантировать от локального оптимума.
Итак, невыполнение условия 1 ведет к невыполнению условий 3 и 4.
Случай 4. Требование целочисленности решения даже при наличии прочих линейных ограничений и линейной целевой функции ведет к невыполнению условий 1 и 4. Из рис.2.5 видно, что область допустимых целочисленных значений переменных состоит из четырех точек О, А, D и Е, а оптимум достигается в точке D. Причем это решение не только существенно хуже оптимального решения без условий целочисленности (достигается в точке В), но и не может быть получено путем его округления до ближайших целых чисел (точки А и С).
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAn7wQqMcA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPzWrDMBCE74G+g9hCbolcl4bgRjHGYFJCesjPpbet tbFNrZVrKY7Tp68KhRyHmfmGWaWjacVAvWssK3iaRyCIS6sbrhScjsVsCcJ5ZI2tZVJwIwfp+mGy wkTbK+9pOPhKBAi7BBXU3neJlK6syaCb2444eGfbG/RB9pXUPV4D3LQyjqKFNNhwWKixo7ym8utw MQq2efGO+8/YLH/afLM7Z9336eNFqenjmL2C8DT6e/i//aYVxItn+DsTjoBc/wIAAP//AwBQSwEC LQAUAAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNd LnhtbFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8u cmVsc1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hh cGV4bWwueG1sUEsBAi0AFAAGAAgAAAAhAJ+8EKjHAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRy cy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACMAwAAAAA= " filled="f" stroked="f" strokeweight=".5pt">
| О |
| A |
| B |
| C |
| D |
| x2 |
| x1 |
| E |
Рис.2.5
Рассмотренные случаи не являются исчерпывающими и служат лишь иллюстрацией, из которой видно, что в чисто вычислительном аспекте для нелинейных задач характерны затруднения с получением точного решения, либо из-за попадания в локальный оптимум, либо из-за плохой сходимости вычислительного процесса. Кроме того, методы нелинейного программирования в отличие от линейного не являются универсальными и приспособлены для решения лишь ограниченного круга задач того или иного специального класса, а потому гораздо более чувствительны к размерности задач.
С содержательной же стороны использование линейных зависимостей дает возможность предельно прозрачно экономически интерпретировать не только модели, отдельные математические выражения и входящие в них величины, а также результаты решения, но даже и сами вычислительные процедуры. Подобные свойства линейных моделей делают их весьма удобными с методической точки зрения для усвоения в процессе обучения общих экономических принципов и закономерностей.
В экономической практике и исследованиях вычислительная привлекательность и хорошая интерпретируемость линейных моделей (не обязательно оптимизационных, т.е. моделей в широком смысле) делает целесообразным их применение и в случае линейной аппроксимации с приемлемой погрешностью нелинейных закономерностей, если это не мешает экономическому содержанию задачи.
Вопрос 12.
Рассмотрим модель производственной системы (2.7)-(2.9) с точки зрения ценности имеющихся у предприятия ресурсов. Будем иметь в виду, что ресурсы, которые в оптимальном плане не используются полностью, имеют для производственной системы низкую ценность в том смысле, что предприятие не будет согласно нести даже небольшие расходы на увеличение запасов этих ресурсов. Так, дорогое оборудование, не используемое в технологическом процессе, имеет для предприятия нулевую ценность. Наибольшую ценность будут иметь те ресурсы, которые в наибольшей степени ограничивают выпуск продукции, а, следовательно, и доход предприятия, и на увеличение запасов которых предприятие согласно нести значительные расходы.
В связи с этим можно считать, что каждый вид ресурса обладает некоторой “теневой ценой”, определяющей ценность данного ресурса для предприятия с точки зрения дохода от реализации выпускаемой продукции и зависящей от наличного запаса этого ресурса и потребности в нем для выпуска продукции.
Если предприятие ограничивается одним производственным способом, требующим больших затрат некоторого ресурса, запасы которого ограничены, то теневая цена этого ресурса будет велика. Однако установленные в соответствии с этим способом производства теневые цены не будут наилучшими, так как введение других производственных способов позволяет более рационально использовать все запасы ресурсов. Например, если в модели из предыдущего пункта ограничиться способом Р 2, то теневая цена капитала будет очень высокой, а теневая цена труда крайне низкой (при двух единицах капитала его останется 7 единиц). Если же наряду с Р 2 ввести способ производства Р 3 , то теневая цена капитала останется прежней, а теневая цена труда повысится (при двух единицах капитала его останется 2 единицы).
Ясно, что оптимальному состоянию производственной системы в модели (2.7)-(2.9) соответствует вектор оптимальных теневых цен наличного запаса ресурсов. Оптимальные теневые цены называют объективно обусловленными оценками (о.о.о.) или оптимальными оценками, или двойственными оценками ресурсов.
Для определения о.о.о. ресурсов составим самостоятельную задачу линейного программирования.
Обозначим через уi (i =1,2,..., m) о.о.о. i -го ресурса. Величины уi должны быть такими, чтобы сумма теневых цен ресурсов, затрачиваемых при любом используемом производственном способе, не была меньше величины дохода рj :
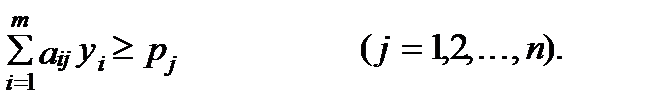
Если производственная система находится в оптимальном состоянии, то ресурсы потребляются в соответствии с их о.о.о., а их суммарная теневая цена является наименьшей возможной
Таким образом, задача определения о.о.о. ресурсов формулируется как следующая оптимизационная задача:
Задача линейного программирования (2.21)-(2.23) называется двойственной задачей по отношению к задаче (2.7)-(2.9). Прямая и двойственная задачи тесно связаны между собой. Эта связь заключается в следующем:
1. если прямая задача является задачей на максимум, то двойственная задача — на минимум;
2. коэффициенты целевой функции в прямой задаче являются свободными членами в ограничениях двойственной задачи и, наоборот, свободные члены из ограничений прямой задачи являются коэффициентами целевой функции двойственной задачи;
3. коэффициенты при переменных в ограничениях двойственной задачи являются столбцами матрицы коэффициентов ограничений прямой задачи;
4. знаки неравенств в системе ограничений прямой задачи меняются на противоположные в системе ограничений двойственной задачи.
Установим связь между решениями прямой и двойственной задач линейного программирования.
Также как и в предыдущем пункте, примем в прямой задаче переменные x 1,..., xn за свободные и сформулируем ее в виде модели (2.11), (2.12), (2.9), обозначив переменные группы ti через переменные xn+ i :
с = 0 -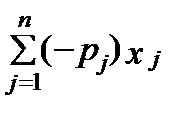 
® max;
xn+ i = bi -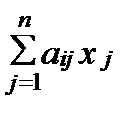 
, xn+ i ³0(i= 1,2,..., m);
хj ³ 0 (j= 1,2,..., n).
Этой задаче соответствует матрица коэффициентов
. (2.24)
В двойственной задаче примем за свободные переменные у 1,..., уm и сформулируем ее в следующем виде:
q = 0 + 
уm+ j = - 
у i ³0; (i =1,2,..., m).
Отметим, что экономическое содержание переменных уm+ j — превышение теневой цены вектора затрат по i -му производственному способу над доходами, выраженными в величине выпуска р j.
Этой задаче соответствует матрица коэффициентов:
. (2.25)
Столбцы матрицы (2.25) являются строками матрицы (2.24), Следовательно, прямая и двойственная задачи описываются одной и той же матрицей, в которой должно быть установлено следующее соответствие между переменными:
(2.26)
Отметим, что любое преобразование матрицы (2.24) по правилам симплекс процедуры приводит к новой матрице, которая описывает новое допустимое (или оптимальное) решение как прямой, так и двойственной задач.
Отсюда следуют важные соотношения, выражающие математические свойства решений прямой и двойственной задач:
1) равенство экстремальных значений целевых функций (верхний левый угол таблиц коэффициентов в последней симплекс-таблице):
2) свободные переменные в оптимальном решении прямой задачи (принимают нулевое значение) соответствуют (в силу 2.26) базисным переменным оптимального решения двойственной задачи (принимают положительные значения) и наоборот. Таким образом, справедливы следующие соотношения “допол-няющей нежесткости”:
(2.28)
Дадим краткую экономическую интерпретацию соотношений (2.27) — первая теорема двойственности и (2.28) — вторая теорема двойственности. Более подробно экономическое содержание двойственных оценок излагается в главе 3.
Итак, соотношение (2.27) показывает, что в оптимальном состоянии суммарный выпуск предприятия совпадает с затратами производственных ресурсов, исчисленными в их теневых ценах. Первое из соотношений (2.28) показывает, что, если i -й производственный ресурс является недефицитным (т.е. выражение в круглых скобках строго положительно), то его теневая цена равна нулю. Наконец, второе из соотношений (2.28) показывает, что если j -й производственный способ является интенсивным, т.е. 
, то величина выпуска р j совпадает с затратами производственных ресурсов по этой технологии.
|
|
|
