 |
Главная задача в методе Данцига-Вульфа. Локальные задачи и экономическая интерпретация метода Данцига-Вульфа.
|
|
|
|
Для записи модели главной задачи введем следующие обозначения:
– индекс (номер) базисного плана t – ого предприятия ( = 1,2,…, 
)
- вектор выпуска продукции t – ого предприятия по базисному плану (размерностью 
×1)
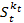- вектор расхода общих ресурсов на весь выпуск (размерностью m×1)
- весь объем прибыли от выпуска
- удельный вес (доля), с которой базисный план предприятия t войдет в план объединения в главной задаче.
Вектор выпуска продукции предприятием t есть линейная комбинация
= 
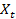Модель главной задачи:
≤ 
= 1 (t=1,2,…,T)
≥ 0 (t = 1,2,…,T; = 1,2,…, )
→ max.
Где, t – индекс предприятия, входящего в отрасль, - вектор лимитов общих ресурсов.
Главная задача эквивалентна исходной задаче. Условия описывают расход общих ресурсов на реализацию планов выпуска. В ограничениях = 1 (t=1,2,…,T) единица в правых частях олицетворяет производственную мощность предприятия, а сумма долей слева показывает, в какой пропорции эта производственная мощность делится между отдельными базисными планами, «смесь» которых формирует план данного предприятия. «Смесь» допустимых базисных планов в пределах производственной мощности предприятия даст допустимый план. Из неотрицательности долей по формуле 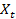= следует неотрицательность 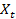. → max означает максимизацию прибыли объединения как суммы прибыли по отдельным предприятиям.
Модель локальной задачи предприятия t:
≤ 
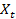≥ 0
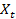) → max
Где, 
- матрица коэфф. (норм) затрат локальных ресурсов на выпуск продукции предприятием t, 
- вектор удельной прибыли от выпуска продукции предприятием t,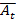 
- матрица коэфф. (норм) затрат общих ресурсов на выпуск продукции предприятием t, V – вектор оценок общих ресурсов.
|
|
|
Критерием оптимальности в локальной задаче является максимум «чистой» прибыли предприятия t, т.е. прибыли от его деятельности за вычетом затрат на использованные общие ресурсы, исчисленные в оценках главной задачи.
На каждой итерации предприятия стремятся улучшить свой план, учитывая локальные условия и «цены» на общие ресурсы, т.е. найти такой его вариант, который дал бы максимум прибыли в предложенных ценах. Определив улучшенные варианты плана, предприятия сообщают их наверх.
На новой итерации объединение пересчитывает главную задачу, вводя в нее новый вариант плана, у которого прибыль превзошла предполагаемую ранее. На уровне объединения получаются скорректированные оценки, соответствующие новому плану объединения. И так до получения сбалансированного во всех звеньях оптимального плана всего объединения.
Объединение определяет и корректирует план нижестоящих объектов, чем и определяется координация решений, принимаемых предприятиями. Оптимальный план объединения формируется как совокупность частных оптимумов, направленных на выполнение единой цели.
План системы в целом последовательно улучшается путем взаимного уточнения планов отдельных предприятий. В схеме реализуется фундаментальное положение теории оптимального планирования: план, цены и показатели стимулирования хозяйственной деятельности должны быть взаимоувязаны и получаться из единого решения производственной задачи на оптимум. На стадии планирования закладываются экономические условия для выполнения оптимального плана, а так же стимулиркется выявление новых производственных возможностей.
24. Методы многоуровневой оптимизации: Центральная задача в методе Корнаи-Липтака. Экономическое содержание двойственных оценок в этой задаче.
В этом методе итерактивный процесс двухступенчатой оптимизации планов развития объединения и отдельных предприятий основан не на корректировке двойственных оценок ресурсов и продукции, а на корректировке выделяемых предприятиям лимитов ресурсов и заданий по выпуку продукции в натуральном выражении в соответствии с анализом и сравнением предельных эффективностей (оценок) их использования на предприятиях.
|
|
|
Проведем посекторное (по предприятиям) разбиение векторов лимитов общих ресурсов.
+ … + 
+ … + 
= ,
Где, - вектор лимитов общих ресурсов, выделяемых объединению предприятию.
Получаем для первого шага секторные задачи, их планы, значения прибыли и секторные оценки общих ресурсов 
.
Наша цель – найти такое распределение ресурсов, при котором сумма секторных функционалов будет равна истинному оптимуму. Для этого достаточно, что бы двойственные оценки одноименного общего ресурса в различных секторах были равны между собой
= 
= … = = … = 
= 
.
Оценка показывает приращение критерия оптимальности (прибыли) t-й секторной задачи при увеличении количества i-ого общего ресурса, выделяемого данному сектору, на 1 ед. Секторные оценки общих ресурсов характеризуют эффективность их распределения между предприятиями.
Для нахождения нового варианта распределения ресурсов на верхнем уровне (в объединении) строится центральная задача. В ней ищутся вектора 
, ограничением является вектор . Цель – максимизировать эффект от перераспределения ресурсов объединения, исчисленный в секторных оценках предыдущего шага. Модель центральной задачи:
≤ ;
≥ 0; (t =1,2,…, T)
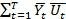→ max,
Где,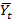 
- вектор оценок ресурсов объединения в t-секторе.
В силу неравенства оценок одного и того же общего ресурса в разных секторах, в центральной задаче весь объем данного ресурса распределится в тот сектор, где оценка наибольшая. Такое радикальное распределение ресурсов будет повторяться на каждом шаге. Для обеспечения сходимости итерактивного процесса вниз, в сектора (на редприятия) сообщается скорректированное перераспределение ресурсов, т.е. вектора 
Где, µ - номер предыдущей итерации; (µ+1) – нескорректированное решение центральной задачи на данном шаге; 
и 
- скорректированные решения центральной задачи данного и предыдущего шагов соответственно.
|
|
|
Это означает, что предприятию с максимальной оценкой общего ресурса, количество этого ресурса увеличивается, а для всех остальных – уменьшается, причем таким образом, чтобы в сумме не выйти за пределы лимита ресурсов объединения 
|
|
|
