 |
Вопрос 27. Понятие производственной функции. Проблемы и особенности её моделирования.
|
|
|
|
Поскольку каждая производственная изокванта  характеризуется величиной выпуска
характеризуется величиной выпуска  , то возникающее соотношение
, то возникающее соотношение

называется производственной функцией (ПФ) предприятия, а точнее его частичной производственной функцией (ЧПФ), определенной в конкретной (-ых) точке (-ах) его экономической области Ω.
Опр.. Функция  где
где  – подмножество экономической области Ω, включающее наборы факторов производства, принадлежащих производственной изокванте
– подмножество экономической области Ω, включающее наборы факторов производства, принадлежащих производственной изокванте  , называется частичной производственной функцией.
, называется частичной производственной функцией.
Если соотношение (1) установлено для всех допустимых наборов  производственных факторов предприятия из экономической области Ω, то соответствующая ему ПФ является полной (ППФ), определенной на всей верхней полурешетке
производственных факторов предприятия из экономической области Ω, то соответствующая ему ПФ является полной (ППФ), определенной на всей верхней полурешетке  .
.
Опр.. Функция  где
где  – верхняя полурешетка, включающая все допустимые изокванты
– верхняя полурешетка, включающая все допустимые изокванты  называется полной производственной функцией.
называется полной производственной функцией.
ППФ задается выражением 
ППФ выбирается так, что она наилучшим в смысле отношения ρ образом приближает (аппроксимирует) ЧПФ  в узлах верхней полурешетки
в узлах верхней полурешетки  .
.
В качестве возможных отношений (мер отличия) ρ, как правило, используются следующие метрики:
1) равномерное приближение:


2) среднеквадратическое приближение (Евклидово расстояние):

Для выбранной ППФ f расстояние в смысле метрики  должно принимать наименьшее значение.
должно принимать наименьшее значение.
Особенностью моделирования ППФ является то, что в зависимости от выбора способа аппроксимации (ρ) зависит ее степень гладкости. Как известно, это свойство ППФ является определяющим для дальнейшего ее анализа и построения моделей.
В связи с этим можно выделить следующие проблемы моделирования ППФ:
1) Большая сложность вычисления ППФ
|
|
|
2) Полученная ППФ не обладает нужной степенью гладкости
Вопрос 28. Производственная функция и экономическая область предприятия. Моделирование частичной и полной производственной функции (на основе численных методов).
Экономическая область предприятия, которую иначе называют областью производственных возможностей, включает все допустимые наборы производственных факторов  , которые могут быть приобретены предприятием с использованием оборотного капитала величиной M.
, которые могут быть приобретены предприятием с использованием оборотного капитала величиной M.
Опр.. Экономическая область предприятия задается множеством векторов  факторов производства в пространстве
факторов производства в пространстве 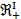 :
:

Поскольку каждая производственная изокванта  характеризуется величиной выпуска
характеризуется величиной выпуска  , то возникающее соотношение
, то возникающее соотношение

называется производственной функцией (ПФ) предприятия, а точнее его частичной производственной функцией (ЧПФ), определенной в конкретной (-ых) точке (-ах) его экономической области Ω.
Опр.. Функция  где
где  – подмножество экономической области Ω, включающее наборы факторов производства, принадлежащих производственной изокванте
– подмножество экономической области Ω, включающее наборы факторов производства, принадлежащих производственной изокванте  , называется частичной производственной функцией.
, называется частичной производственной функцией.
Если соотношение (1) установлено для всех допустимых наборов  производственных факторов предприятия из экономической области Ω, то соответствующая ему ПФ является полной (ППФ), определенной на всей верхней полурешетке
производственных факторов предприятия из экономической области Ω, то соответствующая ему ПФ является полной (ППФ), определенной на всей верхней полурешетке  .
.
Опр.. Функция  где
где  – верхняя полурешетка, включающая все допустимые изокванты
– верхняя полурешетка, включающая все допустимые изокванты  называется полной производственной функцией.
называется полной производственной функцией.
ППФ задается выражением 
Отметим отличия ППФ и ЧПФ.
Во-первых, ППФ  определена на всей верхней полурешетке
определена на всей верхней полурешетке  , а не только на выделенных изоквантах
, а не только на выделенных изоквантах  , как ЧПФ
, как ЧПФ  . Во-вторых, ППФ
. Во-вторых, ППФ  , обладая заданными аналитическими свойствами, отличается качеством приближения ЧПФ
, обладая заданными аналитическими свойствами, отличается качеством приближения ЧПФ 
Предполагается, что ППФ  обладает свойством гладкости в смысле принадлежности к классу
обладает свойством гладкости в смысле принадлежности к классу  (где k – степень гладкости функции) непрерывно дифференцируемых на множестве Ω функций.
(где k – степень гладкости функции) непрерывно дифференцируемых на множестве Ω функций.
|
|
|
Резюмируя изложенное, приведем основные этапы моделирования ППФ:
1. Определяем экономическую область предприятия – верхнюю полурешетку  ;
;
2. В узлах решетки  решаем задачу определения наибольшего (в стоимостном выражении) объема выпуска, что позволяет в табличной форме построить ЧПФ
решаем задачу определения наибольшего (в стоимостном выражении) объема выпуска, что позволяет в табличной форме построить ЧПФ  ;
;
3. Определяем принадлежность ППФ к определенному классу  и выбираем метрику
и выбираем метрику  ;
;
4. Оцениваем качество приближения. Возвращаемся к пункту 3, либо делаем вывод об удовлетворительности полученного образа ППФ f.
Вопрос 29. Характеристики производственной функции нулевого и первого порядков и их экономическая интерпретация.
Количественными характеристиками ПФ  нулевого порядка являются следующие:
нулевого порядка являются следующие:
1) полная производительность  - го производственного фактора в окрестности точки
- го производственного фактора в окрестности точки  :
:

где  - фиксированные объемы производственных факторов (кроме i - го) в точке
- фиксированные объемы производственных факторов (кроме i - го) в точке  .
.
Показатель характеризует величину выпуска, обусловленную затратами  - го фактора, при фиксированных затратах факторов
- го фактора, при фиксированных затратах факторов  .
.
2) средняя отдача (производительность)  - го производственного фактора (average product) в точке
- го производственного фактора (average product) в точке  :
:

Средняя отдача  - го производственного фактора характеризует величину выпуска, приходящегося на ед. затрачиваемого
- го производственного фактора характеризует величину выпуска, приходящегося на ед. затрачиваемого  - го фактора.
- го фактора.
1) совокупная рентабельность активов в точке  :
:

Совокупная рентабельность характеризует величину выпуска, приходящуюся на ед. обобщенного ресурса.
2) норма отдачи единицы  -го производственного фактора (в стоимостном выражении) в точке
-го производственного фактора (в стоимостном выражении) в точке  :
:

3) норма отдачи ед. производственного капитала предприятия в точке  :
:

где  - полная стоимость используемых в процессе производства факторов (величина привлекаемого производственного капитала).
- полная стоимость используемых в процессе производства факторов (величина привлекаемого производственного капитала).
Норма отдачи характеризует рентабельность производственного капитала предприятия.
4) доход в точке  :
:


Показатель характеризует экономический эффект: разница между достигнутым экономическим результатом производства и затратами на его достижение.
Количественными характеристиками ПФ  первого порядка являются следующие:
первого порядка являются следующие:
1) предельная (маржинальная) отдача (предельный выпуск) (marginal product) i-го производственного фактора в точке  :
:
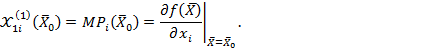
Предельная отдача  -го производственного фактора в случае положительного эффекта масштаба производства
-го производственного фактора в случае положительного эффекта масштаба производства  характеризует прирост объема выпуска по
характеризует прирост объема выпуска по  - му фактору (в стоимостном выражении) при увеличении производственного потребления этого фактора на одну ед. и при неизменных объемах затрат остальных факторов.
- му фактору (в стоимостном выражении) при увеличении производственного потребления этого фактора на одну ед. и при неизменных объемах затрат остальных факторов.
|
|
|
2) эластичность выпуска (elasticity) по i - му производственному фактору в точке  :
:

Показатель эластичности характеризует процентное[2] изменение выпуска, связанное с изменением потребления  -го производственного фактора на один процент. Рост производства имеет место быть, если
-го производственного фактора на один процент. Рост производства имеет место быть, если  , в противном случае – падение
, в противном случае – падение  . Такая ситуация возможна в случае, если финансирование производственного фактора требует больших затрат, чем отдача от его использования.
. Такая ситуация возможна в случае, если финансирование производственного фактора требует больших затрат, чем отдача от его использования.
3) суммарная эластичность по всем производственным факторам в точке  :
:

Показатель суммарной эластичности характеризует соотношение относительных приростов выпуска и затрат при пропорциональном изменении последних.
Вопрос 30. Неоклассические производственные функции, их свойства. Однородные производственные функции. Масштаб производства и его связь со степенью однородности.
Итак, будем далее полагать, что ППФ определена на всей верхней полурешетке  , принадлежит классу
, принадлежит классу  и удовлетворяет следующим условиям:
и удовлетворяет следующим условиям:
1)  в экономической области Ω монотонно неубывающая по каждому аргументу (рис. 1.2):
в экономической области Ω монотонно неубывающая по каждому аргументу (рис. 1.2):

Указанное свойство следует из характера построения верхней полурешетки  .
.
2) по каждому аргументу  выпукла вверх (вогнута):
выпукла вверх (вогнута):

Это условие по существу является следствием закона убывающей предельной отдачи производственного фактора: с ростом затрат i - го фактора при постоянных затратах остальных факторов производства предельная отдача данного фактора падает.
3)  экономически непротиворечива, т.е.
экономически непротиворечива, т.е.  что означает факт отсутствия выпуска при нулевых затратах производственных факторов.
что означает факт отсутствия выпуска при нулевых затратах производственных факторов.
Данное свойство ПФ  напрямую вытекает из свойства замкнутости верхней полурешетки
напрямую вытекает из свойства замкнутости верхней полурешетки  , согласно которому нулевой вектор
, согласно которому нулевой вектор  затрат производственных факторов соответствует нулевой изокванте.
затрат производственных факторов соответствует нулевой изокванте.
|
|
|
4) ПФ однородна по всей совокупности аргументов, т.е. если существует константа  , называемая показателем эффективности производства или степенью однородности производственной функции, такая, что для
, называемая показателем эффективности производства или степенью однородности производственной функции, такая, что для  ,
,  и любого масштаба производства
и любого масштаба производства  такого, что новый набор
такого, что новый набор  , справедливо равенство:
, справедливо равенство:

5) наличие взаимозаменяемости двух или более производственных факторов, позволяющей гарантировать постоянство выпуска путем замещения одного фактора другим.
В случае неполной взаимозаменяемости факторов предполагается наличие неуменьшаемого остатка одного фактора при условии возможности замещения необходимого объема этого фактора соответствующим объемом другого фактора.
Опр.. ПФ  , удовлетворяющая условиям 1) - 5), называется неоклассической ПФ.
, удовлетворяющая условиям 1) - 5), называется неоклассической ПФ.
Вопрос 31. Неоклассические изокванты и их свойства. Графическое решение задач замены производственных факторов и выбора оптимального набора факторов
Опр.. Производственной изоквантой  уровня
уровня  для заданной технологии
для заданной технологии  называется множество векторов
называется множество векторов  , которым соответствует одна и та же стоимостная оценка результата
, которым соответствует одна и та же стоимостная оценка результата 
 :
:

Опр.. Частично упорядоченное множество  , все двухэлементные подмножества которого имеют точную верхнюю грань, принадлежащую Ω, называется верхней полурешеткой и обозначается
, все двухэлементные подмножества которого имеют точную верхнюю грань, принадлежащую Ω, называется верхней полурешеткой и обозначается  .
.
Основываясь на этом определении можно утверждать, что наборы производственных изоквант  структурируют экономическую область
структурируют экономическую область  в виде верхней полурешетки
в виде верхней полурешетки  .
.
Отметим, что верхняя полурешётка производственных изоквант  обладает следующими вполне очевидными свойствами:
обладает следующими вполне очевидными свойствами:
1) замкнутость. Верхняя полурешетка  содержит как наименьший 0, так и наибольший I элементы, первому из которых соответствует изокванта
содержит как наименьший 0, так и наибольший I элементы, первому из которых соответствует изокванта  нулевого выпуска
нулевого выпуска  , второму – изокванта
, второму – изокванта  максимального выпуска среди всех допустимых наборов
максимального выпуска среди всех допустимых наборов  ;
;
2) рефлексивность. Согласно условию (1.4) и определению 1.6 два набора  являются неразличимыми, если они принадлежат одной производственной изокванте
являются неразличимыми, если они принадлежат одной производственной изокванте  :
: 
3) антисимметричность. Из условия (1.5) следует, что любые наборы  ,такие, что
,такие, что  и
и  , неразличимы, а, следовательно, принадлежат одной изокванте;
, неразличимы, а, следовательно, принадлежат одной изокванте;
4) транзитивность. В силу условия (1.6), если  ,
,  ,
,  , то, во-первых,
, то, во-первых,  , а во-вторых,
, а во-вторых, 
5) выпуклость. Если  – допустимые наборы факторов производства, связанные условием
– допустимые наборы факторов производства, связанные условием  , то для
, то для  справедливо:
справедливо:  .
.
Экономическую область Ω можно представить в виде упорядоченного набора производственных изоквант, называемого картой изоквант (рис. 1.5), демонстрирующей следующие особенности взаимозаменяемости производственных факторов  :
:
- изокванта  , лежащая выше и правее некоторой
, лежащая выше и правее некоторой  , соответствует большему объему выпуска:
, соответствует большему объему выпуска:  ;
;
|
|
|
- изокванты имеют отрицательный наклон;
- изокванты, соответствующие разным уровням производства, не пересекаются.
На рис. 1.6 представлена карта производственных изоквант для случая двухфакторного производственного процесса. Все точки изокванты, расположенные вне дуги  , представляют неэффективные варианты производства продукции. Так, точка
, представляют неэффективные варианты производства продукции. Так, точка  соответствует варианту производства с использованием
соответствует варианту производства с использованием  единиц фактора
единиц фактора  и
и  единиц фактора
единиц фактора  . Аналогичный объем производства (в стоимостном выражении) с такими же затратами фактора
. Аналогичный объем производства (в стоимостном выражении) с такими же затратами фактора  можно произвести, применяя лишь
можно произвести, применяя лишь  единиц второго фактора.
единиц второго фактора.

|

|

|

|

|

|

|

|

|
| D |
| C |
| B |
| A |
Рис. 1.6. Эффективные и неэффективные области изокванты для случая двухфакторной производственной функции.
- абсолютное значение наклона изокванты при ее движении вправо уменьшается, и она становится более пологой. Отдельно поясним, что расположение изокванты относительно осей координат определяется соотношением эластичностей выпуска по факторам производства (рис. 1.7). Если  , то изоквантасимметрична биссектрисе первого координатного угла (II). При
, то изоквантасимметрична биссектрисе первого координатного угла (II). При  изокванта имеет относительно больший наклон к оси
изокванта имеет относительно больший наклон к оси  (III), а при
(III), а при  — наоборот (I).
— наоборот (I).
Вопрос 32. Нелинейные модели производства: Двойственная оценка производственного фактора. Норма замены факторов, эластичность замены и ее связь с двойственными оценками.
Отметим, что в рамках одной производственной изокванты предельная отдача ресурса совпадает с его двойственной оценкой.
Таким образом, в задачах моделирования производства следует учитывать 1-ое, 2-ое и 4-ое свойства двойственных оценок ресурсов, которые количественно оценивают эффективность рыночной стратегии предприятия в сфере производственных факторов.
Напомним упомянутые свойства.
По первому свойству «двойственная оценка - мера дефицитности ресурсов».
По второму свойству «двойственная оценка - мера влияния ограничения на функционал модели».
По четвертому свойству «оценка - инструмент балансирования затрат и результатов». Данное свойство можно продемонстрировать следующим выражением:
Согласно определению, производственная изокванта 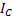 является кривой постоянного выпуска
является кривой постоянного выпуска  .
.
Поскольку изокванта - кривая постоянного выпуска, то его приращение вдоль изокванты равно нулю, т.е.  .Кроме того, ППФ
.Кроме того, ППФ  в силу первой предпосылки является дифференцируемой в любой точке экономической области предприятия Ω, а ее дифференциал
в силу первой предпосылки является дифференцируемой в любой точке экономической области предприятия Ω, а ее дифференциал  в точке
в точке  может быть представлен в виде:
может быть представлен в виде:

Откуда

где  - предельная норма замены второго фактора первым.
- предельная норма замены второго фактора первым.
Предельная норма замены  характеризует абсолютный объем увеличения затрат первого ресурса при условии сохранения объема выпуска
характеризует абсолютный объем увеличения затрат первого ресурса при условии сохранения объема выпуска  в случае, если затраты второго ресурса снизятся на одну ед. Таким образом, норма замены производственных факторов, обратно пропорциональна их предельным производительностям.
в случае, если затраты второго ресурса снизятся на одну ед. Таким образом, норма замены производственных факторов, обратно пропорциональна их предельным производительностям.
Воспользовавшись определением эластичности, соотношение (1) можно переписать в следующем виде:

Полученное соотношение позволяет получить выражение для показателя эластичности замещения второго производственного фактора первым:

Эластичность  замещения второго фактора первым при фиксированном объеме выпуска
замещения второго фактора первым при фиксированном объеме выпуска  характеризует процентное изменение объема потребления первого фактора при изменении объема потребления второго фактора на один процент.
характеризует процентное изменение объема потребления первого фактора при изменении объема потребления второго фактора на один процент.
Вопрос 33. Вывод и обоснование экономического содержания множителя Лагранжа для неоклассической производственной функции
В предложенных терминах экономико-математическая модель минимизации производственных издержек (стоимости производственного капитала) предприятия принимает следующий вид:

 ; (2)
; (2)

где  - рыночная стоимость используемого набора
- рыночная стоимость используемого набора  производственных факторов;
производственных факторов;  - ППФ предприятия;
- ППФ предприятия;  - заданный объем выпуска в стоимостном выражении.
- заданный объем выпуска в стоимостном выражении.
Нетрудно показать, что неравенство (2) можно заменить равенством. В этом случае модель минимизации издержек примет вид:

 ; (5)
; (5)

Функция Лагранжа для отыскания условного экстремума в данном случае имеет вид:  Условием оптимальности найденного решения является равенство нулю всех первых частных производных функции Лагранжа, откуда получим следующую систему условий оптимальности:
Условием оптимальности найденного решения является равенство нулю всех первых частных производных функции Лагранжа, откуда получим следующую систему условий оптимальности:


где: 

Преобразуем выражение (7) к следующему виду:

показывающему, что стоимость фактора, приходящаяся на одну ед. его предельной отдачи для любого производственного фактора является величиной постоянной.
Построим функцию производственных издержек, связывающую издержки производства  с объемом выпускаемой продукции:
с объемом выпускаемой продукции:

которая, очевидно, также принадлежит классу  , а, следовательно, ее можно дифференцировать и на этой основе определить количественные характеристики нулевого и первого порядков, к которым относятся средние и предельные издержки, а также показатель эластичности издержек по выпуску.
, а, следовательно, ее можно дифференцировать и на этой основе определить количественные характеристики нулевого и первого порядков, к которым относятся средние и предельные издержки, а также показатель эластичности издержек по выпуску.
Функция производственных издержек в силу соотношения (7) принимает следующий вид:

т.к. 
Умножим правую часть выражения на  , полагая, что оптимальный набор
, полагая, что оптимальный набор  не принадлежит нулевой изокванте
не принадлежит нулевой изокванте  , т.е.
, т.е.  . Получим:
. Получим:


С учетом определения суммарной эластичности в точке  функция
функция
 производственных издержек может быть представлена следующим образом:
производственных издержек может быть представлена следующим образом:

или с учетом условия оптимальности:

Выражение для функции производственных издержек позволяет определить ее основные количественные характеристики, например, предельные издержки производства в точке  :
:

Докажем справедливость этого соотношения. Найдем значение дифференциала 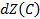 в точке
в точке  :
:


ППФ  в силу ее принадлежности классу
в силу ее принадлежности классу  дифференцируема в любой точке
дифференцируема в любой точке  . Значение дифференциала
. Значение дифференциала  в точке
в точке  принимает следующий вид:
принимает следующий вид:

Откуда получаем:  , что и требовалось доказать.
, что и требовалось доказать.
Полученное соотношение позволяет интерпретировать множитель Лагранжа  для задачи минимизации совокупных издержек как предельные издержки
для задачи минимизации совокупных издержек как предельные издержки  для заданного объема выпуска
для заданного объема выпуска  .
.
Вопрос 34. Моделирование производственных издержек. Спрос на факторы производства. Основные соотношения теории предельной полезности производственных факторов.
С учетом допущения о том, что ПФ  является неубывающей в технологической области предприятия (области возможных наборов ПФ), а её полный образ для каждого объема выпуска
является неубывающей в технологической области предприятия (области возможных наборов ПФ), а её полный образ для каждого объема выпуска  аппроксимируется гладкой изоквантой (достаточно первого порядка гладкости), сформулируем задачу минимизации производственных издержек предприятия, основной целью построения которой является определение на заданной производственной изокванте
аппроксимируется гладкой изоквантой (достаточно первого порядка гладкости), сформулируем задачу минимизации производственных издержек предприятия, основной целью построения которой является определение на заданной производственной изокванте 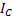 уровня
уровня  в условиях полной взаимозаменяемости производственных факторов набора факторов
в условиях полной взаимозаменяемости производственных факторов набора факторов  минимальной рыночной стоимости
минимальной рыночной стоимости 
 .
.
В предложенных терминах экономико-математическая модель минимизации производственных издержек (стоимости производственного капитала) предприятия принимает следующий вид:

 ; (2)
; (2)

где  - рыночная стоимость используемого набора
- рыночная стоимость используемого набора  производственных факторов;
производственных факторов;  - ППФ предприятия;
- ППФ предприятия;  - заданный объем выпуска в стоимостном выражении.
- заданный объем выпуска в стоимостном выражении.
Воспользуемся условиями теоремы Куна-Таккера применительно к задаче (1)-(3) на условный экстремум с ограничениями в виде неравенств и составим для нее функцию Лагранжа, которая в данном случае имеет вид:

Поскольку решается задача на минимум, то целевая функция и множество допустимых решений задачи (1)-(3) должны быть выпуклы.
Т. к.  - линейная функция, то условие выпуклости целевой функции выполняется автоматически. ППФ
- линейная функция, то условие выпуклости целевой функции выполняется автоматически. ППФ  - строго вогнутая по каждому аргументу на множестве Ω функция, а, следовательно, «-
- строго вогнутая по каждому аргументу на множестве Ω функция, а, следовательно, «-  » - выпуклая функция.
» - выпуклая функция.
Таким образом, множество Ω удовлетворяет условию Слейтера, что позволяет применить условия теоремы Куна-Таккера к модели (1)-(3):






где  - решение задачи (1)-(3).
- решение задачи (1)-(3).
Из условий оптимальности следует, что  в случае, если
в случае, если  .
.
Т. к. все  , то
, то  для всех
для всех  .
.
Откуда следует, что 
 для всех
для всех  .
.
Наконец, поскольку  , то получаем, что
, то получаем, что  .
.
Принимая во внимание полученное равенство, можем заключить, что задача (1)-(3) эквивалентна следующей задаче на минимум:



В точке  оптимального по критерию минимума совокупных производственных издержек набора производственных факторов, как следует из условий оптимальности, предельные отдачи
оптимального по критерию минимума совокупных производственных издержек набора производственных факторов, как следует из условий оптимальности, предельные отдачи  факторов прямо пропорциональны их рыночным ценам
факторов прямо пропорциональны их рыночным ценам  .
.
Опираясь на определение предельной нормы замены производственных факторов, получим следующее его обобщение, составляющее основу неоклассической теории предельной полезности факторов производства:

которое указывает на то, что в точке оптимума  предельные производительности факторов прямо пропорциональны, а предельная норма их замены - обратно пропорциональна их рыночным ценам.
предельные производительности факторов прямо пропорциональны, а предельная норма их замены - обратно пропорциональна их рыночным ценам.
Так как заданному объему выпуска  в экономической области Ω соответствует только одна производственная изокванта
в экономической области Ω соответствует только одна производственная изокванта  , то можно сделать вывод о том, что решение задачи минимизации совокупных издержек для каждого уровня производства
, то можно сделать вывод о том, что решение задачи минимизации совокупных издержек для каждого уровня производства  является единственным:
является единственным:

и задает зависимость между объемом производства  и минимальным по стоимости набором производственных факторов
и минимальным по стоимости набором производственных факторов  , т.е., иными словами, задает спрос на производственные факторы.
, т.е., иными словами, задает спрос на производственные факторы.
Вопрос 35. Моделирование функции прибыли. Оптимальный размер предприятия и его аналитическое выражение для случая неоклассической производственной функции.
В долгосрочном периоде, когда есть время изменить любые ресурсы, предприятие стремится найти свой оптимальный размер для производства данного количества продукции при минимальных издержках. Таким образом, поведение издержек в долгосрочном периоде есть главный фактор, определяющий количество и размеры предприятий отрасли.
Критерием эффективности деятельности предприятия является его доход, задаваемый функцией прибыли:

где  - цена реализации ед. продукции;
- цена реализации ед. продукции;  - объем выпуска;
- объем выпуска;  - производственные издержки.
- производственные издержки.
Предполагается, что объем  выпускаемой продукции описывается ПФ
выпускаемой продукции описывается ПФ  .
.
Задача максимизации прибыли принимает следующий вид:



Запишем необходимое условие экстремума для функции прибыли:


