Локальность свойств двойственных оценок ресурсов и технологий. Определение интервала устойчивости двойственных оценок по ресурсам.

Границы устойчивости оценок зависят от устойчивости не величин, а номеров базисных переменных оптимального плана. Определяются границы устойчивости выходом хотя бы одной переменной из базиса, т.е. ее уменьшением до нуля.

При каких условиях в оптимальном плане переменные будут менять свою величину?

=

где dji - элементы матрицы D. Изменим величины ресурсов, дав им приращение ∆bi. Тогда изменятся и значения неизвестных:

+ ∆ = = +

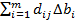
Очевидно, что

∆ =

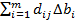
Для простоты положим, что меняется значение лишь одного k -го ресурса, т.е. ∆ ≠ 0, а ∆b_i= 0 для всех i ≠ k. Тогда ∆ =

Для нахождения границ устойчивости оценок нас интересуют лишь случаи уменьшения величины базисных переменных оптимального плана , причем уменьшения до нуля, т.е. ∆ = - .

Итак, выход на границы устойчивости оценок имеет место в случае

- =

Легко определить требуемое для этого значение изменения ресурсов. При положительном коэффициенте 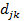требуется уменьшать k-й ресурс, при отрицательном коэффициенте 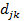— увеличивать. Так как изменение k-го ресурса будет изменять все базисные переменные , то граница устойчивости определится самым чувствительным из них, т.е. тем, который быстрее прочих уменьшится до нуля. Достаточно выхода из базиса лишь одного переменного и появления на его месте нового с новым номером, чтобы изменить оценки. Поэтому требуемое для достижения границ устойчивости увеличение k-го ресурса определится из выражения

∆ = > 0, для ;

а уменьшение — из выражения

∆ = , для > 0.

Естественно, что при = 0 изменение k-го ресурса, не способно изменить величину . Изменим сразу все (несколько) лимитов ресурсов в фиксированной пропорции (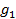, ,..., , ). Изменения каждого i-го ресурса и всего вектора ограничений в целом ∆b свяжет выражение = 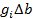, c учетом которого условие преобразуется так

-

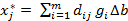
В свою очередь, аналогично получим:

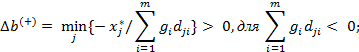
22. Методы многоуровневой оптимизации: метод декомпозиции Данцига-Вульфа. Двойственные оценки и их экономическое содержание.

Метод разложения (декомпозиции) Данцига – Вулфа был разработан для решения задач линейного программирования большой размерности, имеющих блочную структуру. Детальное моделирование процесса выпуска продукции и расходования ресурсов исходной задачи требует включения в модель объединения описания предприятий. Это ведет к большой размерности задачи на уровне объединения и трудностей при ее решении. Метод Данцига-Вулфа предусматривает разложение исходной задачи на локальные задачи, соответствующие обособленным частям объединения, и главную задачу (объединение в целом) и связывает эти задачи.

На каждом шаге процесса решения выполним следующие операции: а) получим решение б) проверим полученный план на оптимальность в) в случае неоптимальности выявим тот вектор, который нужно ввести в базис (опорный план) улучшенного плана. В методе Данцига-Вулфа этот процесс распределяется между главной и локальными задачами.

После получения решения на уровне объединения в главной задаче (этап а) следует обращение к локальным задачам. Путем решения каждой локальной задачи мы должны проверить на оптимальность полученное решение главной задачи (этап б) и, если оно не оптимально, найти тот вариант плана какого-либо из предприятий, который надо ввести в базис главной задачи, что бы улучшить план объединения (этап в).

Введем обозначения:

V – вектор оценок общих ресурсов, каждая из которых показывает, сколько условных единиц прибыли приносит 1 единица соответствующего общего ресурса в плане объединения.

– совокупная оценка t - ого предприятия, которая показывает, сколько условных единиц прибыли приносит предприятие t.

Эти оценки доводятся до сведения отдельных предприятий, которые на их основе и, учитывая собственные ресурсы, ищут новые варианты плана.