 |
При внезапном изменении внешнего момента
|
|
|
|
При установившемся режиме работы положение ротора СМ относительно поля определяется углом 
. В первом приближении этот угол можно считать равным углу между векторами ЭДС возбуждения 
и напряжением 
.
Допустим, что неявнополюсная СМ работает в режиме генератора параллельно с мощной сетью. При этом внешний момент 
(момент первичного двигателя) уравновешивается электромагнитным тормозным моментом машины 
, т. е. 
. На угловой характеристике этому режиму соответствует точка 1 и угол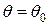 
(рис. 3.47,а).
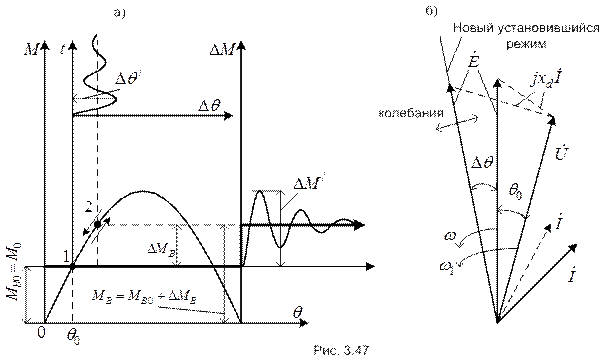
Пусть в момент времени 
внешний момент скачкообразно изменяется до величины 
. В результате возникает избыточный вращающийся момент 
под действием которого, скорость ротора будет расти с ускорением
,
где J – момент инерции ротора;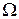 
– угловая скорость ротора.
Это увеличение скорости и нарастание угла 
будет происходить до тех пор, пока внешний момент преобладает над моментом генератора. Равновесие этих моментов наступает в точке 2, в которой . Однако при этом режим не устанавливается, и скорость продолжает расти с отрицательным ускорением за счет запасенной кинетической энергии ротора. При некотором значении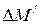 
увеличение угла нагрузки достигает максимального значения 
, после чего скорость ротора начинает уменьшаться, причем будет уменьшаться и угол нагрузки и т.д. Колебания ротора будут продолжаться до тех пор, пока машина не займет нового устойчивого положения, определяемого точкой 2.
Колебания угла равносильны колебаниям вектора (рис. 3.47, б).
Для математического описания движения ротора, при колебаниях, удобно выразить момент В зависимости от начального угол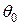 
и его приращения 
. С этой целью через эти величины выразим следующие параметры.
|
|
|
1. Электрическая угловая скорость ротора в предположении однополупериодной модели 
.
2. Угловная скорость ротора 
.
3. Скольжение ротора 
.
4. Угловое ускорение ротора 
.
5. Синхронный электромагнитный момент, действующий на ротор, при угле будет 
,
где 
- коэффициент синхронизирующего момента.
В случае неявнополюсной СМ имеем
, 
.
6. Асинхронный электромагнитный момент взаимодействия токов, индуктированных в демпферной обмотке и обмотке возбуждения с результирующем полем.
При малых скольжениях этот момент можно записать следующим образом
,
где 
– коэффициент демпфирования.
За положительное направления синхронного момента будем считать направление в сторону вращения ротора.
Таким образом, уравнение движения ротора СМ после внезапного изменения внешнего момента можно записать в виде
,
или 
и
.
Преобразуя данное уравнение, получим линейное дифференциальное уравнение
. (3.11)
Решение этого уравнения может быть представлено как сумма двух решений: решения однородного уравнения
и частного решения для установившегося режима работы.
Общее решение для линейного дифференциального уравнения имеет вид
,
где С1, С2 – постоянные интегрирования,
– корни характеристического уравнения.
,
Отсюда 
При очень малом демпфировании, то есть при
, корни уравнения являются сопряженными комплексными корнями 
, где 
– коэффициент затухания; 
– угловая частота свободных колебаний ротора.
В этом случае общее решение может быть записано в виде
,
где 
– постоянные подлежащие определению.
Частное решение уравнения (3.11) соответствует установившемуся режиму, то есть 
. Так как в установившемся режиме
, 
, то 
.
Из начальных условий:
1) 
и при малом демпфировании (
) имеем
.
Откуда 
.
2) 
и так как , то 
. Откуда 
.
Окончательно колебания ротора при внезапном изменении внешнего момента можно записать в виде
|
|
|
.
Чем больше момент инерции, тем меньше 
, тем меньше частота собственных колебаний 
Гц.
При параллельной работе СМ возможно возникновение качания ротора. При этом если частота свободных колебаний ƒ0 близка к ƒ1, то возможно явление резонанса СМ, т.е. раскачивание ее. Поэтому, при расчете стремятся, чтобы ƒ0 значительно отличалась от ƒ1.
Следует иметь в виду, что чем частота 
близка к частоте свободных колебаний 
, то возможен резонанс, в результате которого происходит раскачивание машины и выход ее из синхронизма. Поэтому, при расчете следует исключать близость 
и .
|
|
|
