Свободные затухающие колебания. Логарифмический декремент. Апериодический процесс.

Свободные затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах. Q=W/DW

Решим данное уравнение:

Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами колеблющейся величины. Тогда период затухающих колебаний равен:

Если А(t) и А(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение называется декрементом затухания, а его логарифм - логарифмическим декрементом затухания; N_e – число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания – постоянная для данной колебательной системы величина.

При увеличении коэффициента затухания δ период затухающих колебаний растет и при δ=ω₀ обращается в бесконечность, т.е. движение перестает быть периодическим. В данном случае колеблющаяся величина асимптотически приближается к нулю, когда t→∞. Процесс не будет колебательным. Он называется апериодическим.

 

1.Уравнение движения свободных механических колебаний в присутствии сил вязкого трения имеет вид: d²x/dt²+2b dx/dt+w₀²x=0, где b - коэффициент затухания, w₀ - собственная циклическая частота.

2.Характер закона движения определяется величиной трения. Если трение мало (математически это выражается так: b <<w₀), то колебания похожи на гармонические, однако их амплитуда экспоненциально уменьшается со временем; и такие колебания называются затухающими. Быстрота затухания (диссипации энергии) характеризуется логарифмическим декрементом затухания, временем жизни колебаний, добротностью колебательной системы. Эти характеристики взаимосвязаны между собой. Если трение велико (b ³w₀), то движение становится апериодическим.

3.Закономерности свободных колебаний, установленные нами для механического движения, справедливы для колебаний любой физической природы, в частности, для электромагнитных колебаний в электрическом колебательном контуре, имеющем сопротивление.

 

Вынужденные колебания. Резонанс

Для получения незатухающих колебаний потери энергии колебаний на преодоление трения и сопротивления должны периодически компенсироваться, т.е., что колебательная система подвергается периодическому внешнему воздействию. Такие колебания называются вынужденными.

Уравнение движения:

ω – частота внешнего воздействия (вынужд. силы)

*) – Дифференциальное уравнение II порядка с правой частью.

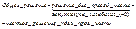
- в установившемся режиме

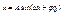**) – с частотой вынуждающей силы.

A, φ₀ – постоянные величины (они неизвестны). Найдем их. Они зависят не от н.у., а от m, r, k, ω, F₀.

**) → *)

- Амплитуда

- Фаза.

ω – растет; A ↑

ω → ∞; A → ∞ Система не успевает реагировать на F_вын, колебаний нет. A(ω) имеет максимум.

Резонанс.

Анализ зависимости А=A(ω) амплитуды от частоты вынужд. силы показывает, что система по разному откликается на внешнее воздействие и при определенной частоте этот отклик наибольший и амплитуда максимальная. Такое явление называется резонансом. Частота, при которой он наступает, называется резонансной ω_р.

ω_р -?

δ – коэффициент затухания: - зависит от сил трения.

Трение мало, δ мало. ω_р≤ω₀

А_р→∞ при δ →0

Резонансные кривые показаны на рисунке.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: