Электромагнитное поле. Уравнения Максвелла. Плоская электромагнитная волна.

Электромагнитная волна – это распространяющееся в пространстве электромагнитное поле. Оно может существовать в вакууме, поэтому электромагнитные волны могут распространяться в вакууме. Плоская электромагнитная волна представлена на рисунке.

Электромагнитные волны представляют собой распространяющееся в пространстве электромагнитное поле. Теоретически их существование было предсказано в 1865 г. Дж. К. Максвеллом, их экспериментальное наблюдение впервые осуществил Г. Герц в 1888 г.

Законы электромагнетизма, записанные в виде знаменитых уравнений Максвелла, констатируют механизм возникновения электрических и магнитных полей:

- электрическое поле создают во-первых, электрические заряды (это выражает теорема Гаусса), во-вторых, изменяющееся со временем магнитное поле (явление электромагнитной индукции);

- магнитное поле создают во-первых, движущиеся электрические заряды (токи), во-вторых, изменяющееся со временем электрическое поле.

Таким образом, электрические и магнитные поля взаимосвязаны друг с другом. Если в какой-либо области пространства возникнет переменное электрическое поле, то оно создаст переменное магнитное поле, которое, в свою очередь, индуцирует переменное электрическое поле и т. д. “Цепляясь” друг за друга, они образуют две неразрывные составляющие единого электромагнитного поля, которое может существовать в свободном пространстве (где нет ни зарядов, ни токов) в форме электромагнитных волн как самостоятельного вида материи. Применение уравнений Максвелла к подобной ситуации дает такие уравнения:

Напомним, что E и H - соответственно напряженности электрического и магнитного полей, e₀ и m₀ - электрическая и магнитная постоянные, e и m - диэлектрическая и магнитная проницаемость среды соответственно. Сравнивая формулы (2.12 a) и (2.12 б) с формулой (2.6), видим, что E и H представляют собой плоские бегущие волны вида (2.9), распространяющиеся с фазовой скоростью

u= 1/

В вакууме e =1, m =1, так что u= 1/ =1/ =3^.10 ⁸ м/с, т.е. любая электромагнитная волна в свободном пространстве распространяется со скоростью света с =3^.10⁸ м/с. Из этого свойства, в частности, следует, что в отличие от других видов материи, свободное электромагнитное поле не может находиться в состоянии покоя. В веществе скорость распространения u=с / . Решения волновых уравнений (2.12 a) и (2.12 б) имеют вид:

E=E_m sin(w t - 2px/l) H=H_m sin(w t - 2px/l) (2.14 б)

и являются плоской бегущей электромагнитной волной. Ее ”фотография”, т. е. распределение векторов напряженности электрического E и магнитного H полейвдоль луча в один и тот же момент времени представлена на рис. 2.3.

Перечислим свойства плоской электромагнитной волны:

1) В электромагнитной волне обязательно присутствуют оба поля E и H, при этом E ^ H.

2) Колебания электрического и магнитного полей в плоской электромагнитной волне происходят синфазно, при этом 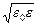E = H. Таким образом, для описания волны достаточно одного из двух уравнений (2.4a) или (2.4б).

3) Электромагнитные волны поперечные. Это означает, что колебания векторов E и H происходят перпендикулярно вектору скорости распространения волны u. Векторы u, E, H образуют правую тройку подобно ортам i, j, k, указывающим направление декартовых осей координат.

4) В вакууме скорость распространения электромагнитных волн любой частоты равна скорости света с= 3^.10⁸ м/с. Это, а также другие свойства электромагнитных волн доказывают, что свет является электромагнитной волной.

5) Электромагнитная волна, как и упругая, переносит энергию (возмущение)

 

Из уравнений Максвелла вытекает, что источниками электрического поля мо­гут быть либо электрические заряды, либо изменяющиеся во времени магнитные по­ля, а магнитные поля могут возбуждаться либо движущимися электрическими заря­дами (электрическими токами), либо пере­менными электрическими полями. Уравне­ния Максвелла не симметричны относи­тельно электрического и магнитного полей. Это связано с тем, что в природе су­ществуют электрические заряды, но нет зарядов магнитных.

 

 

10. Интерференция. Когерентность волн. Условия максимума и минимума интерференции. <?>Принцип получения когерентных световых волн<?>.

Интерференция волн

Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов связывают с по­нятием когерентности. Волныназываются когерентными, если разность их фаз оста­ется постоянной во времени. Очевидно, что когерентными могут быть лишь волны, имеющие одинаковую частоту. При нало­жении в пространстве двух (или несколь­ких) когерентных волн в разных его точ­ках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волн.

Рассмотрим механизм этого явления (рис. 3.2). Пусть S₁ и S ₂ – два источника, испускающие волны с одинаковыми частотами. В некоторой точке М, отстоящей от источников на расстоянии l₁ и l₂ соответственно, они возбуждают одинаково направленные колебания с амплитудами A₁ и A₂ и фазами φ₁ и φ₂. Амплитуда результирующего колебания(см. формулу 1.28)

A²=A₁²+A₂²+2A₁A₂cos(j₂-j₁)

Учитывая, что измеряемая интенсивность (см. формулу 3.2) в данной точке пропорциональна квадрату амплитуды волнового поля, получаем:

I=I₁+I₂+ 2 < cos(j₂-j₁)>.

Если разность фаз Δφ=j₂-j₁ со временем изменяется хаотически, то среднее за период колебаний значение < cos Δφ >=0, и в данной точке I=I₁+I₂. Получаем обычно наблюдаемый на опыте результат: энергия результирующей волны равна арифметической сумме энергий приходящих волн. Другими словами, если вместо одной лампочки мы включим две, то освещенность везде увеличится вдвое.

Рассмотрим наложение двух когерент­ных сферических волн, возбуждаемых то­чечными источниками S₁ и S₂ (рис.221), колеблющимися с одинаковыми амплиту­дой ао и частотой СО и постоянной разно­стью фаз. Согласно уравнению сферической волны :

,

где r ₁ и r ₂ — расстояния от источников волн до рассматриваемой точки В, k — волновое число, (j₁ и j₂ — начальные фазы обеих накладывающихся сферических волн. Амплитуда результирующей волны в точке В равна:

Так как для когерентных источников разность начальных фаз (j₁-j₂)=const, то результат наложения двух волн в различных точках зависит от величи­ны D= r ₁- r ₂, называемой разностью хо­да волн.

В точках, где k (r ₁ -r ₂ )- (j₁-j₂)=±2mp (m=0, 1,2,...), наблюдается интерференционный макси­мум: амплитуда результирующего колеба­ния A=A ₀ /r ₁ +A₀/r ₂.

В точках, где k (r ₁- r ₂) - (j₁-j₂)= ±(2m+1)p (m=0, 1,2,...), наблюдается интерференционный мини­мум: амплитуда результирующего колеба­ния А=А ₀ /r ₁ —А ₀ /r ₂│(m=0, 1, 2,...,) называется соответственно порядком ин­терференционного максимума или мини­мума.

Эти Условия сводятся к тому, что r ₁ -r ₂=const.

Интерференция света

Возникает при сложении двух (или более) световых волн, когда в одних местах волны гасят друг друга, а в других – усиливают, т.е. происходит перераспределение энергии вдоль фронта волны с образованием максимумов и минимумов интенсивности. Для световых волн максимумы ярко освещены, минимумы – слабо (темные области). Интерференционная картина устойчива во времени.

- условие максимума, (m=0, 1, 2,…);

- условие минимума.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: