 |
Понятие выборочного метода
|
|
|
|
Выборочный метод ¾ это такое несплошное наблюдение, при котором подлежащие обследованию единицы отбираются в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность.
Совокупность, из которой проводится отбор, называется генеральной (все обобщающие показатели совокупности ¾ генеральными). Совокупность отобранных единиц именуют выборочной, а ее обобщающие показатели ¾ выборочными.
Применяя выборочный метод, обычно используют два вида обобщающих показателей: среднюю величину количественного признака и относительную величину альтернативного признака (долю единиц, обладающую тем или иным признаком).
Приведем обозначения основных характеристик параметров генеральной и выборочной совокупностей (табл. 10.1).
Таблица 10.1
Обозначения основных характеристик параметров
генеральной и выборочной совокупностей
Ошибки, возникающие при выборочном наблюдении
Основная задача выборочного наблюдения в экономике состоит в том, чтобы на основе характеристик выборочной совокупности (средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности. При решении этой задачи возникают ошибки двух видов: регистрации и репрезентативности (рис. 10.1). Ошибки репрезентативности присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную.
Рис. 10.1. Виды ошибок при выборочном наблюдении
Степень точности выборочных оценок зависит от величины ошибки репрезентативности. В общем виде ошибка репрезентативности, или предельная ошибка выборки, характеризуется величиной расхождения параметров выборочной и генеральной совокупностей. Так, для средней величины имеем:
|
|
|
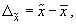
где 
¾предельная ошибка выборки;
¾выборочная средняя;
¾генеральная средняя.
Величина предельной ошибки выборки в соответствии с теоремами теории вероятностей будет кратна средней ошибке:
где t ¾ нормированные отклонения, зависящие от вероятности, с которой гарантируется результат;
m ¾ средняя квадратическая стандартная ошибка выборки.
Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:
■ для средней: 
■ для доли: p = w ± D w; w - D w £ p £ w + D w.
Это означает, что с заданной вероятностью можно утверждать, что значение генеральной средней следует ожидать в пределах от 
до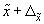 
.
Аналогичным образом может быть записан доверительный интервал генеральной доли:
w - D w; w + D w.
Значения вероятности (функция Ф (t))при различных значениях t определяются на основе специально составленных таблиц. Приведем некоторые значения, применяемые наиболее часто для выборок достаточно большого объема (n ³ 30):
Классификация выборок
Виды выборок различаются в зависимости от вида метода и способа отбора, а также степени охвата единиц совокупности (рис. 10.2).
При повторном отборе общая численность единиц генеральной совокупности остается неизменной. Та или иная единица, попавшая в выборку, после регистрации возвращается в генеральную совокупность и сохраняет равную возможность со всеми прочими единицами при повторном отборе вновь попасть в выборку.
При бесповторном отборе единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует. Таким образом, численность единиц генеральной совокупности сокращается в процессе отбора.
К собственно-случайной выборке относится отбор единиц из всей генеральной совокупности (без предварительного расчленения ее на группы) посредством жеребьевки (преимущественно) или иного подобного способа, например с помощью таблицы случайных чисел.
|
|
|
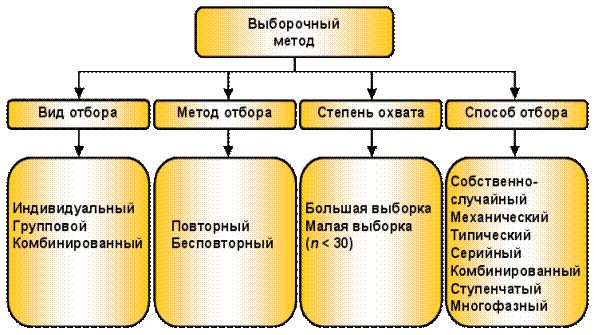
Рис. 10.2. Виды выборок
Средняя и предельная ошибки собственно-случайной выборки вычисляются по следующим формулам (табл. 10.2).
Таблица 10.2
|
|
|
