 |
Формулы ошибок собственно-случайной выборки
|
|
|
|
Рекомендация:
Обратитесь к примерам по указанным ссылкам: пример 10.3.1.
Механическая выборка применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т. е. имеется определенная последовательность в расположении единиц (табельные номера работников, телефонные номера респондентов и т. д.). Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей. Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы. Например, при пропорции 1: 50 (2%-ная выборка) отбирается каждая 50-я единица, при пропорции 1: 20 (5%-ная выборка) отбирается каждая 20-я единица.
Для определения средней ошибки механической выборки используется формула средней ошибки при собственно-случайном бесповторном отборе.
Рекомендация:
Обратитесь к примерам по указанным ссылкам: пример 10.3.2.
Типический отбор используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп. Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки, которая в этом случае определяется только внутригрупповой вариацией.
Отбор единиц в типическую выборку может быть организован либо пропорционально объему типических групп, либо пропорционально внутригрупповой дифференциации признака.
|
|
|
При выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:
где Ni ¾ объем i -й группы;
ni ¾ объем выборки из i -й группы.
При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле
где s i ¾ среднее квадратическое отклонение значений признака в i -й группе.
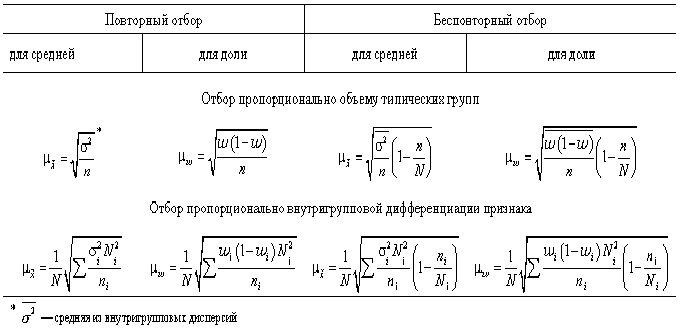
В таком случае средняя ошибка выборки будет определяться по следующим формулам (табл. 10.3).
Таблица 10.3
Формула средней ошибки при типической выборке
Рекомендация:
Обратитесь к примерам по указанным ссылкам: пример 10.3.3.
Серийный отбор удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. Сущность серийной выборки заключается в собственно-случайном либо механическом отборе серий, внутри которых проводится сплошное обследование единиц.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам (табл. 10.4).
Таблица 10.4
Формулы ошибок при серийной выборке
(отбор пропорционально объему типических групп)
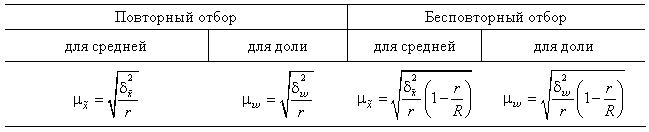
где r ¾ число отобранных серий;
R ¾ общее число серий;
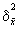¾межгрупповая дисперсия количественного признака;
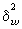¾межгрупповая дисперсия доли.
Межгрупповую дисперсию вычисляют следующим образом:
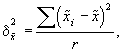
где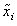 
¾средняя i -й серии;
¾общая средняя по всей выборочной совокупности;
где wi ¾ доля признака в i -й серии;
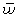¾общая доля признака во всей выборочной совокупности.
Рекомендация:
Обратитесь к примерам по указанным ссылкам: пример 10.3.4.
|
|
|
