Алгоритм нахождения сильных компонент графа можно описать следующей последовательностью шагов

Шаг 1. G = (X, V) – данный граф. Определение сильных компонент графа (СК) начать с произвольной вершины х_i Î Х. Найти R (x_i) и Q (x_i). Положить СК(х_i) = - сильная компонента графа, содержащая вершину х_i.

Шаг 2. Определить множество . Если ¹Æ, то и перейти к шагу 1, иначе останов, так как все сильные компоненты определены.

 

Граф G*= (X*,V *) определяется так: каждая его вершина представляет множество вершин некоторой сильной компоненты графа G, дуга (x_i *, x_j *) существует в G * тогда и только тогда, когда в G существует дуга (x_i, x_j), такая, что x_i принадлежит ком­поненте, соответствующей вершине x_i *, а x_j –компоненте, соответствующей вершине x_j*. Граф G* называют конденсацией графа G.

Совершенно очевидно, что конденсация G* не содержит контуров, поскольку наличие контура означает, что любые вершины этого контура взаимно достижимы. Поэтому совокупность всех вершин контура принадлежит некоторой СК в G* и, следовательно, содержится в СК графа G, что противоречит определению конденсации, в силу которого вершины из G * соответствуют СК в G.

Пример. Для графа G, приведенного на рис. 4.25, найти сильные ком­поненты и построить конденсацию G *.

 

 

 

Найдем СК в G, содержащую вершину x ₁.

Из соотношений (4.3) и (4.4) получаем

R (x ₁) ={ x ₁, x ₂, x ₄, x ₅, x ₆ , x ₇, x ₈, x ₉, x ₁₀ }

Q (x ₁) ={ x ₁, x ₂, x ₃, x ₅, x ₆ }

Следовательно, СК, содержащая вершину x ₁, является порожденным подграфом

R (x ₁) Q (x ₁) = ({ x ₁, x ₂, x ₅, x ₆ })

Аналогично, СК, содержащая вершину x ₈, есть порожденный подграф ({ x ₈, x ₁₀}), СК содержащая x ₇ – подграф ({ x ₄, x ₇, x ₉}), СК, содержащая x ₁₁, –подграф ({ x ₁₁, x ₁₂, x ₁₃ }) и СК, содержащая x ₃, – подграф ({ x ₃}). Следует отметить, что последняя СК со­стоит из единственной вершины графа G. Конденсация G* приведена на рис. 4.26.

 

Рис. 4.26. G * - конденсация графа G

 

Процедуру, описанную выше и связанную с нахождением СК графа, можно сделать более удобной, если непосредственно исполь­зовать матрицы R и Q. Пусть запись R Ä Q означает поэлементное умножение этих матриц. Тогда сразу видно, что строка x_i, матрицы R Ä Q содержит единицы только в тех столбцах x_j, для которых выполняется усло­вие: вершины x_i и x_j взаимно достижимы; в других местах строки x_i стоят нули. Таким образом, две вершины находятся в одной и той же СК тогда и только тогда, когда соответствующие им стро­ки (или столбцы) в матрице R Ä Q идентичны. Вершины, кото­рым соответствуют строки, содержащие 1 в столбце x_j, образуют множество вершин СК, содержащей x_j. Отсюда мгновенно сле­дует, что матрицу R Ä Q можно преобразовать путем транспони­рования строк и столбцов в блочно-диагональную. Каждая из диа­гональных подматриц этой матрицы соответствует СК графа G и содержит только единичные элементы, все остальные элементы блочно-диагональной матрицы равны нулю. Для приведенного ранее примера матрица R Ä Q, преобразованная соответствую­щим образом, имеет вид

 

	x 1 x 2 x 5 x 6	x 8 x 10	x 4 x 7 x 9	x 11 x 12 x 13	x 3
x 1 x 2 x 5 x 6	1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
x 8 R Ä Q = x 10		1 1   1 1
x 4 x 7 x 9			1 1 1 1 1 1 1 1 1
x 11 x 12 x 13				1 1 1 1 1 1 1 1 1
x 3

Таким образом, сильные компоненты графа можно находить по следующему алгоритму.

Шаг 1. G – данный граф. Для G построить матрицу достижимости R и найти матрицу контрдостижимости, транспонировав матрицу R, Q = R^T.

Шаг 2. Получить матрицу C, осуществив поэлементное умножение матриц R и Q, т.е. С = R Ä Q, где Ä – поэлементное умножение матриц.

Шаг 3. Преобразовать матрицу С к блочно-диагональ-ному виду путем перестановки строк и столбцов. Каждая из диагональных подматриц соответствует сильной компоненте графа G. Останов.

Базы и антибазы

База или вершинная база В есть множество вершин графа G, из которого достижима любая вершина графа и которое является минимальным в том смысле, что не существует собственного подмножества в В, обладающего таким свойством достижимости.

Базой является такое множество вершин графа G, которое удовлетворяет следующим двум условиям:

1) каждая вершина графа G достижима хотя бы из одной вершины множества В;

2) в В нет вершины, которая достижима из другой вершины множества В.

Из этих условий получаются следующие утверждения.

1. В множестве В нет двух вершин, которые принадлежат одной и той же СК графа G.

2. В любом графе без контуров существует единственная база. Она состоит из всех таких вершин, полустепени захода которых равны 0.

Доказательства этих утверждений простые и непосредственно следуют из определений. Утверждения позволяют сформировать алгоритм нахождения баз ориентированного графа, который описывает следующая последовательность шагов.

Шаг 1. G – данный граф. Для G найти все сильные компоненты.

Шаг 2. Построить конденсацию G * графа G.

Шаг 3. Определить базу В * конденсации G *, включив в В * те вершины G *, полустепени захода которых равны 0.

Шаг 4. Построить базу В графа G из В *, взяв по одной вершине из сильных компонент, входящих в В *. Останов.

Пример. Для графа G, приведенного на рис. 4.25, конденсация показана на рис. 4.26. Базой графа G * является множества , поскольку и - единственные вершины в графе G * с полустепенями захода, равными 0. Базами графа G являются , и .

Понятие, двойственное понятию базы есть антибаза. Антибаза графа G есть такое минимально возможное множестве вершин, что какова бы ни была вершина графа G, из нее достижима некоторая вершина в . Свойства антибаз аналогичны свойствам баз, надо только «прямые» понятия заменить на двойственные. Опишем алгоритм нахождения антибаз графа.

Шаг 1. G - данный граф. Для G найти все сильные компоненты.

Шаг 2. Построить конденсацию G * графа G.

Шаг 3. Определить антибазу ` В * конденсации G *, включив в` В * те вершины G *, полустепени исхода которых равны 0.

Шаг 4. Построить антибазу графа G из ` В *, взяв по одной вершине из сильных компонент, входящих в` В *. Останов.

В примере с графом G, изображенным на рис. 4.25, конденсация графа G * (рис. 4.26) содержит только одну вершину с полустепенью исхода, равной 0. Таким образом, антибаза графа G * , а антибазами графа G являются множества 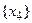, и .

Понятия связности и достижимости применяют к исследованию структуры организаций. Например, если граф представляет структуру руководства или влияний некоторой организации, то элементы каждой сильной компоненты имеют равную власть и равное влияние друг на друга. Базу графа можно интерпретировать как «коалицию», включающую наименьшее число лиц, обладающих властью над каждым членом организации.

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: