 |
Функции, отображения и операции
|
|
|
|
Рассмотрим два множества X и Y. Если для каждого элемента  указан элемент
указан элемент 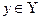 , то говорят, что между множествами X и Y установлено соответствие. Обозначим его через Г. Тогда Г состоит из множества упорядоченных пар (x, y), таких, что
, то говорят, что между множествами X и Y установлено соответствие. Обозначим его через Г. Тогда Г состоит из множества упорядоченных пар (x, y), таких, что  и y
и y  Y: Г
Y: Г 
 . При этом совершенно необязательно, чтобы в сопоставлении участвовали все элементы множества X и Y.
. При этом совершенно необязательно, чтобы в сопоставлении участвовали все элементы множества X и Y.
Образом элемента x при соответствии Г называется множество Im(x), такое что
Im(x)={ y  (x, y)
(x, y)  }.
}.
Прообразом элемента y при соответствии Г называется множество
Coim(y)={ x  (x, y)
(x, y)  }.
}.
Областью значений соответствия Г называется множество 
Областью определения соответствия Г называется множество  .
.
Для каждого соответствия существует обратное соответствие 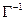 , которое любому y
, которое любому y  Y сопоставляет x
Y сопоставляет x  X, причем
X, причем 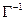 ={(y, x)
={(y, x)  (x, y)
(x, y)  }.
}.
Отображением (однозначным)  называется такое соответствие, которое каждому х
называется такое соответствие, которое каждому х  Х сопоставляет единственный элемент у
Х сопоставляет единственный элемент у  Y. При отображении
Y. При отображении  соответствие между х и у записывается в виде у =
соответствие между х и у записывается в виде у =  (x), a само отображение определяет запись
(x), a само отображение определяет запись  : X
: X  Y, при этом Х называется областью определения отображения, Y – областью значений.
Y, при этом Х называется областью определения отображения, Y – областью значений.
Два отображения  : X
: X 
 Y
Y 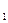 , и
, и  : X
: X 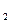
 Y
Y 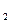 равны, если для всех х
равны, если для всех х  Х, X
Х, X 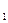 = X
= X 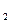 , Y
, Y 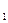 = Y
= Y 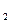 и
и  =
=  .
.
Отображение называется многозначным, если некоторым значениям х  Х соответствуют подмножества Y
Х соответствуют подмножества Y 
 Y, состоящие более чем из одного элемента.
Y, состоящие более чем из одного элемента.
Если Х – область определения, а Y – область значений отображения  , то говорят, что
, то говорят, что  отображает Х на Y. Если
отображает Х на Y. Если  отображает Х на Y и Y
отображает Х на Y и Y  Z, то говорят, что
Z, то говорят, что  отображает Х в Z.
отображает Х в Z.
Поскольку отображение является частным случаем соответствия, то можно ввести понятие обратного отображения.
Если заданы три множества X, Y, Z и на Х определено отображение f со значениями в Y, а на Y задано отображение g со значениями в Z, то существует отображение h с областью определения в X, принимающее значения в Z и определяемое равенством h (x)= g (f (x)). Это отображение называется композицией отображений g и f или сложным отображением, составленным из внутреннего отображения f и внешнего отображения g.
|
|
|
Рассмотрим некоторые свойства отображений.
Отображение  : X
: X  Y называется сюрьективным, или сюръекцией, если любой y
Y называется сюрьективным, или сюръекцией, если любой y  Y есть образ по крайней мере одного х
Y есть образ по крайней мере одного х  Х. Заметим, что условие
Х. Заметим, что условие 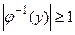 для любого у или | Х |
для любого у или | Х | 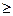 | Y | характеризует сюръекцию.
| Y | характеризует сюръекцию.
Пример. Отображение  : {1, 2, 3, 4}
: {1, 2, 3, 4}  { у
{ у 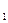 , у
, у 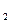 , y
, y 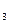 }, такое что
}, такое что  ,
,  ,
, 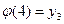 сюръективно. Отображение
сюръективно. Отображение  : {1, 2, 3, 4}
: {1, 2, 3, 4}  { у
{ у 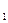 , у
, у 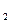 , y
, y 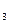 } с условиями
} с условиями  ,
,  не является сюрьективным.
не является сюрьективным.
Отображение  : X
: X  Y называется инъективным, или инъекцией, если каждый элемент y
Y называется инъективным, или инъекцией, если каждый элемент y  Y имеет хотя бы один прообраз х
Y имеет хотя бы один прообраз х  Х либо вообще не имеет прообраза. Можно видеть, что условие
Х либо вообще не имеет прообраза. Можно видеть, что условие  для любого y
для любого y  Y или
Y или 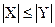 определяют инъекцию.
определяют инъекцию.
Пример. Пусть Х = {1, 2, 3}, Y = { у 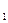 , у
, у 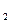 , y
, y 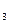 ,
,  }, Отображение
}, Отображение  :
:  инъективно, если
инъективно, если  ,
,  ,
,  .
.
Если отображение одновременно является сюръективным и инъективным, то оно называется биективным отображением или биекцией. Для биективного отображения  = 1 для любого у или
= 1 для любого у или  .
.
Пример. 3.3. Пусть Х= {1, 2,3}, Y ={ у 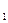 , у
, у 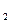 , y
, y 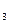 }. Отображение
}. Отображение  биективно, если
биективно, если  ,
,  ,
,  .
.
Биективное отображение определяет взаимно однозначное соответствие между множествами Х и Y. Если между Х и Y можно установить взаимно однозначное соответствие, то множество Х называется эквивалентным множеству Y. Установление взаимно однозначного соответствия между множествами играет важную роль. Так, определение числа элементов конечного множества X, то есть установление равенства  n при некотором n, фактически сводится к отысканию некоторого взаимно однозначного соответствия между множествами Х и N ={1,2,... n }. Множества, равномощные N, называются счетными. Множества равномощны, если между их элементами можно установить взаимно однозначное соответствие, то есть эквивалентные множества являются равномощными.
n при некотором n, фактически сводится к отысканию некоторого взаимно однозначного соответствия между множествами Х и N ={1,2,... n }. Множества, равномощные N, называются счетными. Множества равномощны, если между их элементами можно установить взаимно однозначное соответствие, то есть эквивалентные множества являются равномощными.
|
|
|
Отображение 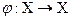 представляет собой отображение самого множества в себя и называется преобразованием множества Х.
представляет собой отображение самого множества в себя и называется преобразованием множества Х.
Пусть f  – соответствие между множествами Х и Y. Если для каждого х, такого что (х, у)
– соответствие между множествами Х и Y. Если для каждого х, такого что (х, у)  f, имеется единственный образ, то соответствие называется функциональным и определяет функцию f на множестве Х со значениями в множестве Y. Задание функции означает, что определено отображение f:
f, имеется единственный образ, то соответствие называется функциональным и определяет функцию f на множестве Х со значениями в множестве Y. Задание функции означает, что определено отображение f: 
 Y, где
Y, где 
 , а для элементов множества
, а для элементов множества  отображение, а значит, и функция f не определены. Значение у в любой из пар (х, у)
отображение, а значит, и функция f не определены. Значение у в любой из пар (х, у)  f называется функцией от данного х, что записывается в виде у = f (x).
f называется функцией от данного х, что записывается в виде у = f (x).
На функцию переносятся все рассмотренные свойства отображений, при этом считается, что функция обладает некоторым свойством, если этим свойством обладает соответствующее отображение. Две функции равны, если равны соответствующие им отображения. Функция может быть сюръективной, инъективной или биективной. Функция f, для которой из f (x)= f (y) следует x = у, называется взаимно однозначной. Кроме того, для функции можно ввести понятия обратной функции, композиции функций, которая в этом случае называется суперпозицией.
Примеры. 1.Рассмотрим три функции  , i =1,2,3:
, i =1,2,3:
1) функция  инъективна, но не сюрьективна;
инъективна, но не сюрьективна;
2) функция  сюрьективна, но не инъективна;
сюрьективна, но не инъективна;
3) функция  биективна.
биективна.
2. Биекцией между множеством натуральных чисел N и множеством целых чисел Z является функция  , для которой
, для которой 
К специальным отображениям относятся понятия оператора и функционала.
Оператор - отображение одного множества на другое, каждое из которых наделено некоторой структурой.
Функционал - отображение произвольного множества Х в множество комплексных или действительных чисел.
Если множество Х в определении функции у = f (x) является декартовым произведением n множеств X 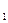 , X
, X 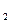 ,..., Xn, то получаем определение n -местной функции у =
,..., Xn, то получаем определение n -местной функции у = 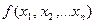
 , Частным случаем n -местной функции является n -местаая операция - n -местная функция, у которой области определения аргументов и область значений совпадают, то есть
, Частным случаем n -местной функции является n -местаая операция - n -местная функция, у которой области определения аргументов и область значений совпадают, то есть  . Таким образом, n -местная операция по n элементам множества Х определяет (n +1)-й элемент этого же множества.
. Таким образом, n -местная операция по n элементам множества Х определяет (n +1)-й элемент этого же множества.
Пример. Сложение, умножение и разность действительных чисел является примерами операций на множестве действительных чисел. Разность двух неотрицательных чисел не является операцией на множестве неотрицательных чисел.
|
|
|
Рассмотрим некоторые свойства бинарных операций.
Операция  называется
называется
коммутативной, если для любых x, y из множества Х
 ;
;
ассоциативной, если для любых x, y, z из множества Х
 ;
;
дистрибутивной относительно операции 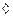 , если для любых x, y, z из множества Х для операций выполняются соотношения
, если для любых x, y, z из множества Х для операций выполняются соотношения
 или
или  .
.
Замечание. Коммутативность операции означает независимость результата операции от перемены мест аргументов. Ассоциативность означает, что если выражение включает некоторую ассоциативную операцию, то последовательность действий при получении результата может быть произвольной. Известные арифметические операции сложения и умножения чисел являются ассоциативными и коммутативными.
ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
Основу теории графов составляет совокупность методов и представлений, сформировавшихся при решении конкретных задач.
Термин «граф» впервые появился в книге выдающегося венгерского математика Д. Кёнига в 1936 г., хотя начальные задачи теории графов восходят еще к Эйлеру (XVIII в.). Одна из задач, положивших начало теории графов, – задача о кенигсбергских мостах будет рассмотрена в разделе 4.12.
Граф есть совокупность точек и линий, соединяющих эти точки. Эти соединения могут обладать различными характеристиками, и теория графов занимается изучением этих характеристик. Граф характеризует отношения между множествами объектов.
Большое значение в теории графов имеет проблема разрешимости: найти эффективный или хотя бы достаточно простой в практически важных случаях алгоритм решения задачи.
В последнее время теория графов принимает все более прикладной характер, являясь эффективным аппаратом для формализации множества задач, связанных с дискретным размещением объектов. К ним, в частности, относятся: проектирование и исследование сетей связи, анализ электрических цепей, графы потока сигналов и теория обратной связи, блок-схемы программы, исследование автоматов, анализ и синтез логических цепей, задачи календарного планирования, планирование и обеспечение материально-технического снабжения, поиск информации, стратегия инвестиций, анализ качества, исследование движения транспорта, размещение предприятий коммунального обслуживания, моделирование, экономические задачи, теория игр, головоломки, доказательство теорем.
|
|
|
Основные понятия и определения теории графов
Пусть задано некоторое конечное множество X, элементы которого будем называть вершинами, и множество V, состоящее из пар элементов (xi, xj) множества X. Упорядоченная пара множеств G=(X, V) называется графом. Вершины изображаются точками, а пары элементов – линиями, соединяющими точки, соответствующие образующим пары вершинам.
Если в определении графа существенно в каком порядке выбираются вершины (то есть пара (xi, xj) отлична от пары (xj, xi)), то такой граф называют ориентированным илиорграфом, а пару (xi, xj)–дугой, при этом считается, что хi –начальная вершина, a xj – конечная. В геометрической интерпретации дуге соответствует направленный отрезок. Часто орграф задают парой G=(X, Г), где Х – множество вершин, а Г – неоднозначное отображение, ставящее в соответствие каждой вершине подмножество в X. Г(хi)– множество вершин хj Î Х, для которых в графе G существует дуга (хi, хj).  (хi)– множество вершин хj Î X, для которых в графе G существует дуга (xj, хi).
(хi)– множество вершин хj Î X, для которых в графе G существует дуга (xj, хi).
Если в определении графа не существенен порядок вершин при образовании пары (хi, xj), то граф называют неориентированным или неорграфом, а пару (xi, xj) – ребром.
Число вершин графа называется его порядком.
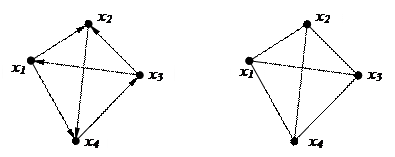
 Пример. На рис. 4.1 изображен ориентированный граф G =({ x 1, x 2, x 3, x 4}, {(x 1, x 2), (x 1, x 4), (x 2, x 4), (x 3, x 1), (x 3, x 2), (x 4, x 3)}), а на рис. 4.2 – неориентированный граф.
Пример. На рис. 4.1 изображен ориентированный граф G =({ x 1, x 2, x 3, x 4}, {(x 1, x 2), (x 1, x 4), (x 2, x 4), (x 3, x 1), (x 3, x 2), (x 4, x 3)}), а на рис. 4.2 – неориентированный граф.
Рис. 4.1 Рис. 4.2
Путем в графе G называется такая последовательность дуг, в которой конец каждой предыдущей дуги совпадает с началом следующей. Для неорграфа такая последовательность ребер называется цепью. Если путь (цепь) проходит через вершины х 1,..., хk, то будем обозначать его (ее) символом [ x 1, …, xk ].
Для графа на рис. 4.1 последовательность дуг (x1, x2), (x2, x4), (x4, x3) является путем и может быть обозначена следующим образом [ x1, x2, x4, x3 ]. Для графа на рис. 4.2 цепью является, например, следующая последовательность ребер (x2, x3), (x3, x5), (x5, x4), которую обозначим через [ x2, x3, x5, x4 ].
Путь (цепь), у которого(-ой) начальная и конечная вершина совпадают, называется контуром (циклом). Для графа на рис. 4.2 циклом является, например, следующая цепь [ x2, x3, x5, x1, x2 ].
Простым циклом графа называется цикл, в котором все вершины различны за исключением начальной и конечной вершины, которые совпадают. Например, для графа на рис. 4.2 цикл [ x2, x3, x5, x1, x2 ] является простым, а цикл [ x2, x3, x4, x5, x3, x1, x2 ] не является простым.
|
|
|
Петлей называется дуга, начальная и конечная вершины которой совпадают.
Граф, полученный из орграфа заменой каждой дуги на ребро, называется основанием орграфа.
Пример. На рис. 4.3.б изображен граф, который является основание графа, изображенного на рис. 4.3.а.
Две вершины хi и хj называются смежными, если существует соединяющее их ребро (дуга) (хi, xj), при этом вершины называются инцидентными этому ребру (дуге), а ребро (дуга) – инцидентным(-ой) этим вершинам. Аналогично, два различных ребра (дуги) называются смежными, если они имеют по крайней мере одну общую вершину.
а б
Рис. 4.3
Вершины х 1 и х 4 смежны (рис. 4.3), дуга (х 1, х 4) инцидентна вершинам х 1 и х 4, а вершины х 1 и х 4 инцидентны дуге (х 1, х 4). Ребра (х 1, х 3) и (х 3, х 4) смежны (рис. 4.2).
Замечание. Смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.
Множество всех вершин графа G, смежных с некоторой вершиной x, называется окружением вершины x и обозначается через NG(x) или просто N(x).
В неориентированном графе число ребер, инцидентных данной вершине хi, называется степенью (валентностью) вершины хi и обозначается d (хi). Вершина графа, имеющая степень 0, называется изолированной, а вершина, имеющая степень 1 – висячей. Для неорграфа на рис. 4.2 d (х 1)=3, d (х 3)=4.
Число дуг, исходящих из вершины хi ориентированного графа, называется полустепенью исхода вершины хi и обозначается  . Число дуг, заходящих в вершину хi ориентированного графа, называется полустепенью захода вершины хi и обозначается
. Число дуг, заходящих в вершину хi ориентированного графа, называется полустепенью захода вершины хi и обозначается  . Так, для орграфа, представленного на рис. 4.3.а)
. Так, для орграфа, представленного на рис. 4.3.а)  ,
,  .
.
Утверждение (лемма о рукопожатиях). Сумма степеней вершин графа G равна 2 m, где m – число ребер графа G.
Доказательство. Поскольку каждое ребро инцидентно двум вершинам, то оно добавляет двойку к сумме степеней графа G. Следовательно, все ребра дают вместе сумму степеней 2 m.
Подграфом графа G=(X,V) называется граф G'=(X',V'), для которого X'ÍX, V'ÍV, причемребро (xi, xj) содержится в V' только в том случае, если xi и xj содержатся в X'. Одним из подграфов графа на рис. 4.1 является следующий (рис. 4.4)
Если все вершины графа G=(X,V) присутствуют в подграфе G'=(X',V'), тогда G' называется остовным подграфом, т. е. X'=Х, V'ÍV.
Пусть X' – подмножество вершин Х графа G=(X,V). Тогда граф G'=(X',V') называется порожденным подграфом графа G на множестве вершин X' (вершинно-порожденный подграф), если V' является таким подмножеством V, что ребро (xi, xj) входит в V' тогда и только тогда, когда xi и xj входят в X'.
 На рис. 4.5 представлен порожденный подграф на множестве вершин { х 1, х 3, x 5} неориентированного графа, изображенного на рис 4.2.
На рис. 4.5 представлен порожденный подграф на множестве вершин { х 1, х 3, x 5} неориентированного графа, изображенного на рис 4.2.
Рис. 4.4 Рис. 4.5
Типы графов
Граф G называется полным, если любые две его вершины смежны.Полный граф порядка n обозначается символом Кn, число ребер в нем равно 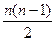 . На рис. 4.6 изображены графы Кn, n £5.
. На рис. 4.6 изображены графы Кn, n £5.
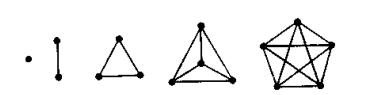 |
Рис. 4.6
Граф называется пустым, если в нем нет ребер. Пустой граф порядка n обозначается через Оn.
Граф, не содержащий вершин и, следовательно, ребер, называется ноль-графом. Граф, состоящий из одной вершины, называется тривиальным.
Красивыми примерами являются графы пяти платоновых тел (т. е. правильных многогранников): тетраэдра, куба, октаэдра, додекаэдра, икосаэдра (рис. 4.7).
Граф называется двудольным, если существует такое разбиение множества его вершин на две части (доли), что концы каждого ребра принадлежат разным частям. Если при этом любые две вершины, входящие в разные доли, смежны, то граф называется полным двудольным. Полный двудольный граф, доли которого состоят из р и из q вершин, обозначается символом K p,q . При р =1 получаем звезду K1,q. На рис. 4.8 изображены звезда К1,5 и полный двудольный граф K3,3.
Аналогично двудольным графам определяются k-дольный и полный k-дольный графы для k= 3, 4,... На рис. 4.9 приведен трехдольный граф.
Икосаэдр
 |
| Тетраэдр Куб Октаэдр Додекаэдр |
Рис. 4.7

Рис. 4.8 Рис. 4.9
Легко подсчитать число всех графов с фиксированным множеством вершин X. Эти графы различаются своими ребрами, и потому их число равно количеству подмножеств в X(2), т.е. 2  , где п= |X|. Однако эти графы не всегда следует различать. Как в применениях теории графов, так и в самой этой теории чаще существенно лишь то, что есть объекты (вершины графа) и связи между объектами (ребра). С этих позиций графы, которые получаются один из другого изменением наименований вершин, разумно не различать.
, где п= |X|. Однако эти графы не всегда следует различать. Как в применениях теории графов, так и в самой этой теории чаще существенно лишь то, что есть объекты (вершины графа) и связи между объектами (ребра). С этих позиций графы, которые получаются один из другого изменением наименований вершин, разумно не различать.
Два графа G1 и G2 называютсяизоморфными, если существует взаимно-однозначное отображение между множествами их вершин, сохраняющее смежность. Такое отображение называетсяизоморфизмом. Два орграфа изоморфны, если существует изоморфизм между их основаниями, сохраняющий порядок вершин на каждой дуге.
Например, три графа, представленные на рис. 4.10, изоморфны, а графы на рис. 4.11 не изоморфны. Вопрос о том, изоморфны ли два данных графа, в общем случае оказывается сложным.

Рис. 4.10

Рис. 4.11
Очевидно, что отношение изоморфизма графов является эквивалентностью, т. е. оно рефлексивно, симметрично и транзитивно. Следовательно, множество всех графов разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны. Изоморфные графы можно отождествлять, т. е. считать совпадающими (их можно изобразить одним рисунком). Они могли бы различаться конкретной природой своих элементов, но именно это игнорируется при введении понятия «граф».
В некоторых ситуациях все же приходится различать изоморфные графы, и тогда полезно понятие «помеченный граф». Граф порядка п называется помеченным, если его вершинам присвоены некоторые метки, например, номера 1, 2,..., n. Отождествив каждую из вершин графа с ее номером (и, следовательно, множество вершин – с множеством чисел {1, 2,..., n }), определим равенство помеченных графов G1=(X,V1) и G2=(X,V2) одного и того же порядка: G1=G2 тогда, когда V1=V2. На рис. 4.12 изображены три разных помеченных графа.
При необходимости подчеркнуть, что рассматриваемые графы различаются лишь с точностью до изоморфизма, говорят: «абстрактный граф». Строго говоря, абстрактный (или непомеченный) граф – это класс изоморфных графов.
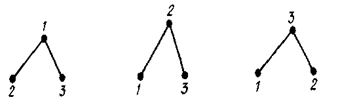
Рис. 4.12
Если вершины графа соединены более чем одним ребром, то такой граф называетсямультиграфом, а ребра – кратными. Мультиграф не допускает петель.
Граф,не содержащий петельи кратных ребер, называется простым.
Граф G=(X,V) называется симметрическим, если в V для любой дуги (xi, xj) существует противоположно ориентированная дуга (xj, хi). Условимся в этом случае соединять обе вершины одной непрерывной линией без стрелок.
Граф называетсяантисимметрическим, если каждая пара смежных вершин соединена только в одном направлении и петли отсутствуют.
Граф, у которого все вершины имеют одну и ту же степень, называетсярегулярным (однородным) графом. Если степень каждой вершины равна r, то граф называется регулярным (однородным) степени r. На рис. 4.10 изображены регулярные графы степени 3.
Граф, который можно изобразить на плоскости так, чтобы никакие два ребра не пересекались в точках, отличных от вершин, называется планарным графом.
Реберным графом L(G) простого графа G называется граф, вершины которого взаимно однозначно сопоставлены ребрам графа G, причем две вершины в L(G) смежны тогда и только тогда, когда соответствующие им ребра смежны в G.
Орграф G' называется обратным к данному орграфу G, если он имеет те же вершины, что и G, а дуга (xi, xj) принадлежит G' тогда и только тогда, когда дуга (xj, хi) принадлежит G.
|
|
|


