 |
Отношения порядка. Диаграмма Хассе
|
|
|
|
Отношение эквивалентности является обобщением отношения равенства: эквивалентные элементы считаются «равными». Обобщением обычного отношения  служат отношения порядка.
служат отношения порядка.
Отношение  называется предпорядком или квазипорядком, если R рефлексивно и транзитивно.
называется предпорядком или квазипорядком, если R рефлексивно и транзитивно.
Пример. Отношение
R ={(1,1),(2,2),(3,3),(1,2),(2,1),(2,3),(1,3)}
на множестве X ={1,2,3} является предпорядком.
Рефлексивное, антисимметричное, транзитивное отношение называется отношением нестрогого порядка и обозначается символом  .
.
Антирефлексивное, антисимметричное, транзитивное отношение называется отношением строгого порядка и обозначается символом  . Отношения строгого и нестрогого порядков иначе называют отношениями упорядоченности. Отношение, обратное отношению упорядоченности, также является отношением упорядоченности, т.е. (
. Отношения строгого и нестрогого порядков иначе называют отношениями упорядоченности. Отношение, обратное отношению упорядоченности, также является отношением упорядоченности, т.е. ( )
)  =
=  .
.
Примеры:
1. Пусть Y – некоторое множество, тогда отношение включения 


 на множестве всех подмножеств P (Y) является отношением нестрогого порядка.
на множестве всех подмножеств P (Y) является отношением нестрогого порядка.
2. Отношение «х старше у» на некотором множестве людей является отношением строгого порядка.
Множество Х с заданным в нем отношением порядка называется упорядоченным этим отношением. Если любые два элемента х и у множества Х находятся между собой в отношении порядка, то множество Х называется линейно упорядоченным или цепью, иначе множество Х называется частично упорядоченным. В частично упорядоченном множестве можно выделить цепь. Цепь с повторяющимися элементами называется мультицепью. Если между элементами х и у установлено отношение порядка, то они называются сравнимыми, иначе – несравнимыми. Антицепью (семейством Шпернера) называется подмножество частично упорядоченного множества, в котором любые два элемента несравнимы. Специальным типом частично упорядоченного множества является интервал |x,y]={z  X|x
X|x  z
z  у} (замкнутый) или (x,y)P={z
у} (замкнутый) или (x,y)P={z  X|x
X|x  z
z  у} (открытый).
у} (открытый).
|
|
|
Двойственным к частично упорядоченному множеству называется частично упорядоченное множество, определенное на том же носителе с помощью обратного отношения. Это понятие лежит в основе принципа двойственности, который часто формулируют в виде: если некоторое утверждение справедливо для частично упорядоченных множеств, то справедливо и двойственное утверждение, то есть утверждение, касающееся двойственных частично упорядоченных множеств.
Рассмотрим множество Х с заданным на нем отношением частичного порядка  .
.
Говорят, что элемент y покрывает элемент x, если х  у и не существует никакого элемента z
у и не существует никакого элемента z  X, такого что х
X, такого что х  z
z  у. Таким образом, у покрывает х тогда и только тогда, когда х
у. Таким образом, у покрывает х тогда и только тогда, когда х  у и [ х,у ]={ х,у }. Любое частично упорядоченное множество можно представить в виде схемы. Диаграммой Хассе частично упорядоченного множества Х называется граф, вершинами которого являются элементы множества X, а пара (х,у) образует ребро, если элемент у покрывает элемент х, и такой что, если х
у и [ х,у ]={ х,у }. Любое частично упорядоченное множество можно представить в виде схемы. Диаграммой Хассе частично упорядоченного множества Х называется граф, вершинами которого являются элементы множества X, а пара (х,у) образует ребро, если элемент у покрывает элемент х, и такой что, если х  у, то у рисуют с большей вертикальной координатой чем х.
у, то у рисуют с большей вертикальной координатой чем х.
Пример. Отношение включения  на булеане Р (Х), где Х ={ а, b, с }. Оно является частично упорядоченным множеством. Множество Р (Х) содержит восемь элементов: {
на булеане Р (Х), где Х ={ а, b, с }. Оно является частично упорядоченным множеством. Множество Р (Х) содержит восемь элементов: {  , { a }, { b }, { c }, { a, b }, { a, c }, { b, c }, { a, b, c }}. Диаграмма Хассе для этого отношения будет иметь вид (рис. 2.2).
, { a }, { b }, { c }, { a, b }, { a, c }, { b, c }, { a, b, c }}. Диаграмма Хассе для этого отношения будет иметь вид (рис. 2.2). 
Рис. 2.2
Правило чтения диаграмм Хассе состоит в том, что х  у, если можно пройти из точки х в точку у, следуя вдоль восходящих отрезков соединяющих точки. Смена направления движения разрешается только в точках диаграммы.
у, если можно пройти из точки х в точку у, следуя вдоль восходящих отрезков соединяющих точки. Смена направления движения разрешается только в точках диаграммы.
Пример. Пусть А={1, 2, 3, 5, 6, 10, 15, 30}. Рассмотрим отношение частичного порядка ≤ на этом множестве, задаваемое по правилу: x ≤ y  y делится на x. Диаграмма Хассе изображена на рис.2.3.
y делится на x. Диаграмма Хассе изображена на рис.2.3.
|
|
|
Заметим, что диаграммы Хассе этих двух отношений совпадают
Пусть Х и Y два частично упорядоченных множества. Если их диаграммы Хассе совпадают, то эти частично упорядоченные множества имеют одинаковую структуру.
 Пример. На рис. 2.4 изображена диаграмма Хассе линейно упорядоченного множества Х={1, 2, 3, 4, 5, 6, 7, 8} с обычным отношением порядка (≤) на множестве натуральных чисел, не превосходящих восьми.
Пример. На рис. 2.4 изображена диаграмма Хассе линейно упорядоченного множества Х={1, 2, 3, 4, 5, 6, 7, 8} с обычным отношением порядка (≤) на множестве натуральных чисел, не превосходящих восьми.
Рис. 2.3 Рис. 2.4
Пусть задано частично упорядоченное множество X. Для элементов х и у из множества Х их верхней гранью называется любой элемент z  Х такой, что
Х такой, что 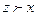 и
и  , а их нижней гранью – любой элемент t
, а их нижней гранью – любой элемент t  X, такой, что
X, такой, что 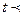 х и t
х и t  у. На языке диаграмм Хассе х
у. На языке диаграмм Хассе х  у означает, что существует путь из x в y; верхняя грань x и y – это вершина, в которую есть путь из x и y; нижняя грань x и y – это вершина из которой есть путь и в x и в y. В общем случае для некоторых элементов верхняя и нижняя грань может не существовать или быть неединственной, причем различные верхние (или нижние) грани могут быть несравнимы.
у означает, что существует путь из x в y; верхняя грань x и y – это вершина, в которую есть путь из x и y; нижняя грань x и y – это вершина из которой есть путь и в x и в y. В общем случае для некоторых элементов верхняя и нижняя грань может не существовать или быть неединственной, причем различные верхние (или нижние) грани могут быть несравнимы.
Пример. На рис. 2.5 а) изображена диаграмма Хассе множества 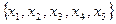 , у которого элементы
, у которого элементы  не имеют верхней грани, а элементы
не имеют верхней грани, а элементы  – нижней грани. На рис. 2.5 б) изображена диаграмма Хассе множества
– нижней грани. На рис. 2.5 б) изображена диаграмма Хассе множества  у которого все элементы имеют верхние и нижние грани, однако, например,
у которого все элементы имеют верхние и нижние грани, однако, например,  и
и  имеют две несравнимые верхние грани.
имеют две несравнимые верхние грани.
 |
Рис. 2.5
Задачи и упражнения
1. Даны множества Х 0={1,2,3,4,5,6}, X 1={1,2,3,4}, X 2={2,3,4,5}, X 3={2,3,4}, X 4={3,4,5}, X 5={2,3}, X 6={3,4}, X 7={4,5}, X 8={2,4}. Сформируйте частичный порядок на этих множествах.
2. Пусть Х - множество всех прямых на плоскости. Являются ли эквивалентными отношения а) параллельности прямых и б) перпендикулярности прямых?
3. Приведите пример четырех различных рефлексивных отношений на множестве  .
.
4. Приведите пример трех различных отношений на множестве  , не являющихся рефлексивными.
, не являющихся рефлексивными.
5. Приведите пример двух различных симметричных отношений и двух различных, не являющихся симметричными, на множестве 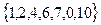 .
.
6. Приведите пример двух различных транзитивных отношений и двух различных, не являющихся транзитивными, на множестве 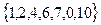 .
.
7. Приведите пример частичного порядка и пример отношения, не являющегося частичным порядком.
|
|
|
8. Приведите пример множества и двух различных эквивалентностей на нем.
9. Приведите пример множества и двух различных частичных порядков на нем.
10. Определите свойства следующих отношений, заданных на множестве действительных чисел (R)
а) R ={(x, y)| x, y Î R и x - y <0},
в) R ={(x, y)| x, y Î R и 2 x ³3 y },
с) R ={(x, y)| x, y Î R и | x | ³| y |}.
11. Найдите  ,
,  ,
,  ,
,  для отношений
для отношений
а) R ={(x,y) | x,y Î N и x, делит y },
в) R ={(x, y)| x, y Î R и x + y <0},
с) R ={(x, y)| x, y Î R и 2 x ³3 y }.
12. Докажите, что если отношения R 1 и R 2 рефлексивны, то рефлексивны следующие отношения  ,
,  ,
,  ,
, 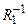 .
.
13. Докажите, что если отношения R 1 и R 2 симметричны, то симметричны следующие отношения  ,
,  ,
,  ,
, 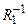 .
.
14. Докажите, что если R эквивалентность, то  есть также эквивалентность.
есть также эквивалентность.
15. Докажите, что  – эквивалентность тогда и только тогда, когда
– эквивалентность тогда и только тогда, когда  .
.
16. Для отношения, заданного матрицей, определить является ли оно отношением эквивалентности. Если является, то определить классы эквивалентности.
| а) | R | а | b | с | d | е | f | б) | R | а | b | с | d | е | f |
| а | а | ||||||||||||||
| b | b | ||||||||||||||
| с | с | ||||||||||||||
| d | d | ||||||||||||||
| е | е | ||||||||||||||
| f | f |
|
|
|


