 |
Матрица М данного графа имеет вид
|
|
|
|
 |
a b c d e f
1 b c a c c a
2 - e d f d b
3 - - - - - c
В качестве отправной вершины рассмотрим а. Множество S формируется следующим образом:
| Но-мер | Множество S | Комментарии |
| a | Добавляем первую возможную вершину в столбце а (т.е. вершину b). | |
| а,b | Добавляем первую возможную вершину в столбце b (т.е. вершину с) | |
| a,b,c | Первая вершина а в столбце с не является возможной (а Î S), добавляем следующую вершину в столбце (т.е. вершину d). | |
| a,b,c,d | Добавляем вершину f. | |
| a,b,c,d,f | В столбце f нет возможной вершины. Возвращение. | |
| a,b,c,d | В столбце d не существует возможной вершины, следующей за f. Возвращение. | |
| a,b,c | Аналогично предыдущему. Возвращение. | |
| а,b | Добавляем вершину е. | |
| a,b,e | Добавляем вершину с. | |
| a,b,e,c | Добавляем вершину d. | |
| a,b,e,c,d | Добавляем вершину f. | |
| a,b,e,c,d,f | Гамильтонов путь. Дуга (f,a) дает гамильтонов контур. Возвращение. | |
| a,b,e,c,d | Возвращение. | |
| a,b,e,c | Возвращение. | |
| a,b,e | Добавляем вершину d. | |
| a,b,e,d | Добавляем вершину f. | |
| a,b,e,d,f | Добавляем вершину c. | |
| a,b,e,d,f,c | Гамильтонов путь. Путь замыкается дугой (c,a). Возвращение. | |
| a,b,e,d,f | Возвращение. | |
| a,b,e,d | Возвращение. | |
| a,b,e | Возвращение. | |
| а,b | Возвращение. | |
| a | Возвращение. | |
| Æ | Конец поиска. |
В результате работы алгоритма определены гамильтоновы пути m1=[ a,b,e,c,d,f ], m2=[ a,b,e,d,f,c ] и контуры [ a,b,e,c,d,f,a ], [ a,b,e,d,f,c,a ].
Алгебраический метод выделения
Гамильтоновых путей и контуров
Замечание. «Внутреннее произведение вершин» пути [ x1,…,xk ] определяется как формальное выражение вида x2×x3×…xk-1, не содержащее две концевые вершины x1 и xk.
Шаг 1. G – данный орграф на n вершинах; А – матрица смежности с нулевыми элементами на диагонали; 
– модифицированная матрица смежности, в которой bij = b(ij)= xj, если существует дуга из xi в xj и 0 в противном случае. Положить k =1, R k= A.
|
|
|
Шаг 2. Положить k = k +1. Найти P k= B ´ P k-1.
Шаг 3. Если k = n, то диагональные элементы матрицы P n дают внутренние произведения вершин, которые соответствуют гамильтоновым контурам графа. Получить гамильтоновы контуры. Останов. Иначе перейти к шагу 4.
Шаг 4. Сделать все пути простыми, обнулив в матрице Pk все диагональные элементы, которые содержат сомножителями вершины, соответствующие данной строке. Перейти к шагу 5.
Шаг 5. Если k = n -1, то элементы матрицы Pk дают внутренние произведения вершин, которые соответствуют гамильтоновым путям графа G. Получить гамильтоновы пути. Перейти к шагу 2.
 |
Пример.Рассмотрим граф, изображенный на рис. 4.44.
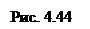
Матрица смежности А этого графа имеет вид
a b c d e
a 0 1 0 1 0
A = b 0 0 0 1 1
c 0 1 0 0 1
d 0 0 1 0 0
e 1 0 1 0 0
а модифицированная матрица смежности В выглядит следующим образом:
a b c d e
a 0 b 0 d 0
b 0 0 0 d e
B = c 0 b 0 0 e
d 0 0 c 0 0
e a 0 c 0 0
Положим P1 = A. Матрица P 2’= B × R 1 получается равной
a b c d e
a 0 0 d b b
b e 0 d+e 0 0
P2 ’ = c e 0 e b b
d 0 c 0 0 c
e 0 a+c 0 a c
Матрица P2 почти такая же, как P2 ’, только подчеркнутые элементы в P2 ’надо заменить нулями. Матрица P3 ’= B×P 2 равна
a b c d e
a be dc bd+be 0 dc
b 0 dc+ea+ec 0 ea dc
P3’= c be ea+ ecbd+be ea 0
d ce 0 0 cb cb
e ce 0 ad ab+cb ab+cb
Матрица Р 3 получается из P 3’ после замены подчеркнутых элементов нулями. Матрица Р 4’= B × P 3
a b c d e
a dce 0 0 bea bdc+dcb
b dce 0 ead eab+ecbdcb
P4’= c 0 0 ead bea+eab+ ecbbdc
d cbe cea 0 cea 0
e cbe adc+ cea abd+ abeceaadc
Гамильтоновы пути можно определить по матрице Р 4, которая имеет вид
a b c d e
a 0 0 0 0 bdc+cdb
b dce 0 ead 0 0
P4= c 0 0 0 bea+eab 0
d cbe cea 0 0 0
e 0 adc abd 0 0
Гамильтоновы пути abdce и adcbe, соответствующие элементу (1,5) матрицы Р 4 дают гамильтоновы контуры abdcea и adcbea, если добавить замыкающую дугу (е,а). Все другие гамильтоновы пути в Р 4 приводят к тем же самым контурам, и потому в графе G есть только два таких контура.
|
|
|
|
|
|
