Алгоритм укладки графа на плоскости

 

Рассмотрим граф G =(X, V). Алгоритм укладки графа представляет собой процесс последовательного присоединения к некоторому уложенному подграфу G ' (G' =(X', V')) графа G новой цепи, оба конца которой принадлежат G'. Тем самым эта цепь разбивает одну из граней G' на две. При этом в качестве начального плоского графа G' выбирается любой простой цикл графа G. Процесс продолжается до тех пор, пока не будет построен плоский граф, изоморфный графу G, или присоединение некоторой цепи окажется невозможным. В этом случае граф не является планарным.

Введем ряд определений.

Пусть построена некоторая укладка подграфа G' графа G. Сегментом S относительно G' (или просто сегментом) будем называть подграф графа G одного из следующих двух видов:

1) ребро v =(x, y) G, такое, что v Ï G', x, y Î X';

2) связанную компоненту графа G \ G', дополненную всеми ребрами графа G, инцидентными вершинам взятой компоненты, и концами этих ребер.

Очевидно, что в случае, когда граф G планарный, всякий сегмент, как подграф графа G, планарен, а в случае, когда G не является планарным, сегмент может быть как планарным, так и не планарным.

Вершину x сегмента S относительно G' будем называть контактной, если x Î X'.

Поскольку граф G' плоский, то он разбивает плоскость на грани. Допустимой гранью для сегмента S относительно G' называется грань Г графа G', содержащая все контактные вершины сегмента S. Через Г (S) будем обозначать множество допустимых граней для S. Может оказаться, что Г (S)=Æ.

Простую цепь L сегмента S, соединяющую две различные контактные вершины и не содержащую других контактных вершин, назовем a –цепью. Очевидно, что всякая a –цепь, принадлежащая сегменту, может быть уложена в любую грань, допустимую для этого сегмента.

Два сегмента S₁ и S₂ относительно G' назовем конфликтующими, если

1) D = Г (S₁)Ç Г (S₂)¹Æ,

2) существуют две a -цепи L₁ Î S_{1 ,} L₂ Î S₂, которые без пересечений нельзя уложить одновременно ни в какую грань Г Î D. В противном случае будем говорить, что сегменты не конфликтуют.

Вернемся к алгоритму. На первом шаге этого алгоритма уложим произвольный простой цикл графа G.

Пусть G' – построенная на предыдущем шаге укладка некоторого подграфа графа G. Для каждого сегмента относительно G' находим множество допустимых граней. Теперь могут представиться только следующие три случая.

1. Существует сегмент, для которого нет допустимой грани. В этом случае граф не планарен.

2. Для некоторого сегмента S существует единственная допустимая грань Г. Тогда очередной шаг состоит в расположении любой a –цепи сегмента S в грани Г. При этом a –цепь разбивает грань Г на две грани.

3. для всякого сегмента S. Тогда появляется несколько вариантов продолжения построения укладки графа, поскольку любой сегмент можно размещать в любую допустимую для этого сегмента грань. Поэтому возникают опасения, что неудачный выбор сегмента и грани может помешать процессу построения укладки на следующих шагах и плоская укладка планарного графа не будет построена. Это могло бы привести к неверному заключению о том, что планарный граф непланарен. В [2] показано, что в этом случае для продолжения алгоритма можно выбирать a –цепь в любом сегменте и помещать его в любую допустимую грань.

Опишем пошагово алгоритм укладки графа на плоскости.

Шаг 1. Выберем некоторый простой цикл С графа G и уложим его на плоскости. Положим G' = С.

Шаг 2. Найдем грани графа G' и сегменты относительно G'. Если множество сегментов пусто, то перейдем к шагу 8.

Шаг 3. Для каждого сегмента S определим множество Г (S).

Шаг 4. Если существует сегмент S, для которого Г (S)=Æ, то граф G непланарен. Конец. Иначе перейти к шагу 5.

Шаг 5. Если существует сегмент S, для которого имеется единственная допустимая грань Г, то перейти к шагу 7. Иначе – к шагу 6.

Шаг 6. Для некоторого сегмента S () выбираем произвольную допустимую грань Г.

Шаг 7. Поместить произвольную a –цепь L Î S в грань Г. Заменить G' на G' È L и перейти к шагу 2.

Шаг 8. Построена укладка G' графа G на плоскости. Конец.

Примеры. 1. Для графа G, изображенного на рис. 4.48, построить его уклад­ку на плоскости. Уложим сначала цикл С =(1, 2, 3, 4, 1), который разбивает плоскостьна две грани Г₁ в Г₂. На рис. 4.49 изображены граф G' = С и сегменты S₁, S₂, S₃ относительно G' с контактными вершинами, обведенными кружками. Таккак Г (S_i)={ Г₁, Г₂ } (i =1, 2, 3), то любую a -цепь произвольного сегмента можно укладывать в любую допустимую для него грань. Поместим, например, a -цепь L =(2, 5, 4) в Г₁. Возникает новый граф G' и его сегменты (рис. 4.50). При этом Г (S₁)={ Г₃ }, Г (S ₂)={ Г₁, Г₂ }, Г (S₃)={ Г ₁, Г ₂, Г ₃}. Укладываем цепь L =(1, 5) в Г₃ (рис. 4.51). Тогда Г (S ₁) = { Г ₁, Г ₂}, Г (S ₂)={ Г ₁, Г ₂}. Далее, уложим a -цепь L =(2, 6, 4) сегмента S₁ в Г₁ (рис. 4.52). В результате имеем Г (S ₁)={ Г ₅}, Г (S ₂) ={ Г ₁, Г ₂, Г ₃}. Наконец, уложив ребро (6,3) в Г ₅, а ребро (2,4) – например, а Г₁, получаем укладку графа G на плоскости (рис. 4.53).

1 2 3

 

6 5 4

 

Рис. 4.48

1 2 5 6 2

 

 

Г₂ Г₁

 

4 3 1 2 4 2 3 4 4

G' S₁ S₂ S₃

Рис. 4.49

1 2 5 6 2

 

 

Г₂ Г₃ Г₁

 

4 3 1 2 3 4 4

G' S₁ S₂ S₃

Рис. 4.50

1 2 6 2

Г₄

Г₂ Г₃ Г₁

 

4 3 2 3 4 4

G' S₁ S₂

Рис. 4.51

 

1 2 6 2

Г₄

Г₂ Г₃ Г₁

5 6

Г₅

4 3 3 4

G' S₁ S₂

Рис. 4.52

 

1 2

 

5 6

 

4 3

G' Рис. 4.53

 

2. Для графа К _3,3, изображенного на рис.4.54, построить, если это возможно, его уклад­ку на плоскости. Цикл G' и сегменты относительно этого цикла изображены на рис. 4.55. При этом Г (S_i) = { Г _1, Г ₂} (i =1,2,3). Помещает S₁ в грань Г₂. Тогда S₂ необходимо поместить в грань Г₁ (рис. 4.56). Поскольку Г (S₁)=Æ, то К _3,3 – непланарный граф.

 

1 2 3

 

6 5 4

Рис. 4.54

 

1 6 3 1 2 3

 

 

Г₁ Г₂

 

 

5 2 4 4 6 5

G' S₁ S₂ S₂

Рис. 4.55

 

1 6 3 3

 

 

5 2 4 5

G' S₁

Рис. 4.56

 

Задачи и упражнения

 

1. Доказать, что в неорграфе число вершин с нечетной степенью четно.

2. Построить граф (если он существует) с последовательностью степеней

а) (4,3,3,2,2);

б) (5,4,2,2,1).

3. Найти матрицы достижимости и контрдостижимости для графов G₁, G₂, G₄, изображенных на рис. 4.57.

 

 

Рис. 4.57

 

4. Доказать, что если в n -вершинном графе степень каждой вершины не меньше, чем (n -1)/2, то он связен.

5. Доказать, что если G - несвязный граф, то ` G - связный.

6. Доказать, что в любом графе каждая его база содержит все вершины, имеющие нулевые полустепени захода.

7. Для графов, изображенных на рис. 4.58, найти сильнее компоненты, построить конденсацию, найти базы и антибазы.

 

Рис. 4.58

 

8. Доказать, что хроматическое число каждого n -вершинного дерева (n ³2) равно 2.

9. Построить остовы для графов, изображенных на рис. 4.59.

Рис. 4.59

 

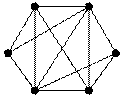
10. Существует ли эйлеров цикл в графах, изображенных на рис. 4.60?

 

Рис. 4.60

 

11. Определить, какие из графов пяти правильных многогранников имеют эйлеровы циклы.

12. Составить алгоритм, основанный на алгоритме Флери и позволяющий найти все эйлеровы циклы графа.

13. Определить гамильтоновы пути и контуры методом перебора Робертса и Флореса в графах, изображенных на рис. 4.61.

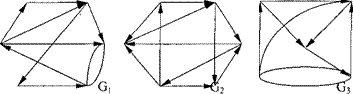Рис. 4.61

14. Для графа построить, если это возможно, его уклад­ку на плоскости.

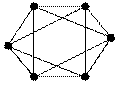
а) б)

 

 

д) е)

АЛГЕБРА ЛОГИКИ

Под высказыванием понимают повествовательное предложение, относительно которого имеет смысл утверждать, истинно оно (обозначается символами 1 или И) или ложно (символы 0 или Л). Значения И и Л (или 1 и 0) называются истинностными значениями высказывания, множество {И, Л} (или {0,1}) называется множеством истинностных значений. Заметим, что значение высказывания ситуативно, при этом в каждой ситуации высказывание принимает одно и только одно из двух значений – И или Л.

Например, повествовательное предложение «3 есть простое число» является истинным, а «3.14… – рациональное число» – ложным, «Колумб открыл Америку» – истинным, а «Киев – столица Узбекистана» – ложным, «Число 6 делится на 3» – истинным, а «Сумма чисел 2 и 3 равна 6» – ложным и т. п.

Такие высказывания называют простыми или элементарными. При формальном исследовании сложных текстов вместо понятия «простые высказывания» используют понятие «пропозициональные переменные» (от лат. propositio – предложение), которые обозначают прописными буквами латин­ского алфавита A, B, C,… Истинность или ложность высказывания будем отмечать символами 1 – истина или 0 – ложь.

Пример:

1) если A₁ =«5 – простое число», то A₁ = 1;

2) если A₂ =«2 – вещественное число», то A₂ = 1;

3) если B₁ =«3, 14…– рациональное число», то B₁ = 0;

4) если D =«Сумма чисел 2 и 3 равна 6», то D = 0.

Замечание. Символ «=» означает, что пропозициональной переменной, стоящей слева, присвоить значение высказывания, стоящего справа от символа.

Правила построения сложных высказываний в виде последователь­ности пропозициональных переменных, логических связок и вспомогательных символов определяют возможность формального описания любого текста. При формальной записи сложного высказывания всегда нужно исходить из его содержания. До тех пор пока не определена логическая структура сложного высказывания, его нельзя формально описывать.

Правила выполнения логических операций над сложными высказываниями на основе заданных логических связок и пропозициональных переменных формирует алгебру высказываний.

 

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: