 |
Пример. Математическая постановка задачи нахождения оптимальной последовательности выпуска изделий.
|
|
|
|
Введем некоторые обозначения. Пусть {a1…aL} - множество всевозможных последовательностей выпуска изделия L модификаций;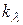 
- количество оборудования в группе 
, где =1,…, N;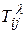 
- время, необходимое на переналадку единицы оборудования -ой группы при переходе с выпуска i -ой модификации на выпуск j -ой модификации.
Пусть G - ориентированный граф, вершины которого представляют изделия, а существование дуги (хi, хi) означает, что изделие j может следовать за изделием i без перенастройки оборудования. Тогда, если в этом графе есть гамильтонов цикл (ориентированный цикл, проходящий через каждую вершину графа), то существует последовательность выпуска изделий, не требующая перенастройки оборудования. Если не существует циклической последовательности выпуска изделий, не требующей перенастройки оборудования, то задача сводится к нахождению последовательности выпуска изделий, требующих наименьших затрат на перенастройку оборудования.
Пусть хij =1, если после изделия i -ой модификации выпускается изделие j -ой модификации; хij =0, если после изделия i -ой модификации изделие j -ой модификации не выпускается.
С так введенными переменными ставим задачу:
Минимизировать функцию
(1)
при условиях
, 
, 
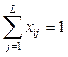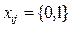. (2)
В качестве дополнительных ограничений необходимо наложить условие «петель», для устранения подконтуров в задаче
(3)
Задача (1)-(3) полностью аналогична классической задаче коммивояжера:
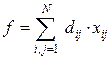(4)
при условиях
, 
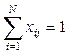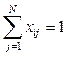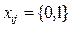, . (5)
условие «петель»
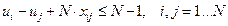(6)
В задаче коммивояжера (4)-(6) ищется оптимальная последовательность обхода «городов», а в задаче (1)-(3) оптимальная последовательность выпуска изделий. В задаче (4)-(6) матрица D с элементами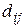 
является матрица расстояний между N «городами», этой матрице соответствует матрица В в задаче (1)-(3) с элементами 
, которая является матрицей времени переналадки оборудования
|
|
|
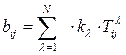
Таким образом, задачу оптимизации последовательности выпуска изделий можно решить методами решения задачи коммивояжера.
4.13. Плоские и планарные графы
Во многих случаях не имеет значения, как изобразить граф, поскольку изоморфные графы несут одну и ту же информацию. Однако встречаются ситуации, когда важно выяснить, возможно ли нарисовать граф на плоскости так, чтобы его изображение удовлетворяло определенным требованиям.
Плоским графом называется граф, вершины которого являются точками плоскости, а ребра – непрерывными линиями без самопересечений, соединяющими соответствующие вершины так, что никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины.
 |
Примеры плоских графов (рис. 4.45).
 |
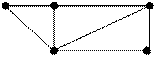А б
Рис. 4.45. Плоские графы
Любой граф, изоморфный плоскому графу, будем называть планарным. Граф на рис. 4.46 является планарным, так как он изоморфен графу на рис. 4.45.б.
 |
Рис.4.46
Очевидны следующие утверждения:
1) всякий подграф планарного графа планарен;
2) граф планарен тогда и только тогда, когда каждая его связная компонента – планарный граф.
О планарных графах говорят, что они укладываются на плоскости (имеют плоскую укладку).
Формула Эйлера
Область, ограниченная ребрами в плоском графе, и не содержащая внутри себя вершин и ребер, называется гранью графа. Внешняя часть плоскости также образует грань. На рис. 4.47 изображен граф с 3 гранями.
Будем использовать следующие обозначения: n, m, f – соответственно число вершин, ребер и граней плоского графа.
 |
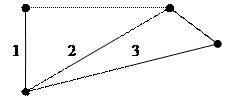Рис. 4.47
Теорема 4.13.1. (Теорема Эйлера, 1758 г.). Для всякого связного плоского графа верно равенство
n – m + f =2, (4.6)
которое называется формулой Эйлера.
|
|
|
Доказательство. G – связный плоских n -вершинный граф. Рассмотрим некоторый остов Т этого графа. Очевидно, что дерево Т имеет одну грань (внешнюю) и n вершин. В то же время известно, что число ребер дерева Т равно n –1. Поэтому для графа Т формула (4.6) верна. Теперь будем поочередно добавлять к Т недостающие ребра графа G. При этом на каждом шаге число вершин не меняется, а число ребер и число граней увеличивается на единицу. Следовательно формула (4.6) будет верна для всякого графа, получающегося в результате таких операций, а потому она верна и для графа G, которым заканчивается вся эта процедура.
Из теоремы Эйлера вытекают следующие следствия.
Следствие 4.13.1. Число граней любой плоской укладки связного планарного графа постоянно и равно m – n +2.
Другими словами, число f не зависит от способа укладки этого графа на плоскости.
Следствие 4.13.2. Для связного планарного графа m £3 n -6 при n ³3.
Формула Эйлера позволяет доказать непланарность некоторых графов.
Графом K 5 называется граф с 5 вершинами, в котором каждая пара вершин соединена ребром.
Теорема 4.13.2. Граф K 5 не планарен.
Доказательство. Допустим, что для графа K 5 существует планарная реализация. Так как граф K 5 связен, то для этой планарной реализации справедлива формула Эйлера n – m + f =2. Поскольку в графе K 5 имеем n =5 и m =10, то число всех граней должно равняться f =2– n + m =7. Пусть грани занумерованы 1, 2,..., f и пусть при обходе i -ой грани по периметру (по ее краю) проходится mi ребер. Так как при этом каждое ребро проходится дважды (оно является стороной для двух граней), то 
. Но в каждой грани не менее 3 сторон. Поэтому m i³3 для всех i. Отсюда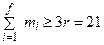 
. Получаем 20 ³ 21 – противоречие. Значит, для графа K 5 не существует планарной реализации.
Графом K 3,3 называется граф с 6 вершинами a 1, a 2, a 3, b 1, b 2, b 3, в котором каждая вершина a i соединена ребром с каждой вершиной b j и нет других ребер.
С графом K 3,3 связана следующая известная задача о трех домах и трех колодцах. Есть 3 дома и 3 колодца, но хозяева домов в большой вражде. Можно ли так проложить дорожки от каждого дома к каждому колодцу, чтобы они нигде не пересекались? Ответ на этот вопрос дает следующая теорема.
Теорема 4.13.3. Граф K 3,3 не планарен.
Доказательство. Допустим, что для графа K 3,3 существует планарная реализация. Так как граф K 3,3 связен, то для этой планарной реализации справедлива формула Эйлера n – m + f = 2. Поскольку в графе K 3,3 имеем n =6 и m =9, то число всех граней должно равняться f =2– n + m =5. Так же, как в доказательстве предыдущей теоремы, получаем, что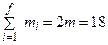 
, где m i - число сторон в i -ой грани. Но в графе K 3,3 нет циклов длины 3. Поэтому в каждой грани не менее 4 сторон. Следовательно, m i³4 для всех i. Отсюда 
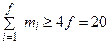. Получаем 18 ³ 20 - противоречие. Значит, для графа K 3,3 не существует планарной реализации.
|
|
|
4.13.2. Критерии анализа планарности
Граф G 1 называется подразбиением графа G, если G 1 может быть получен из G несколькими подразбиениями ребер.
Графы G 1 и G 2 называются гомеоморфными, если оба они могут быть получены из одного и того же графа подразбиением его ребер.
Существует следующий критерий планарности.
Теорема 4.13.4. (Понтрягина-Куратовского). Для того чтобы граф G был планарным, необходимо и достаточно, чтобы он не содержал ни одного подграфа, гомеоморфного графам K 5 или K 3,3.
Эквивалентная форма критерия планарности описана в следующей теореме.
Теорема 4.13.5. (К. Вагнер, 1937 г.). Граф планарен тогда и только тогда, когда в нем нет подграфов, стягиваемых к графам К 5 или К 3,3.
Под стягиванием понимается последовательное отождествление вершин, связанных ребрами.
Рассмотренные критерии планарности таковы, что если даже удалось установить планарность графа, то нет информации о том, как строить его укладку на плоскости. В то же время для решения практических задач недостаточно знать, что граф планарен, а необходимо построить его плоское изображение. Появились алгоритмы, которые не только проверяют граф на планарность, но и одновременно строят его плоскую укладку, если это возможно. Одним из таких алгоритмов является следующий [1].
|
|
|
