 |
Правила записи сложных формул
|
|
|
|
При записи сложных высказываний следует обращать внимание, чтобы в формулах не было двух рядом стоящих логичеcких операций. Они должны быть разъединены формулами либо вспомогательными символами.
При записи сложных формул следует помнить, что
1) каждое вхождение логической связки 
относится к пропозициональной переменной или формуле, следующей непосредственно за логической операцией справа;
2) каждое вхождение логической операции Ù после расстановки скобок связывает пропозициональные переменные или формулы, непосредственно окружающие логическую операцию;
3) каждое вхождение логической операции Ú после расстановки скобок связывает пропозициональные переменные или формулы, непосредственно окружающие эту операцию и т.д.
При использовании этих правил к одной и той же формуле скобки следует расставлять постепенно, продвигаясь слева направо.
Пример. Пусть дана формула
F =((X 1Ú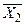 
)® X 3)«X 4.
Последовательность выполнения операций после задания значений пропозициональных переменных следующая: сначала необходимо определить значение формулы 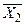, затем (X 1Ú 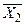) затем (X 1Ú 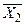)® X 3) и, наконец,
((X 1Ú 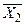)® X 3)«X 4.
Пример. Для формулы F = X 1Ù X 2Ù X 3Ú 
® X 3«X 1. последовательность выполнения логических операций следующая: операций 
.
Таблицы истинности
Каждая пропозициональная переменная принимает значения 0 или 1, тогда ПФ в соответствии с определением логических операций также принимает значения 0 или 1, поэтому ее можно рассматривать как функцию, область значений и область определения которой совпадают и равны {0,1}. Такую функцию будем называть булевой функцией, двоичной или переключательной функцией.
|
|
|
Каждой ПФ, а значит и булевой функции, можно поставить в соответствие таблицу, называемую таблицей истинности, в которой перечислены все возможные значения входящих в нее переменных и значения ПФ или булевой функции на этих наборах. Каждый такой набор можно рассматривать как запись некоторого n -разрядного двоичного числа, при этом наибольшее двоичное число получим, составив набор из одних 1, а наименьшее – из одних 0. Таким образом, наибольшему числу соответствует десятичное число 
– 1, а наименьшему – 0; всем остальным возможным наборам числа, заключенные между 0 и –1. Это соответствие способствует упорядочению наборов аргументов булевой функции, которые заносятся в таблицу в порядке возрастания. Если функция зависит от n переменных, то таблица истинности содержит наборов значений переменных.
С помощью таблицы истинности определяются все логические операции над высказываниями:
| X | Y | 
| 
| 
| 
| 
| 
|
Пример. Рассуждение «если инвестиции на текущий год не изменятся (A), то возрастет расходная часть бюджета (B) или возникнет безработица (C), а если возрастет расходная часть бюджета, то налоги не будут снижены (D) и, наконец, если налоги не будут снижены и инвестиции не изменятся, то безработица не возникнет».
В этом рассуждении есть четыре повествовательных предложения, которые следует заменить пропозициональными переменными и формально описать суждение. Тогда формула сложного рассуждения имеет вид:
F =(A ®(B Ú C)) Ù (B ® D) Ù ((D Ù A)® 
).
Для различных значений истинности пропозициональных переменных и подформул, построенных на логических операциях, можно последовательно определить значение истинности формулы F. Ниже представлена таблица истинности для этого рассуждения.
|
|
|
Для удобства записи любой подформулы и формулы каждый столбец пронумерован и логические операции выполняются с индексами столбцов.
| A | B | C | D | ùC | 4Ù1 | 2Ú3 | 1®7 | 2®4 | 6®5 | 8Ù9 | 11Ù10 |
Пример. Составим таблицу истинности для высказывания: «На экзамене я получу оценку «хорошо» или «отлично»». Выделим два простых высказывания: высказывание X = «На экзамене я получу оценку «хорошо»» и высказывание Y = «На экзамене я получу оценку «отлично»». Таблица истинности примет вид
| X | Y | X или Y |
По таблице истинности сложное высказывание «X или Y» можно представить как формулу 
, которую называют отрицанием эквивалентности или операцией сложения по модулю 2 и обозначают 
.
ПФ называется тождественно истинной, общезначимой или тавтологией, если она принимает значение 1 на всех наборах значений переменных. Для обозначения того, что ПФ F есть тавтология используют запись ├ F.
ПФ называется тождественно ложной или противоречием, если она принимает значение 0 на всех наборах значений переменных.
ПФ называется выполнимой или опровержимой, если на некоторых наборах значений переменных она принимает значение 1, а на остальных – 0.
Тип ПФ можно определить с помощью таблицы истинности.
|
|
|
Пример. Определить тип ПФ 
. Для определения типа ПФ составим таблицу истинности
| X | Y | 
| 
| 
| 
|
Как видно из таблицы истинности, данная ПФ является тождественно ложной, так как принимает значение 0 на всех наборах переменных.
Равносильность формул
Различные формулы могут иметь одинаковые таблицы истинности. Так возникает понятие равносильности формул.
Две формулы алгебры высказываний F1 и F2 называются равносильными (эквивалентными), если их таблицы истинности совпадают. Равносильность формул будем обозначать через F1 ≡ F2. Нужно различать символы ↔ и ≡. Символ ↔ является символом формального языка, с помощью которого строятся формулы; символ ≡ заменяет слово «равносильно». Заметим, что отношение равносильности есть отношение эквивалентности. При этом справедливы утверждения:
1. Если две ПФ равносильны и одна из них содержит переменные, которых нет в другой, то ПФ от этих переменных не зависит (такие переменные называются фиктивными).
2. Если две ПФ равносильны, то их отрицания также равносильны.
3. Если в двух равносильных ПФ все вхождения некоторой переменной заменить любой формулой, то полученные новые ПФ будут равносильны.
Для любых формул X, Y, Z справедливы следующие равносильности (законы алгебры высказываний):
1. 
, 
(коммутативность);
2. 
, 
(ассоциативность);
3. 
, 
(дистрибутивность);
4. 
, 
(идемпотентность);
5. 
, 
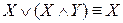(законы поглощения );
6. 
(закон двойного отрицания);
7. 
, 
(законы де Моргана);
8. 
, 
, 
, 
, 
, 
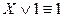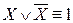(законы, определяющие действия с константами);
9. 
, 
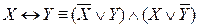(исключение импликации и эквиваленции);
10. 
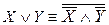(исключение дизъюнкции);
11. 
(исключение конъюнкции).
Любая равносильность может быть доказана либо с помощью таблиц истинности, либо равносильными преобразованиями. Докажем, например, равносильность для исключения импликации
.
Для этого составим таблицы истинности для ПФ, стоящих в левой и правой частях выражения, и сравним их.
|
|
|
| Х | Y |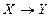 
| 
|
Пример.Доказать равносильность
Используя закон поглощения, дистрибутивный закон и закон, определяющий действие с 1, получим
Понятия «равносильность» и «тавтология» связаны между собой следующим образом.
Теорема. F 1≡ F 2 тогда и только тогда, когда F 1↔ F 2 является тавтологией.
Справедливость этой теоремы вытекает непосредственно из определений ≡ и тавтологии.
Пример. Доказать 
.
Покажем, что соответствующая эквиваленция является тавтологией.
 |
Знание законов алгебры высказываний позволяет выполнять равносильные преобразования любых логических формул, сохраняя их значения для любых наборов пропозициональных переменных. Ниже на примерах рассмотрены равносильные преобразования основных логических операций.
Пример. X ® Y º Ú Y = 
.
X «Y º(X ® Y) Ù (Y ® X) º ( Ú Y) Ù (
Ú X) 
.
То есть операцию эквиваленции всегда можно заместить операций импликации и конъюнкции или дизъюнкции и отрицания.
Пример. X «Y º Ù Ú X Ù Y º 
.
Выполненные примеры показывают, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей вместо импликации или эквиваленции только две логических операции: дизъюнкцию и отрицание или конъюнкцию и отрицание. Этот факт показывает, что множество логических связок дизъюнкции и отрицания, конъюнкции и отрицания формируют функционально полные алгебраические системы. Они достаточны для выражения любой логической функции
Если формула F содержит подформулу Fi, то замена подформулы Fi в формуле F на эквивалентную ей формулу Fj не изменяет значения формулы F при любом наборе пропозициональных переменных. Если необходима подстановка в формулу F вместо формулы Fi новой формулы Fj, то эту операцию нужно выполнить всюду по символу Fi.
Правила замены и подстановки расширяют возможности эквивалентных преобразований формул сложных высказываний.
Пример. Дано F =(X 1® X 2) ®((X 2® X 3) ®(X 1Ú X 2 ® X 3)).
Выполним преобразования для упрощения алгебраического выражения.
1) Удалим всюду логическую связку ®:
F =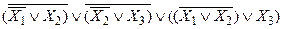 
;
2) Выполним преобразование по закону де Моргана:
F = X 1Ù 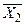Ú X 2Ù 
Ú Ù 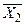Ú X 3;
3) Выполним преобразование по закону дистрибутивности:
F =(X 1Ú ) Ù 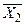Ú X 2 Ù Ú X 3;
4) Удалить (X 1Ú ), так как (X 1Ú )=1:
F = 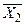Ú X 2Ù Ú X 3;
5) Выполним преобразование по закону дистрибутивности:
F = 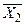Ú(X 2Ú X 3) Ù ( Ú X 3);
6) Удалим (X 3Ú )=1:
F = 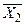Ú(X 2Ú X 3);
7) Применим закон ассоциативности:
F =(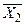 Ú X 2)Ú X 3;
7) Удалим (X 2Ú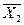 
), так как (X 2Ú 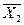)=1:
|
|
|
8) Получим
F =1Ú X 3=1.
Пример. Дано рассуждение «или верно, что Петр поступил в университет (А), и при этом неверно, что Петр не поступил и Андрей не поступил, или Петр поступил и Семен поступил (С), или даже Петр поступил и Семен поступил, и Андрей поступил (В)».
Формула сложного высказывания имеет вид:
А Ù 
Ú А Ù С Ú А Ù В Ù С;
1) преобразуем формулу, используя закон де Моргана, получим:
А Ù(А Ú В)Ú А Ù С Ú А Ù В Ù С;
2) применим закон идемпотентности:
А Ù(А Ú В)Ú A Ù А Ù С Ú А Ù В Ù С;
3) применить закон дистрибутивности по переменной А:
А Ù((А Ú В)Ú А Ù С Ú В Ù С);
4) применим закон дистрибутивности по переменной С:
А Ù((А Ú В)Ú С Ù (А Ú В));
5) введем константу 1:
А Ù((А Ú В) Ù1Ú С Ù (А Ú В));
6) применить закон дистрибутивности для подформулы (А Ú В), получим:
А Ù(А Ú В) Ù (1Ú С);
7) удалим (1Ú С), получим:
А Ù (А Ú В);
8) применить закон поглощения, получим:
А.
Следовательно, в данном высказывании утверждается только то, что Петр поступил в университет, а об Андрее и Семене никакой информации нет.
Пример. Шесть школьников – Андрей, Борис, Григорий, Дмитрий, Евгений и Семен – участвовали в олимпиаде. Двое из них решили все задачи. На вопрос, кто решил все задачи, последовали ответы: 1) Андрей и Дмитрий; 2) Борис и Евгений; 3) Евгений и Андрей; 4) Борис и Григорий; 5) Семен и Андрей. В четырех из этих ответов одна часть неверна, другая верна. В одном – обе части неверны. Кто решил все задачи?
Введем обозначения:
A= «Андрей решил все задачи»;
Б= «Борис решил все задачи»;
Г= «Григорий решил все задачи»;
Д= «Дмитрий решил все задачи»;
Е= «Евгений решил все задачи»;
С= «Семен решил все задачи».
Так как в одном из ответов обе части неверны, а в остальных – одна, то необходимо составить пять формул, отражающих пять различных высказываний:
Ù 
Ù (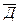
Ù Е Ú Б Ù 
) Ù ( Ù А Ú Е Ù ) Ù ( Ù Г Ú Б Ù 
) Ù
Ù ( Ù А Ú С Ù );
Ù Ù ( Ù Д Ú А Ù ) Ù ( Ù А Ú Е Ù ) Ù ( Ù Г Ú Б Ù ) Ù
Ù ( Ù А Ú С Ù );
Ù Ù ( Ù Д Ú А Ù ) Ù ( Ù Е Ú Б Ù ) Ù ( Ù Г Ú Б Ù ) Ù
Ù ( Ù А Ú С Ù );
Ù Ù ( Ù Д Ú А Ù ) Ù ( Ù Е Ú Б Ù ) Ù ( Ù А Ú Е Ù ) Ù
Ù ( Ù А Ú С Ù );
Ù Ù ( Ù Д Ú А Ù ) Ù ( Ù Е Ú Б Ù ) Ù ( Ù А Ú Е Ù ) Ù
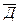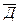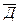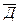Ù ( Ù Г Ú Б Ù ).
Если допустить, что º1 и 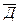º1, то первая формула может быть записана так:
Ù Ù 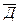( Ù Е Ú Б Ù ) Ù Е Ù Ù ( Ù Г Ú Б Ù ) Ù С Ù ,
т. к. член Ù А º0.
Если допустить, что º1 и º1, то вторая формула может быть записана так:
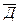Ù Ù ( Ù Д Ú А Ù ) Ù Ù А Ù Ù Г Ù ( Ù А Ú С Ù ),
т. к. члены Е Ù º0 и Б Ù º0.
Если допустить, что º1 и º1, то третья формула может быть записана так:
Ù Ù ÙДÙБÙ Ù ( ÙГÚБÙ )ÙСÙ ,
т. к. члены А Ù 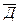º0, Ù Е =0, и Ù А º0.
Если допустить, что º1 и º1, то четвертая формула может быть записана так:
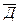Ù Ù( Ù Д Ú А Ù )Ù Ù Е Ù( Ù А Ú Е Ù )Ù( Ù А Ú С Ù ), т. к. член Б Ù º0.
Если допустить, что º1 и º1, то пятая формула может быть записана так:
Ù Ù Ù Д Ù ( Ù Е Ú Б Ù ) Ù Е Ù Ù ( Ù Г Ú Б Ù ),
т. к. член А Ù 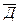º0.
Применив законы дистрибутивности, идемпотентности и поглощения эти формулы можно упростить так:
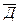Ù Ù Ù Е Ù Г Ù С;
Ù 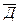Ù Ù Ù А Ù Г;
Ù Ù Ù Д Ù С Ù Б;
Ù Ù Ù Д Ù Е Ù С;
Ù Ù Ù Д Ù Е Ù Г.
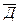По условиям задачи только два участника решили все задачи. Поэтому формулы, содержащие по три пропозициональных переменных без отрицания, не отвечают поставленным условиям, а одна, содержащая только две переменных без отрицания, отвечает условиям задачи. Это формула Ù Ù Ù Ù А Ù Г. Следовательно, все задачи на олимпиаде решили Андрей (А) и Григорий (Г).
|
|
|
