Операции над высказываниями

Условимся считать высказывание элементарным (простым), если никакую его часть нельзя рассматривать как отдельное высказывание. Для образования составных (сложных) высказываний используют логические связки (логические операции).

Пусть X и Y – два высказывания. Определим основные логические операции.

Отрицанием высказывания X называется высказывание , которое истинно тогда и только тогда, когда Х ложно. В разговорной речи высказывание соответствует составлению из высказывания Х нового высказывания «не Х» или «неверно, что Х». Для обозначения отрицания высказывания также используют запись Х (ù Х).

Конъюнкцией двух высказываний Х и Y называется высказывание Х Ù Y, которое истинно тогда и только тогда, когда истинны оба высказывания. Конъюнкция иначе называется логическим умножением, а Х и Y – сомножителями. В разговорной речи конъюнкция соответствует соединительному союзу «и», Х Ù Y – читается как «Х и Y». Для обозначения конъюнкции высказываний также используют запись Х & Y.

Дизъюнкцией двух высказываний Х и Y называется высказывание Х Ú Y, которое ложно тогда и только тогда, когда Х и Y ложны. Дизъюнкция иначе называется логическим сложением, а Х и Y – слагаемыми. В разговорной речи дизъюнкция соответствует соединительному союзу «или», Х Ú Y – читается как «Х или Y».

Замечание. Следует обратить внимание, что в повседневной речи союз «или» употребляется в двух смыслах: «исключающее или», когда истинность составного высказывания определяется истинностью только одного из высказываний, и «не исключающее или», когда истинность составного высказывания определяется истинностью хотя бы одного из высказываний. «Исключающее или» не является операций дизъюнкцией. Пример высказывания, в котором союз «или» не является операцией дизъюнкция, «На экзамене я получу оценку «хорошо» или «отлично»».

Импликацией двух высказываний Х и Y называется высказывание Х → Y, которое ложно тогда и только тогда, когда Х – истинно, а Y – ложно. В разговорной речи импликация высказываний соответствует составлению высказывания вида: «Х имплицирует Y», «из Х следует Y», «если Х, то Y», «Х достаточно для Y», «Х только тогда, когда Y», «Y необходимо для Х», «Y тогда, когда Х». В обозначении Х → Y Х – посылка, Y – заключение.

Употребление в повседневной речи слов «если…, то…» несколько отличается от использования их в дискретной математике. Так в повседневной речи, если высказывание X ложно, то сложное высказывание Х → Y вообще не имеет смысла. В теории при ложном высказывании X значение сложного высказывания (импликации) всегда истинно.

Пример. Пусть даны высказывания A=«по проводнику протекает электричес­кий ток» и B = «вокруг проводника есть магнитное поле». Тогда формула A®B отражает высказывание «если по проводнику протекает электрический ток, то вокруг проводника возникает магнитное поле».

Эквиваленцией двух высказываний Х и Y называется высказывание Х ↔ Y, которое истинно тогда и только тогда, когда истинностные значения высказываний Х и Y совпадают. В разговорной речи эквиваленция двух высказываний соответствует составлению нового высказывания вида «Х эквивалентно Y», «Х тогда и только тогда, когда Y», «Х необходимо и достаточно для Y».

Пример. Пусть даны высказывания A =«быть четным числом» и B =«число делится на два». Тогда формула F =(A «B) отображает высказывание «для того, чтобы число было четным необходимо и достаточно, чтобы оно делилось на два».

Правила построения сложных высказываний в виде последователь­ности пропозициональных переменных, логических связок и вспомогательных символов определяют возможность формального описания любого текста. При формальной записи сложного высказывания всегда нужно исходить из его содержания. До тех пор пока не определена логическая структура сложного высказывания, его нельзя формально описывать.

Правила выполнения логических операций над сложными высказываниями на основе заданных логических связок и пропозициональных переменных формирует алгебру высказываний.

Всякое сложное высказывание, составленное из некоторых исходных высказываний посредством применения логических операций , Ù, Ú, →, ↔, будем называть формулой алгебры высказываний. Исходные высказывания при этом могут быть постоянными, то есть иметь определенное значение И или Л, или могут не иметь определенного значения. В первом случае исходные высказывания будем называть постоянными элементарными высказываниями, во втором – переменными элементарными высказываниями. Переменные элементарные высказывания будем обозначать заглавными буквами латинского алфавита.

При вычислении по формуле учитывается приоритет операций

=> Ù => Ú => → => ↔,

где знак => обозначает убывание приоритета. При необходимости изменить естественную последовательность действий используют скобки.

Символы, соответствующие переменным элементарным высказываниям, называются пропозициональными переменными.

Пропозициональной формулой (ПФ)называется выражение, построенное из пропозициональных переменных с помощью логических операций 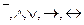(и, возможно, некоторых других) по следующим правилам:

1) каждая пропозициональная переменная есть ПФ;

2) если Х и Y – ПФ, то , , , ,

– тоже ПФ.

Если даны формулы F₁, F₂,… F_n, то истинное значение формулы F = F₁ Ù F₂ Ù…Ù F_n определяется истинностью всех формул F₁, F₂,… F_n.

Пример. Пусть даны высказывания A =«компьютер содержит микропроцессор», B =«компьютер содержит оперативную память», C =«компьютер содержит контроллеры»; D =«компьютер содержит порты ввода–вывода». Тогда формула F = A Ù B Ù C Ù D отражает высказывание «компью­тер содержит микропроцессор, оперативную память, контроллеры и порты ввода-вывода»

Если даны формулы F₁, F₂,… F_n, то истинностное значение формулы F = F₁ Ú F₂ Ú…Ú F_n определяется истинностью хотя бы одной формулы F₁, F₂,… или F_n.

Пример. Пусть даны высказывания S =«полная система булевых функций», A =«система функций содержит хотя бы одну нелинейную функцию», B =«система функций содержит хотя бы одну немонотонную функцию», C =«система функций содержит хотя бы одну не самодвойственную функцию», D =«система функций содержит хотя бы одну функцию, не сохраняющую 0», E =«система функций содержит хотя бы одну функцию, не сохраняющую 1». Тогда формула F = S «(A Ù B Ù C Ù D Ù E) отражает сложное высказывание «для того чтобы система булевых функций была полной, необходимо и достаточно, чтобы она содержала хотя бы по одной нелинейную, немо­нотонную и не самодвойственную функции, а также функции, не сохраняющие 0 и 1».