 |
Маршруты, циклы в неориентированном графе
|
|
|
|
Пусть G - неориентированный граф. Маршрутом или цепью в G называется такая последовательность (конечная или бесконечная) ребер a 1, a 2,... an..., что каждые соседние два ребра ai и ai+ 1имеют общую инцидентную вершину. Одно и то же ребро может встречаться в маршруте несколько раз. В конечном маршруте (a 1, a 2,... an) имеется первое ребро a 1и последнее ребро an. Вершина x 1, инцидентная ребру a 1, но не инцидентная ребру a 2, называется началом маршрута, а вершина xn, инцидентная ребру an, но не инцидентная ребру an- 1, называется концом маршрута.
Длиной (или мощностью) маршрута называется число ребер, входящих в маршрут, причем каждое ребро считается столько раз, сколько оно входит в данный маршрут.
Пример 3.10.
В изображенном на рис. 3.5 графе рассмотрим два маршрута из вершины x 1в вершину x 4: M 1= (a 1, a 2, a 4) и M 2= (a 1, a 2, a 5, a 6). Длина маршрута M 1 равна 3, а длина маршрута M 2 равна 4.

Рис.3.5
Замкнутый маршрут называется циклом.
Маршрут (цикл), в которой все ребра различны, называется простой цепью (циклом). Маршрут (цикл), в которой все вершины, (кроме первой и последней), различны, называется элементарной цепью (циклом).
Пример 3.11.
В приведенном на рис 3.6 графе выделим следующие маршруты:
(a 1, a 3, a 4) – простая элементарная цепь длины 3, т.к. все ребра и вершины попарно различны;
(a 2, a 4, a 3) – простой элементарный цикл, т.к. это замкнутый маршрут, у которого все ребра и вершины, кроме первой и последней, различны;
(a 1, a 2, a 4, a 3)– цепь, которая является простой, но не элементарной, т.к. все ребра различны, но вершина x 2 встречается дважды;
(a 1, a 2, a 2) –маршрут длины 3, не являющийся ни простой, ни элементарной цепью, т.к. ребро a 2и вершина x 2 встречаются дважды.

Рис.3.6
|
|
|
Пути, контуры в ориентированном графе
Понятия пути, контура в ориентированном графе аналогичны понятиям маршрута, цикла в неориентированном графе.
Путем ориентированного графа называется последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей дуги.
Число дуг пути называется длиной пути.
Путь называется контуром, если его начальная вершина совпадает с конечной вершиной.
Путь (контур), в котором все дуги различны, называется простым.
Путь (контур), в котором все вершины, кроме первой и последней, различны, называется элементарным.
Следует усвоить, что понятиям ребра, маршрута, цепи, цикла в неориентированном графе соответствуют понятия дуги, пути, ориентированной цепи, контура в ориентированном графе. Для лучшего запоминания приведем эти термины в таблице.
| Неориентированный граф | Ориентированный граф |
| ребро маршрут цикл | дуга путь контур |
Пример 3.12.
В приведенном на рис 3.7 графе выделим следующие пути:
(x 1, x 2, x 3, x 4) – простой элементарный путь, т.к. каждая вершина и каждая дуга используются не более одного раза;
(x 2, x 5, x 6, x 7, x 2) – простой элементарный контур, т.к. это замкнутый путь, в котором все дуги и вершины, кроме первой и последней, различны.

Рис. 3.7
Связность графа
Неориентированный граф называется связным, если каждая пара различных вершин может быть соединена по крайней мере одной цепью.
Ориентированный граф называется сильно связным, если для любых двух его вершин xi и xj существует хотя бы один путь, соединяющий xi с xj.
Ориентированный граф называется односторонне связным, если для любых двух его вершин по крайней мере одна достижима из другой.
Компонентой связности неориентированного графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа данного графа (максимально связный подграф).
|
|
|
Компонентой сильной связности ориентированного графа называется его сильно связный подграф, не являющийся собственным подграфом никакого другого сильно связного подграфа данного графа (максимально сильно связный подграф).
Компонентой одностронней связности неориентированного графа называется его односторонне связный подграф, не являющийся собственным подграфом никакого другого односторонне связного подграфа данного графа (максимально односторонне связный подграф).
Пусть G = (X, A) неориентированный граф с множеством вершин X = { x 1,..., xn }. Квадратная матрица S = (sij)порядка n, у которой
sij = 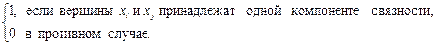

называется матрицей связности графа G.
Для ориентированного графа квадратная матрица T = (tij) порядка n, у которой
tij = 
называется матрицей односторонней связности (достижимости ).
Квадратная матрица S = (sij) порядка n, у которой
sij = 
называется матрицей сильной связности.
Пример 3.13.
У неориентированного графа, изображенного на рис. 3.8 две компоненты связности. Первая компонента связности включает вершины x 1, x 2, x 4, x 5,а вторая состоит из одной вершины x 3.

Рис.3.8
Матрица связности этого графа имеет вид:
S = 
Мы видим, что 1-ая, 2-ая, 4-ая и 5-ая строки матрицы S одинаковы.
Пример 3.14.
У ориентированного графа, изображенного на рис. 3.9 две компоненты сильной связности. Первая компонента связности включает вершины x 1, x 2, x 3, x 5,а вторая состоит из одной вершины x 4. Действительно, для любой пары вершин из множества { x 1, x 2, x 3, x 5}существует хотя бы один путь, соединяющий эти вершины. Например, путь (x 1, x 2, x 5, x 3, x 1) соединяет все эти вершины. Из вершины x 4 нет пути ни в одну вершину графа. 
Рис. 3.9
Матрица сильной связности этого графа имеет вид:
S = 
Мы видим, что 1-ая, 2-ая, 3-ая и 5-ая строки матрицы S одинаковы.
|
|
|


