Множества мощности континуума

Существуют бесконечные множества, элементы которых нельзя перенумеровать. Такие множества называются несчетными.

Теорема Кантора. Множество всех точек отрезка [0, 1] несчетно.

Доказательство.

Пусть множество точек отрезка [0, 1] счетно. Значит, эти точки можно перенумеровать, т. е. расположить в виде последовательности x ₁, x ₂ … x_n, ….

 

Рис. 1.7

 

Разобьем отрезок [0, 1] на три равные части. Где бы ни находилась точка x ₁, она не может принадлежать всем отрезкам , , 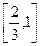. Поэтому среди них есть отрезок D₁, не содержащий точку x ₁ (рис. 1.7). Возьмем этот отрезок D₁ и разделим его на три равные части. Среди них всегда есть отрезок D₂, не содержащий точку x ₂. Разделим этот отрезок на три равные части и т. д. Получим последовательность отрезков D₁ É D₂ É D₃ É…ÉD _n É…. В силу аксиомы Кантора сходится к некоторой точке x при n ® ¥. По построению эта точка x принадлежит каждому отрезку D₁, D₂, D₃,…, D _n, …, т. е. она не может совпадать ни с одной из точек x ₁, x ₂, … x_n, …, т. е. последовательность x ₁, x ₂ … x_n, …не исчерпывает всех точек отрезка [0, 1], что противоречит первоначальному предположению. Теорема доказана.

Множество, эквивалентное множеству всех точек отрезка [0, 1] называется множеством мощности континуума.

Так как множества точек интервалов, отрезков и всей прямой эквивалентны между собой, то все они имеют мощность континуума.

Чтобы доказать, что данное множество имеет мощность континуума, достаточно указать взаимно однозначное соответствие между данным множеством и множеством точек отрезка, интервала или всей прямой.

Пример 1.24.

Из рис. 1.8 следует, что множество точек параболы y = x ² эквивалентно множеству точек прямой –¥ < x < ¥ и, следовательно, имеет мощность континуума.

Рис.1.8

Установить мощность континуума можно также, используя следующие теоремы о множествах мощности континуума (приводятся без доказательств).

Теорема 1. Множество всех подмножеств счетного множества счетно.

Теорема 2. Множество иррациональных чисел имеет мощность континуума.

Теорема 3. Множество всех точек n- мерного пространства при любом n имеет мощность континуума.

Теорема 4. Множество всех комплексных чисел имеет мощность континуума.

Теорема 5. Множество всех непрерывных функций, определенных на отрезке [ a, b ] имеет мощность континуума.

Итак, мощности бесконечных множеств могут различаться. Мощность континуума больше, чем мощность счетного множества. Ответ на вопрос, существуют ли множества более высокой мощности, чем мощность континуума, дает следующая теорема (приводится без доказательства).

Теорема о множествах высшей мощности. Множество всех подмножеств данного множества имеет более высокую мощность, чем данное множество.

Из этой теоремы следует, что множеств с максимально большой мощностью не существует.

Контрольные вопросы к теме 1

1. Пусть a Î А. Следует ли отсюда, что { a } А?

2. В каком случае А А Ç В?

3. Назовите множество, которое является подмножеством любого множества.

4. Может ли быть множество эквивалентно своему подмножеству?

5. Мощность какого множества больше: множества натуральных чисел или множества точек отрезка [0, 1]?

ТЕМА 2. ОТНОШЕНИЯ. ФУНКЦИИ

 

Отношения. Основные понятия и определения

Определение 2.1. Упорядоченной парой < x, y > называется совокупность двух элементов x и y, расположенных в определенном порядке.

Две упорядоченные пары < x, y > и < u, v> равны межу собой тогда и только тогда, когда x = u и y = v.

Пример 2.1.

< a, b >, <1, 2>, < x, 4> – упорядоченные пары.

Аналогично можно рассматривать тройки, четверки, n -ки элементов < x ₁, x ₂, … x_n >.

Определение 2.2. Прямым (или декартовым) произведением двух множеств A и B называется множество упорядоченных пар, таких, что первый элемент каждой пары принадлежит множеству A, а второй – множеству B:

A ´ B = {< a, b >, ç a Î А и b Ï В }.

В общем случае прямым произведением n множеств А ₁, А ₂,… А_n называется множество А ₁ ´ А ₂ ´ …´ А_n, состоящее из упорядоченных наборов элементов < a ₁, a ₂, …, a_n > длины n, таких, что i- ый a_i принадлежит множеству А_i, a_i Î А_i.

Пример 2.2.

Пусть А = {1, 2}, В = {2, 3}.

Тогда A ´ B = {<1, 2>, <1, 3>,<2, 2>,<2, 3>}.

Пример 2.3.

Пусть А = { x ç0 £ x £ 1} и B = { y ç2 £ y £ 3}

Тогда A ´ B = {< x, y >, ç0 £ x £ 1и2 £ y £ 3}.

Таким образом, множество A ´ B состоит из точек, лежащих внутри и на границе прямоугольника, образованного прямыми x = 0 (ось ординат), x = 1, y = 2и y = 3.

Французский математик и философ Декарт впервые предложил координатное представление точек плоскости. Это исторически первый пример прямого произведения.

Определение 2.3. Бинарным (или двуместным) отношением r называется множество упорядоченных пар.

Если пара < x, y > принадлежит r, то это записывается следующим образом: < x, y > Î r или, что то же самое, xr y.

Пример2.4.

r = {<1, 1>, <1, 2>, <2, 3>}

Аналогично можно определить n -местное отношение как множество упорядоченных n -ок.

Так как бинарное отношение – множество, то способы задания бинарного отношения такие же, как и способы задания множества (см. разд. 1.1). Бинарное отношение может быть задано перечислением упорядоченных пар или указанием общего свойства упорядоченных пар.

Пример 2.5.

1. r = {<1, 2>, <2, 1>, <2, 3>} – отношение задано перечислением упорядоченных пар;

2. r = {< x, y > ç x + y = 7, x, y – действительные числа} – отношение задано указанием свойства x + y = 7.

Кроме того, бинарное отношение может быть задано матрицей бинарного отношения. Пусть А = { a ₁, a ₂, …, a_n } – конечное множество. Матрица бинарного отношения C есть квадратная матрица порядка n, элементы которой c_ij определяются следующим образом:

c_ij =

Пример 2.6.

А = {1, 2, 3, 4}. Зададим бинарное отношение r тремя перечисленными способами.

1. r = {<1, 2>, <1, 3>, <1, 4>, <2, 3>, <2, 4>, <3, 4>} – отношение задано перечислением всех упорядоченных пар.

2. r = {< a_i, a_j > ç a_i < a_j; a_i, a_j Î А } – отношение задано указанием свойства "меньше" на множестве А.

3. – отношение задано матрицей бинарного отношения C.

Пример 2.7.

Рассмотрим некоторые бинарные отношения.

1. Отношения на множестве натуральных чисел.

а) отношение £ выполняется для пар <1, 2>, <5, 5>, но не выполняется для пары <4, 3>;

б) отношение "иметь общий делитель, отличный от единицы" выполняется для пар <3, 6>, <7, 42>, <21, 15>, но не выполняется для пары <3, 28>.

2. Отношения на множестве точек действительной плоскости.

а) отношение "находиться на одинаковом расстоянии от точки (0, 0)" выполняется для точек (3, 4) и (–2, Ö21), но не выполняется для точек (1, 2) и (5, 3);

б) отношение "быть симметричным относительно оси OY " выполняется для всех точек (x, y) и (– x, – y).

3. Отношения на множестве людей.

а) отношение "жить в одном городе";

б) отношение "учиться в одной группе";

в) отношение "быть старше".

Определение 2.4. Областью определения бинарного отношения r называется множество D_r = {x çсуществует y, что xr y}.

Определение 2.5. Областью значений бинарного отношения r называется множество R_r = {y çсуществует x, что xr y}.

Определение 2.6. Областью задания бинарного отношения r называется множество M_r = D_r ÈR_r.

Используя понятие прямого произведения, можно записать:

r Î D_r ´ R_r

Если D_r = R_r = A, то говорят, что бинарное отношение r задано на множестве A.

Пример 2.8.

Пусть r = {<1, 3>, <3, 3>, <4, 2>}.

Тогда D_r = {1, 3, 4}, R_r = {3, 2}, M_r = {1, 2, 3, 4}.

 

Операции над отношениями

Так как отношения являются множествами, то все операции над множествами справедливы для отношений.

Пример 2.9.

r ₁ = {<1, 2>, <2, 3>, <3, 4>}.

r ₂ = {<1, 2>, <1, 3>, <2, 4>}.

r ₁ È r ₂ = {<1, 2>, <1, 3>, <2, 3>, <2, 4>, <3, 4>}.

r ₁ Ç r ₂ = {<1, 2>}.

r ₁ \ r ₂ = {<2, 3>, <3, 4>}.

Пример 2.10.

Пусть R – множество действительных чисел. Рассмотрим на этом множестве следующие отношения:

r ₁ – " £ "; r ₂ – " = "; r ₃ – " < "; r ₄ – " ³ "; r ₅ – " > ".

Тогда

r ₁ = r ₂ È r ₃;

r ₂ = r ₁ Ç r ₄;

r ₃ = r ₁ \ r ₂;

r ₁ = ;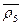

Определим еще две операции над отношениями.

Определение 2.7. Отношение называется обратным к отношению r (обозначается r ^{– 1}), если

r ^{– 1} = {< x, y > ç< y, x > Î r }.

Пример 2.11.

r = {<1, 2>, <2, 3>, <3, 4>}.

r ^{– 1}= {<2, 1>, <3, 2>, <4, 3>}.

Пример 2.12.

r = {< x, y > ç x – y = 2, x, y Î R }.

r ^{– 1} = {< x, y > ç< y, x > Î r } = r ^{– 1} = {< x, y > ç y – x = 2, x, y Î R } = {< x, y > ç– x + y = 2, x, y Î R }.

Определение 2.8. Композицией двух отношений r и s называется отношение

s r = {< x, z > çсуществует такое y, что < x, y > Î r и < y, z > Î s }.

Пример 2.13.

r = {< x, y > ç y = sinx }.

s = {< x, y > ç y = Ö x }.

s r = {< x, z > çсуществует такое y, что < x, y > Î r и < y, z > Î s } = {< x, z > çсуществует такое y, что y = sinx и z = Ö y } = {< x, z > ç z = Ö sinx }.

Определение композиции двух отношенийсоответствует определению сложной функции:

y = f (x), z = g (y) Þ z = g (f (x)).

Пример 2.14.

r = {<1, 1>, <1, 2>, <1, 3>, <3, 1>}.

s = {<1, 2>, <1, 3>, <2, 2>, <3, 2>, <3, 3>}.

Процесс нахождения s r в соответствии с определением композиции удобно изобразить таблицей, в которой реализуется перебор всех возможных значений x, y, z. для каждой пары < x, y > Î r нужно рассмотреть все возможные пары < y, z > Î s (табл. 2.1).

Таблица 2.1

< x, y > Î r	< y, z > Î s	< x, z > Î s r
<1, 1> <1, 1> <1, 2> <1, 3> <1, 3> <3, 1> <3, 1>	<1, 2> <1, 3> <2, 2> <3, 2> <3, 3> <1, 2> <1, 3>	<1, 2> <1, 3> <1, 2> <1, 2> <1, 3> <3, 2> <3, 3>

Заметим, что первая, третья и четвертая, а также вторая и пятая строки последнего столбца таблицы содержат одинаковые пары. Поэтому получим:

s r = {<1, 2>, <1, 3>, <3, 2>, <3, 3>}.

 

Свойства отношений

Определение 2.9. Отношение r называется рефлексивным на множестве X, если для любого x Î X выполняется xr x.

Из определения следует, что всякий элемент < x, x > Î r.

Пример 2.15.

а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <2, 2>, <3, 1>, <3, 3>}. Отношение r рефлексивно. Если X – конечное множество, то главная диагональ матрицы рефлексивного отношения содержит только единицы. Для нашего примера

.

б) Пусть X – множество действительных чисел и r отношение равенства. Это отношение рефлексивно, т.к. каждое число равно самому себе.

в) Пусть X – множество людей и r отношение "жить в одном городе". Это отношение рефлексивно, т.к. каждый живет в одном городе сам с собой.

Определение 2.10. Отношение r называется симметричным на множестве X, если для любых x, y Î X из xry следует yr x.

Очевидно, что r симметрично тогда и только тогда, когда r = r^{– 1}.

Пример 2.16.

а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <1, 3>, <2, 1>, <3, 1>, <3, 3>}. Отношение r симметрично. Если X – конечное множество, то матрица симметричного отношения симметрична относительно главной диагонали. Для нашего примера

.

б) Пусть X – множество действительных чисел и r отношение равенства. Это отношение симметрично, т.к. если x равно y, то и y равно x.

в) Пусть X – множество студентов и r отношение "учиться в одной группе". Это отношение симметрично, т.к. если x учится в одной группе с y, то и y учится в одной группе с x.

Определение 2.11. Отношение r называется транзитивным на множестве X, если для любых x, y, z Î X из xry и yr z следует xr z.

Одновременное выполнение условий xry, yr z, xr z означает, что пара < x, z > принадлежит композиции r r. Поэтому для транзитивности r необходимо и достаточно, чтобы множество r r являлось подмножеством r, т. е. r r Í r.

Пример 2.17.

а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <2, 3>, <1, 3>}. Отношение r транзитивно, т. к. наряду с парами < x, y >и < y, z >имеется пара< x, z >. Например, наряду с парами <1, 2>, и <2, 3> имеется пара <1, 3>.

б) Пусть X – множество действительных чисел и r отношение £ (меньше или равно). Это отношение транзитивно, т.к. если x £ y и y £ z, то x £ z.

в) Пусть X – множество людей и r отношение "быть старше". Это отношение транзитивно, т.к. если x старше y и y старше z, то x старше z.

Определение 2.12. Отношение r называется отношением эквивалентности на множестве X, если оно рефлексивно, симметрично и транзитивно на множестве X.

Пример 2.18.

а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <2, 2>, <3, 3>}. Отношение r является отношением эквивалентности.

б) Пусть X – множество действительных чисел и r отношение равенства. Это отношение эквивалентности.

в) Пусть X – множество студентов и r отношение "учиться в одной группе". Это отношение эквивалентности.

Пусть r – отношение эквивалентности на множестве X.

Определение 2.13. Пусть r – отношение эквивалентности на множестве X и x Î X. Классом эквивалентности, порожденным элементом x, называется подмножество множества X, состоящее из тех элементов y Î X, для которых xry. Класс эквивалентности, порожденный элементом x, обозначается через [ x ].

Таким образом, [ x ] = { y Î X | xry }.

Классы эквивалентности образуют разбиение множества X, т. е. систему непустых попарно непересекающихся его подмножеств, объединение которых совпадает со всем множеством X.

Пример 2.19.

а) Отношение равенства на множестве целых чисел порождает следующие классы эквивалентности: для любого элемента x из этого множества [ x ] = { x }, т.е. каждый класс эквивалентности состоит из одного элемента.

б) Класс эквивалентности, порожденный парой < x, y > определяется соотношением:

[< x, y >] = .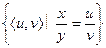

Каждый класс эквивалентности, порожденный парой < x, y >, определяет одно рациональное число.

в) Для отношения принадлежности к одной студенческой группе классом эквивалентности является множество студентов одной группы.

Определение 2.14. Отношение r называется антисимметричным на множестве X, если для любых x, y Î X из xry и yr x следует x = y.

Из определения антисимметричности следует, что всякий раз, когда пара < x, y > принадлежит одновременно r и r^{– 1}, должно выполняться равенство x = y. Другими словами, r Ç r^{– 1} состоит только из пар вида < x, x >.

Пример 2.20.

а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <1, 3>, <2, 2>, <2, 3>, <3, 3>}. Отношение r антисимметрично.

Отношение s = {<1, 1>, <1, 2>, <1, 3>, <2, 1>, <2, 3>, <3, 3>} неантисимметрично. Например, <1, 2> Î s, и <2, 1> Î s, но 1 ¹2.

б) Пусть X – множество действительных чисел и r отношение £ (меньше или равно). Это отношение антисимметрично, т.к. если x £ y, и y £ x, то x = y.

Определение 2.15. Отношение r называется отношением частичного порядка (или просто частичным порядком) на множестве X, если оно рефлексивно, антисимметрично и транзитивно на множестве X. Множество X в этом случае называют частично упорядоченным и указанное отношение часто обозначают символом £, если это не приводит к недоразумениям.

Отношение, обратное отношению частичного порядка будет, очевидно, отношением частичного порядка.

Пример 2.21.

а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <1, 3>, <2, 2>, <2, 3>, <3, 3>}. Отношение r есть отношение частичного порядка.

б) Отношение А Í В на множестве подмножеств некоторого множества U есть отношение частичного порядка.

в) Отношение делимости на множестве натуральных чиселесть отношение частичного порядка.

 

Функции. Основные понятия и определения

В математическом анализе принято следующее определение функции.

Переменная y называется функцией от переменной x, если по некоторому правилу или закону каждому значению x соответствует одно определенное значение y = f (x). Область изменения переменной x называется областью определения функции, а область изменения переменной y – областью значений функции. Если одному значению x соответствует несколько (и даже бесконечно много значений y), то функция называется многозначной. Впрочем, в курсе анализа функций действительных переменных избегают многозначных функций и рассматривают однозначные функции.

Рассмотрим другое определение функции с точки зрения отношений.

Определение 2.16. Функцией называется любое бинарное отношение, которое не содержит двух пар с равными первыми компонентами и различными вторыми.

Такое свойство отношения называется однозначностью или функциональностью.

Пример 2.22.

а) {<1, 2>, <3, 4>, <4, 4>, <5, 6>} – функция.

б) {< x, y >: x, y Î R, y = x ²} – функция.

в) {<1, 2>, <1, 4>, <4, 4>, <5, 6>} – отношение, но не функция.

Определение 2.17. Если f – функция, то D_f – область определения, а R_f – область значений функции f.

Пример 2.23.

Для примера 2.22 а) D_f – {1, 3, 4, 5}; R_f – {2, 4, 6}.

Для примера 2.22 б) D_f = R_f = (–¥, ¥).

Каждому элементу x D_f функция ставит в соответствие единственный элемент y R_f. Это обозначается хорошо известной записью y = f (x). Элемент x называется аргументом функции или прообразом элемента y при функции f, а элемент y значением функции f на x или образом элемента x при f.

Итак, из всех отношений функции выделяются тем, что каждый элемент из области определения имеет единственный образ.

Определение 2.18. Если D_f = X и R_f = Y, то говорят, что функция f определена на X и принимает свои значения на Y, а f называют отображением множества X на Y (X ® Y).

Определение 2.19. Функции f и g равны, если их область определения – одно и то же множество D, и для любого x Î D справедливо равенство f (x) = g (x).

Это определение не противоречит определению равенства функций как равенства множеств (ведь мы определили функцию как отношение, т. е. множество): множества f и g равны, тогда и только тогда, когда они состоят из одних и тех же элементов.

Определение 2.20. Функция (отображение) f называется сюръективной или просто сюръекцией, если ля любого элемента y Y существует элемент x Î X, такой, что y = f (x).

Таким образом, каждая функция f является сюръективным отображением (сюръекцией) D_f ® R_f.

Если f – сюръекция, а X и Y – конечные множества, то ³ .

Определение 2.21. Функция (отображение) f называется инъективной или просто инъекцией или взаимно однозначной, если из f (a) = f (b) следует a = b.

Определение 2.22. Функция (отображение) f называется биективной или просто биекцией, если она одновременно инъективна и сюръективна.

Если f – биекция, а X и Y – конечные множества, то = .

Определение 2.23. Если область значений функции D_f состоит из одного элемента, то f называется функцией-константой.

Пример 2.24.

а) f (x) = x ² есть отображение множества действительных чисел на множество неотрицательных действительных чисел. Т.к. f (– a) = f (a), и a ¹ – a, то эта функция не является инъекцией.

б) Для каждого x R = (– , ) функция f (x) = 5 – функция-константа. Она отображает множество R на множество {5}. Эта функция сюръективна, но не инъективна.

в) f (x) = 2 x + 1 является инъекцией и биекцией, т.к. из 2 x ₁ +1 = 2 x ₂ +1 следует x ₁ = x ₂.

Определение 2.24. Функция, реализующая отображение X ₁ ´ X ₂ ´...´ X_n ® Y называется n-местной функцией.

Пример 2.25.

а) Сложение, вычитание, умножение и деление являются двуместными функциями на множестве R действительных чисел, т. е. функциями типа R ² ® R.

б) f (x, y) = 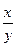– двуместная функция, реализующая отображение R ´ (R \ )® R. Эта функция не является инъекцией, т.к. f (1, 2) = f (2, 4).

в) Таблица выигрышей лотереи задает двуместную функцию, устанавливающую соответствие между парами из N ² (N – множество натуральных чисел) и множеством выигрышей.

Поскольку функции являются бинарными отношениями, то можно находить обратные функции и применять операцию композиции. Композиция любых двух функций есть функция, но не для каждой функции f отношение f ^–1 является функцией.

Пример 2.26.

а) f = {<1, 2>, <2, 3>, <3, 4>, <4, 2>} – функция.

Отношение f ^–1 = {<2, 1>, <3, 2>, <4, 3>, <2, 4>} не является функцией.

б) g = {<1, a >, <2, b >, <3, c >, <4, D >} – функция.

g ^-1 = {< a, 1>, < b, 2>, < c, 3>, < D, 4>} тоже функция.

в) Найдем композицию функций f из примера а) и g ^-1 из примера б). Имеем g ^{-1 f} = {< a, 2>, < b, 3>, < c, 4>, < d, 2>}.

fg ^-1 = Æ.

Заметим, что (g ^{-1 f} )(a) = f (g ^-1(a)) = f (1) = 2; (g ^{-1 f} )(c) = f (g ^-1(c)) = f (3) = 4.

Элементарной функцией в математическом анализе называется всякая функция f, являющаяся композицией конечного числа арифметических функций, а также следующих функций:

1) Дробно-рациональные функции, т.е. функции вида

a ₀ + a ₁ x +... + a_nxⁿ

b ₀ + b ₁ x +... + b_mx^m.

2) Степенная функция f (x) = x^m, где m – любое постоянное действительное число.

3) Показательная функция f (x) = e^x.

4) логарифмическая функция f (x) = log_ax, a >0, a 1.

5) Тригонометрические функции sin, cos, tg, ctg, sec, csc.

6) Гиперболические функции sh, ch, th, cth.

7) Обратные тригонометрические функции arcsin, arccos и т.д.

Например, функция log ²(x ³ + sincos 3 x) является элементарной, т.к. она есть композиция функций cosx, sinx, x ³, x ₁ + x ₂, logx, x ².

Выражение, описывающее композицию функций, называется формулой.

Для многоместной функции справедлив следующий важный результат, полученный А. Н. Колмогоровым и В. И. Арнольдом в 1957 г. и являющийся решением 13-ой проблемы Гильберта:

Теорема. Всякая непрерывная функция n переменных представима в виде композиции непрерывных функций двух переменных.

 

Способы задания функций

 

1. Наиболее простой способ задания функций – это таблицы (табл. 2.2):

Таблица 2.2

x	x 1	x 2	...	xn
f (x)	f (x 1)	f (x 2)	...	f (xn)

 

Пример 2.27.

Бросается игральная кость. Пусть k – число выпавших очков, а p (k) – вероятность того, что при случайном бросании кости выпадет k очков, k = 1, 2,..., 6.

В этом случае функция p (k) может быть задана следующей таблицей (табл. 2.3):

Таблица 2.3

k
p (k)	1/6	1/6	1/6	1/6	1/6	1/6

 

Однако, таким образом могут быть заданы функции, определенные на конечных множествах.

Если функция, определенная на бесконечном множестве (отрезке, интервале), задана в конечном числе точек, например, в виде тригонометрических таблиц, таблиц специальных функций и т.п., то для вычисления значений функций в промежуточных точках пользуются правилами интерполяции.

2. Функция может быть задана в виде формулы, описывающей функцию как композицию других функций. Формула задает последовательность вычисления функции.

Пример 2.28.

f (x) = sin (x + Ö x) является композицией следующих функций:

g (y) = Ö y; h (u, v) = u + v; w (z) = sinz.

3. Функция может быть задана в виде рекурсивной процедуры. Рекурсивная процедура задает функцию, определенную на множестве натуральных чисел, т. е. f (n), n = 1, 2,... следующим образом: а) задается значение f (1) (или f (0)); б) значение f (n + 1) определяется через композицию f (n) и других известных функций. Простейшим примером рекурсивной процедуры является вычисление n!: а) 0! = 1; б) (n + 1)! = n!(n + 1). Многие процедуры численных методов являются рекурсивными процедурами.

4. Возможны способы задания функции, не содержащие способа вычисления функции, а только описывающие ее. Например:

f_M (x) =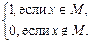

Функция f_M (x) – характеристическая функция множества M.

Итак, по смыслу нашего определения, задать функцию f – значит задать отображение X ® Y, т.е. определить множество X ´ Y, поэтому вопрос сводится к заданию некоторого множества. Однако можно определить понятие функции, не используя языка теории множеств, а именно: функция считается заданной, если задана вычислительная процедура, которая по заданному значению аргумента находит соответствующее значение функции. Функция, определенная таким образом, называется вычислимой.

Пример 2.29.

Процедура определения чисел Фибоначчи, задается соотношением

F_n = F_{n- 1} + F_{n- 2} (n ³ 2) (2.1)

с начальными значениями F ₀ = 1, F ₁ = 1.

Формула (2.1) вместе с начальными значениями определяет следующий ряд чисел Фибоначчи:

n	0 1 2 3 4 5 6 7 8 9 10 11 …
Fn	1 1 2 3 5 8 13 21 34 55 89 144 …

 

Вычислительная процедура определения значения функции по заданному значению аргумента есть не что иное, как алгоритм.

 

Контрольные вопросы к теме 2

 

1. Укажите способы задания бинарного отношения.

2. Главная диагональ матрицы какого отношения содержит только единицы?

3. Для какого отношения r всегда выполняется условие r = r^{– 1}?

4. Для какого отношения r всегда выполняется условие r r Í r.

5. Ввести отношения эквивалентности и частичного порядка на множестве всех прямых на плоскости.

6. Укажите способы задания функций.

7. Какое из следующих утверждений справедливо?

а) Всякое бинарное отношение есть функция.

б) Всякая функция есть бинарное отношение.

Тема 3. ГРАФЫ

 

Первая работа по теории графов принадлежащая Эйлеру, появилась в 1736 году. Вначале эта теория была связана с математическими головоломками и играми. Однако впоследствии теория графов стала использоваться в топологии, алгебре, теории чисел. В наше время теория графов находит применение в самых разнообразных областях науки, техники и практической деятельности. Она используется при проектировании электрических сетей, планировании транспортных перевозок, построении молекулярных схем. Применяется теория графов также в экономике, психологии, социологии, биологии.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: