 |
Теория вероятностей и математическая статистика – основной инструментарий для прикладной статистики
|
|
|
|
Математическая статистика
Случайная величина – переменная величина, принимающая одно из возможных значений в зависимости от случайных обстоятельств. Случайная величина считается полностью заданной своим распределением, если указан закон, по которому можно вычислить вероятность попадания случайной величины в любое подмножество ее возможных значений.
Распределение вероятностей – совокупность всех возможных значений случайной величины и соответствующих им вероятностей.
Случайная величина называется дискретной, если она принимает конечное или счетной число значений. Дискретная величина задается с помощью ряда распределения – функции, ставящей в соответствие каждому возможному значению случайной величины определенную вероятность. Таким образом, ряд распределения - это конечное или счетное множество пар элементов:

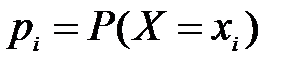
Так как случайная величина Х примет обязательно какое-нибудь из своих значений  , сумма вероятностей
, сумма вероятностей  всех возможных значений равно единице, т.е.
всех возможных значений равно единице, т.е.  для случайной величины, принимающей конечное число n возможных значений, и
для случайной величины, принимающей конечное число n возможных значений, и  для дискретной случайной величины, принимающей счетное число значений.
для дискретной случайной величины, принимающей счетное число значений.
Обычно ряд распределения удобно изображать в виде таблицы, где в верхней строке указаны возможные значения  дискретной случайной величины Х, в нижней – соответствующие вероятности того, что Х примет значение
дискретной случайной величины Х, в нижней – соответствующие вероятности того, что Х примет значение  .
.
Х= 


 .
.
Полигоном (многоугольником) распределения называется графическое изображение ряда распределения. Для того чтобы построить полигон распределения необходимо отложить возможные значения случайной величины  по оси абсцисс, а соответствующие им вероятности по оси ординат.
по оси абсцисс, а соответствующие им вероятности по оси ординат.
Множество значений непрерывной случайной величины несчетно и обычно представляет собой некоторый промежуток, конечный или бесконечный. Непрерывная величина принимает возможные значения, заполняющие сплошь заданный интервал, причем для любого х из этого интервала существует предел:
|
|
|

Функция  называется плотностью распределения или дифференциальным законом распределения.
называется плотностью распределения или дифференциальным законом распределения.
Плотность распределения обладает следующими свойствами:
1) 
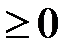 ;
;
2) Для любых 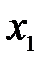 <
<  выполняется равенство:
выполняется равенство:  =
= 
3) Интеграл по всей числовой прямой от плотности распределения вероятностей равен 1, т.е.  .
.
4) Вероятность того, что непрерывная случайная величина примет конкретное значение, равна 0, т.е.  .
.
График плотности распределения носит название кривой распределения. 
Функцией распределения F(x) случайной величины Х, принимающей любое действительное значение x, называется вероятность того, что случайная величина Х приимет значение меньшее чем х, то есть  . Функцию распределения F(x) называют также интегральным законом распределения.
. Функцию распределения F(x) называют также интегральным законом распределения.
Для дискретной случайной величины функция F(x) вычисляется по формуле:
 ,
,
где суммирование осуществляется по всем значениям i, для которых  .
.
Для непрерывной случайной величины интегральный закон выражается формулой:  , где функция
, где функция  - плотность распределения.
- плотность распределения.
Функцией распределения F(x) обладает следующими свойствами:
1) 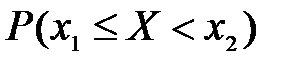 = F(x2) – F(x1);
= F(x2) – F(x1);
2)  , если
, если  ;
;
3) 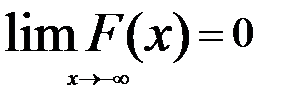 ;
;
4)  ;
;
5)  (для непрерывной случайной величины).
(для непрерывной случайной величины).
График функции распределения F(x) для непрерывных случайных величин называется интегральной кривой распределения.
Числовые характеристики случайных величин. Функция распределения дает полную информацию о законе распределения случайной величины. Однако часто бывает достаточно знать одну или несколько числовых характеристик случайной величины, дающих наглядное представление о ней, например, некоторое «среднее» число, вокруг которого группируются значения случайной величины (центр группирования распределения), и ту или иную характеристику вариации значений случайной величины (степень рассеивания ее значений).
|
|
|
Основной характеристикой центра группирования случайной величины в генеральной совокупности является ее математическое ожидание. Выборочным аналогом математического ожидания является среднее значение  .
.
Математическое ожидание М(х) дискретной случайной величины определяется по формуле:  (1.1)
(1.1)
Если случайная величина Х непрерывна и  - ее плотность распределения, то математическим ожиданием называется интеграл:
- ее плотность распределения, то математическим ожиданием называется интеграл:
 , (1.2)
, (1.2)
в тех случаях, когда существует интеграл  .
.
Приведем без доказательств основные свойства математического ожидания.
1. Математическое ожидание постоянной равно этой постоянной, т.е. если с – постоянная, то М(Х)=с.
2. Постоянную величину можно выносить за знак математического ожидания, т.е. если Х – случайная величина, а с – постоянная, то М(сХ)=с*М(Х).
3. Математическое ожидание суммы случайных величин равно сумме математических ожиданий этих случайных величин, т.е. если определены МХ и МY, то определено математическое ожидание М(Х+Y), причем М(Х+Y)= МХ+ МY. Это свойство верно как для зависимых, так и независимых случайных величин.
4. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих случайных величин, т.е. если Х и Y – независимые случайные величины, то М(ХY)= МХ* МY.
Модальное значение (или просто мода) Мо случайной величины определяется как такое возможное значение исследуемого признака, при котором значение плотности вероятности  (в непрерывном случае) или вероятности
(в непрерывном случае) или вероятности 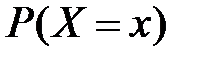 (в дискретном случае) достигает своего максимума. Мода представляет собой наиболее часто встречающееся значение случайной величины.
(в дискретном случае) достигает своего максимума. Мода представляет собой наиболее часто встречающееся значение случайной величины.
Медиана Ме исследуемого признака определяется как его средневероятное значение, т.е. такое значение, которое обладает следующим свойством: вероятность того, что случайная величина окажется больше Ме, равна вероятности того, что она окажется меньше. Для обладающих непрерывной плотностью случайных величин выполняется условие:
 (1.3)
(1.3)
и медиану можно определить как такое значение 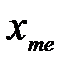 на оси абсцисс, при котором прямая, параллельная оси ординат и проходящая через точку
на оси абсцисс, при котором прямая, параллельная оси ординат и проходящая через точку 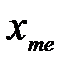 делит площадь под кривой плотности на две равные части. В некоторых случаях дискретных распределений может не существовать величины, точно удовлетворяющей сформулированному требованию. Поэтому для дискретных величин медиану можно определить как любое
делит площадь под кривой плотности на две равные части. В некоторых случаях дискретных распределений может не существовать величины, точно удовлетворяющей сформулированному требованию. Поэтому для дискретных величин медиану можно определить как любое 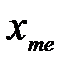 , лежащее между соседними возможными значениями
, лежащее между соседними возможными значениями  и
и  , такими, что
, такими, что  <0,5 и
<0,5 и 
 0,5.
0,5.
|
|
|
Характеристики вариации уточняют представление о распределении вероятностей случайной величины. Они дают представление о степени рассеивания случайной величины относительно центра группирования. Наиболее часто используемыми характеристиками вариации являются дисперсия случайной величины и ее среднеквадратическое отклонение.
Дисперсией случайной величины Х называется число DX, равное математическому ожиданию квадрата отклонения случайной величины от своего математического ожидания:  . (1.4)
. (1.4)
Если известен закон распределения случайной величины Х, то для дискретной и непрерывной случайных величин дисперсию можно вычислить соответственно по формулам:  (1.5)
(1.5)
 , (1.6)
, (1.6)
где  - плотность распределения случайной величины.
- плотность распределения случайной величины.
В качестве меры рассеивания случайной величины наряду с дисперсией используют среднеквадратическое отклонение  , равное квадратному корню из дисперсии случайной величины:
, равное квадратному корню из дисперсии случайной величины:  =
=  . (1.7)
. (1.7)
Среднеквадратическое отклонение случайной величины выражается в тех же единицах, что и сама случайная величина и ее математическое ожидание.
Приведем без доказательств основные свойства дисперсии. Свойства среднеквадратического отклонения непосредственно вытекают из соответствующих свойств дисперсии.
1) Дисперсия постоянной с равна нулю: D(c)=0.
2) Дисперсия произведения случайной величины Х на постоянную с равна произведению дисперсии случайной величины Х на квадрат постоянной:  .
.
3) Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий:  .
.
4) Дисперсия случайной величины Х не изменится, если к ней прибавить постоянную с, т.е.  .
.
Моменты случайной величины обобщают понятия математического ожидания и дисперсии.
|
|
|
Моментом k – порядка называется математическое ожидание k –й степени отклонения случайной величины Х от некоторой постоянной с.
Если в качестве с берется нуль, моменты называют начальными, то есть
 . (1.8)
. (1.8)
Если с=М(Х), то моменты называются центральными, то есть
 . (1.9)
. (1.9)
Таким образом, математическое ожидание – ни что иное, как первый начальный момент, а дисперсия – второй центральный момент.
Существует формула, связывающая центральные моменты с начальными:
 . (1.10)
. (1.10)
Для первых четырех моментов эта формула дает следующие равенства:
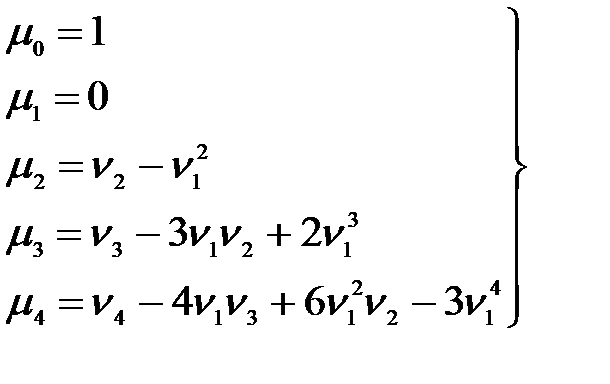 (1.11)
(1.11)
Формула  может быть использована для нахождения дисперсии случайной величины:
может быть использована для нахождения дисперсии случайной величины:  (1.12)
(1.12)
В теории и практических приложениях используют две числовые характеристики случайной величины, основанные на центральных моментах третьего и четвертого порядков соответственно – коэффициент асимметрии  и эксцесс
и эксцесс  . Данные коэффициенты дают представление о форме плотности распределения или многоугольника распределения.
. Данные коэффициенты дают представление о форме плотности распределения или многоугольника распределения.
Коэффициентом асимметрии случайной величины Х называется число, равное отношению третьего центрального момента к кубу среднеквадратического отклонения случайной величины Х:  (1.13)
(1.13)
Коэффициент асимметрии случайной величины, закон распределения которой симметричен относительно математического ожидания, равен нулю, поскольку в этом случае 
 . Если распределение вероятностей несимметрично, причем «длинная часть» распределения расположена справа от центра группирования, то
. Если распределение вероятностей несимметрично, причем «длинная часть» распределения расположена справа от центра группирования, то  >0 и асимметрию называют положительной, если же «длинная часть» расположена слева, то
>0 и асимметрию называют положительной, если же «длинная часть» расположена слева, то  <0 и асимметрию называют отрицательной.
<0 и асимметрию называют отрицательной.
Вкачестве характеристики большей или меньшей степени «сглаженности» плотности или многоугольника распределения по сравнению с нормальной плотностью используют понятие эксцесса. Эксцессом случайной величины Х называется число, равное разности отношения четвертого центрального момента к четвертой степени среднеквадратического отклонения случайной величины и числа 3:
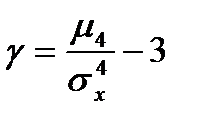 (1.14)
(1.14)
Эксцесс нормального закона распределения вероятностей равен нулю. Если распределение вероятностей случайной величины Х одномодально и плотность распределения  более «островершинна», чем плотность распределения нормальной случайной величины с той же дисперсией, то
более «островершинна», чем плотность распределения нормальной случайной величины с той же дисперсией, то  >0, если же
>0, если же  менее «островершинна» и более «сглажена» по сравнению с плотностью соответствующего нормального распределения, то
менее «островершинна» и более «сглажена» по сравнению с плотностью соответствующего нормального распределения, то  <0.
<0.
В математической статистике широко используются понятия q-квантилей  и Q-процентных точек
и Q-процентных точек  распределения F(x).
распределения F(x).
Квантилью уровня q (или q-квантилью) непрерывной случайной величины Х,обладающей непрерывной функцией распределения F(x), называется такое возможное значение  этой случайной величины, для которого вероятность события Х <
этой случайной величины, для которого вероятность события Х <  равна заданной величине q, т.е.
равна заданной величине q, т.е.  . (1.15)
. (1.15)
|
|
|
Очевидно, чем больше заданное значение q (0< q<1), тем больше будет и соответствующая величина квантили  . Частным случаем квантили - 0.5 –квантилью является характеристика центра группирования - медиана.
. Частным случаем квантили - 0.5 –квантилью является характеристика центра группирования - медиана.
Для дискретной случайной величины функция q -квантиль определяется как любое число  , лежащее между двумя значениями
, лежащее между двумя значениями  и
и  , такими, что
, такими, что  < q, но
< q, но  q.
q.
Под Q-процентной точкой (0< Q <100) случайной величины Х понимается такое ее возможное значение  , для которого вероятность события Х
, для которого вероятность события Х 
 , равна Q/100:
, равна Q/100:
 . (1.16)
. (1.16)
Для дискретной случайной величины это определение корректируется аналогично тому, как это делалось при определении квантилей.
Между квантилями и процентами точками существует следующее соотношение:  .
.
Нормальное распределение (закон Гаусса) занимает центральное место в теории и практике статистических исследований. Распределение задается плотностью:
 , (1.17)
, (1.17)
где  - математическое ожидание;
- математическое ожидание;  - среднеквадратическое отклонение.
- среднеквадратическое отклонение.
Кривая нормального распределения симметрична относительно прямой, параллельной оси ординат и проходящей через точку  , и имеет в этой точке единственный максимум, равный
, и имеет в этой точке единственный максимум, равный  . С уменьшением
. С уменьшением  кривая становится более вытянутой по отношению к прямой
кривая становится более вытянутой по отношению к прямой  . Изменение
. Изменение  при постоянном
при постоянном  не меняет формы кривой, а вызывает лишь ее смещение вдоль оси абсцисс. Таким образом, нормальное распределение зависит от двух параметров:
не меняет формы кривой, а вызывает лишь ее смещение вдоль оси абсцисс. Таким образом, нормальное распределение зависит от двух параметров: 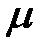 и
и  . Площадь, заключенная под кривой нормального распределения, равна единице. Коэффициент асимметрии и эксцесс равны нулю.
. Площадь, заключенная под кривой нормального распределения, равна единице. Коэффициент асимметрии и эксцесс равны нулю.
Логарифмически-нормальное распределение (логнормальное распределение) – распределение положительной случайной величины, логарифм которой распределен по нормальному закону. Таким образом, если случайная величина Х распределена по нормальному закону, то случайная величина  имеет логнормальное распределение. Распределение является асимметричным.
имеет логнормальное распределение. Распределение является асимметричным.
Плотность вероятности задается следующим выражением:
 . (1.18)
. (1.18)
Математическое ожидание и дисперсия определяются по следующим формулам:
 ; (1.19)
; (1.19)
 , (1.20)
, (1.20)
где  - математическое ожидание Х;
- математическое ожидание Х;  - среднеквадратическое отклонение Х.
- среднеквадратическое отклонение Х.
Биномиальное распределение – распределение вероятностей дискретной случайной величины X=m, принимающей значение 0,1,2,…, n и задаваемой функцией вероятностей:
 , (1.20)
, (1.20)
где  - вероятность появления события А m раз в n независимых испытаниях, в каждом из которых событие А появляется с одно и той же вероятностью p и не появляется с вероятностью
- вероятность появления события А m раз в n независимых испытаниях, в каждом из которых событие А появляется с одно и той же вероятностью p и не появляется с вероятностью  ;
;
 - число сочетаний из n по m.
- число сочетаний из n по m.
Параметрами распределения являются величины n и р. Математическое ожидание и дисперсия задаются следующим образом:
 (1.21)
(1.21)
Равномерное распределение – распределение вероятностей непрерывной случайной величины на каком-либо отрезке  , где
, где  , имеющее плотность:
, имеющее плотность:
 при
при  (1.22)
(1.22)
Математическое ожидание и дисперсия соответственно равны:
 (1.23)
(1.23)
Контрольные вопросы и задачи
1.1. Даны случайные величины X и Y, причем Х=5Y+6. Дисперсия случайной величины Y равна D(Y). Выберите правильное значение D(X):
1) D(Y) 2) 5D(Y) + 6 3) 25 D(Y) 4) D(Y)
1.2. Известно, что M(X)=6, M(Y)=7. Определите М(XY).
1.3. Если эксцесс больше нуля, то:
1) вариационный ряд имеет более крутую вершину по сравнению с нормальной кривой;
2) вариационный ряд имеет более пологую вершину по сравнению с нормальной кривой.
1.4. В результате расчетов определены выборочное среднеквадратическое отклонение s =0,031 и выборочные моменты  = -0,001 и
= -0,001 и  =0,0018. Рассчитайте коэффициент асимметрии и эксцесс.
=0,0018. Рассчитайте коэффициент асимметрии и эксцесс.
1.5. Даны начальные моменты  =3,4;
=3,4;  =11,5;
=11,5;  =40,4;
=40,4;  =144,3. Определите центральные моменты
=144,3. Определите центральные моменты  ,
, 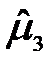 ,
,  .
.
1.6. Медиана является:
1) 0,25 –квантилью 2) 0,5 –квантилью 3) 0,75 -квантилью
Статистическое оценивание
В самом общем смысле статистическое оценивание параметров можно рассматривать как совокупность методов, позволяющих делать научно обоснованные выводы о числовых параметрах генеральной совокупности по случайной выборке из нее.
Генеральной совокупностью называют множество результатов всех мыслимых наблюдений, которые могут быть получены при данном комплексе условий.
Выборочной совокупностью (выборкой) называют множество результатов, случайно отобранных из генеральной совокупности.
Задачи математической статистики практически сводятся к обоснованному суждению об объективных свойствах генеральной совокупности по результатам случайной выборки.
Любая функция θ (Х1 , Х2,…, Хn) от результатов наблюдения Х1 , Х2,…, Хn случайной величины Х называется статистикой.
Статистика  , используемая в качестве приближенного значения неизвестного параметра θ, называется статистической оценкой. Основная задача теории оценивания состоит в том, чтобы произвести выбор оценки
, используемая в качестве приближенного значения неизвестного параметра θ, называется статистической оценкой. Основная задача теории оценивания состоит в том, чтобы произвести выбор оценки  параметра θ, позволяющей получить хорошее приближение оцениваемого параметра.
параметра θ, позволяющей получить хорошее приближение оцениваемого параметра.
Все статистики и статистические оценки являются случайными величинами: при переходе от одной выборки к другой (даже в рамках одной и той же генеральной совокупности) конкретные значения статистической оценки будут подвержены неконтролируемому разбросу. Параметры генеральной совокупности есть постоянные величины.
Методы статистического оценивания состоят из двух больших разделов: точечное оценивание параметров и интервальное оценивание.
Точечной оценкой называют некоторую функцию результатов наблюдения θ (Х1 , Х2,…, Хn), значение которой принимается за наиболее приближенное в данных условиях к значению параметра θ генеральной совокупности. Точечная оценка должна отвечать требованиям состоятельности, несмещенности и эффективности.
Существуют следующие основные методы точечного оценивания случайных величин: метод максимального (наибольшего) правдоподобия; метод моментов; метод наименьших квадратов.
Метод максимального правдоподобия. В соответствии с этим методом оценка  мп неизвестного параметра θ по наблюдениям Х1, Х2,…,Хn случайной величины Х (подчиненной закону распределения f (X,
мп неизвестного параметра θ по наблюдениям Х1, Х2,…,Хn случайной величины Х (подчиненной закону распределения f (X,  ), где f – плотность вероятности) определяется из условия
), где f – плотность вероятности) определяется из условия
L(Х1 , Х2,…, Хn;  мп)=
мп)=  L (Х1 , Х2,…, Хn;
L (Х1 , Х2,…, Хn;  ) (2.1)
) (2.1)
где L – функция правдоподобия.
Если переписать функцию L в виде L = 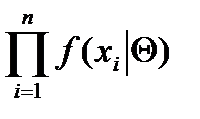 , (2.2)
, (2.2)
тогда логарифм этой функции L =  - (2.3)
- (2.3)
есть логарифмическая функция максимального правдоподобия.
Функция максимального правдоподобия максимизирует количественную оценку  для оценки истинного параметра θ. При этом оценка
для оценки истинного параметра θ. При этом оценка  выбирается таким образом, что реализация функции (2.2) или эквивалентной ей функции (2.3) будет иметь наибольшее значение. Доказано, что оценки максимального правдоподобия являются состоятельными, асимптотически-несмещенными, асимпточески-нормальными и асимптотически-эффективными.
выбирается таким образом, что реализация функции (2.2) или эквивалентной ей функции (2.3) будет иметь наибольшее значение. Доказано, что оценки максимального правдоподобия являются состоятельными, асимптотически-несмещенными, асимпточески-нормальными и асимптотически-эффективными.
Метод моментов. Метод моментов заключается в приравнивании определенного количества выборочных моментов к соответствующим теоретическим (т.е. вычисленным с использованием функции f (X,  )) моментам исследуемой случайной величины, причем последние являются функциями от неизвестных параметров θ(1),…, θ(k). Рассматривая количество моментов, равное числу k подлежащих оценки параметров, и решая полученные уравнения относительно этих параметров, получаются искомые оценки. Доказывается, что оценки неизвестных параметров, полученные методом моментов, являются состоятельными. В силу сравнительно простой вычислительной реализации метод моментов удобен на практике.
)) моментам исследуемой случайной величины, причем последние являются функциями от неизвестных параметров θ(1),…, θ(k). Рассматривая количество моментов, равное числу k подлежащих оценки параметров, и решая полученные уравнения относительно этих параметров, получаются искомые оценки. Доказывается, что оценки неизвестных параметров, полученные методом моментов, являются состоятельными. В силу сравнительно простой вычислительной реализации метод моментов удобен на практике.
Метод наименьших квадратов используется в регрессионном анализе для нахождения оценок параметров уравнения регрессии. Метод состоит в том, чтобы определить оценку неизвестного параметра из решения следующей задачи:

 min, (2.4)
min, (2.4)
где xi – результаты выборочных наблюдений.
Можно показать, что данный функционал достигает своего минимума при таком значении  , при котором обращается в нуль первая производная:
, при котором обращается в нуль первая производная:  .
.
В случае линейных связей, когда наблюдения содержат лишь случайные ошибки (без систематических), оценки, полученные методом наименьших квадратов, являются несмещенными линейными функциями от наблюденных значений. Если ошибки наблюдения независимы и подчиняются нормальному распределению, оценки, полученные данным методом, являются также эффективными.
Несмещенность. Оценка  неизвестного параметра θ называется несмещенной, если при любом объеме выборки n результат ее осреднения по всем возможным выборкам данного объема приводит к точному истинному значению оцениваемого параметра, т.е. М
неизвестного параметра θ называется несмещенной, если при любом объеме выборки n результат ее осреднения по всем возможным выборкам данного объема приводит к точному истинному значению оцениваемого параметра, т.е. М  =θ. (2.5)
=θ. (2.5)
Выполнение требования несмещенности гарантирует отсутствие систематической ошибки в оценке параметра. Разность М  и θ называется смещением оценки.
и θ называется смещением оценки.
Оценканазывается асимптотически несмещенной, если ее смещенность исчезает при условии n  ,т.е. справедливо следующее равенство
,т.е. справедливо следующее равенство
 (М
(М  ) = θ. (2.6)
) = θ. (2.6)
Эффективность. Эффективной оценкой  неизвестного параметра θ называется такая несмещенная оценка, которая обладает наименьшей дисперсией среди всех возможных несмещенных оценок параметра θ для данного объема выборки n.
неизвестного параметра θ называется такая несмещенная оценка, которая обладает наименьшей дисперсией среди всех возможных несмещенных оценок параметра θ для данного объема выборки n.
Данное выше определение опирается на понятие абсолютной эффективности. Несмещенная оценка  являетсяабсолютно эффективной, если она достигает нижнюю границу эффективности, задаваемую неравенством Крамера-Рао.
являетсяабсолютно эффективной, если она достигает нижнюю границу эффективности, задаваемую неравенством Крамера-Рао.
Var 
 M
M  , (2.7)
, (2.7)
где M  -количество информации, содержащейся в выборке.
-количество информации, содержащейся в выборке.  - несмещенная оценка параметра θ, L – функция правдоподобия, Var – знак дисперсии, M – знак математического ожидания.
- несмещенная оценка параметра θ, L – функция правдоподобия, Var – знак дисперсии, M – знак математического ожидания.
Очевидно, что для абсолютно эффективной оценки неравенство (2.7) превращается в равенство. Можно также ввести понятие относительной эффективности.
Для двух несмещенных оценок  1 и
1 и  2 оценка
2 оценка  1 будет более эффективной, если при прочих равных условиях выполняется неравенство:
1 будет более эффективной, если при прочих равных условиях выполняется неравенство:
var( 1) < var(
1) < var( 2) (2.8)
2) (2.8)
Мерой эффективности оценки служит средняя квадратическая ошибка, задаваемая следующей формулой: σ = М{( - θ)2} (2.9)
- θ)2} (2.9)
Оценку  1 называют асимптотически более эффективной, чем оценка
1 называют асимптотически более эффективной, чем оценка  2, если:
2, если:
 var(
var( 1)
1) 
 var(
var( 2) (2.10)
2) (2.10)
Cостоятельность. Оценка  неизвестного параметра θ называется состоятельной, если по мере роста числа наблюдений n (т.е. при n
неизвестного параметра θ называется состоятельной, если по мере роста числа наблюдений n (т.е. при n  ) она стремится по вероятности к оцениваемому значению θ, т.е. если для любого сколь угодно малого ε>0 выполняется условие
) она стремится по вероятности к оцениваемому значению θ, т.е. если для любого сколь угодно малого ε>0 выполняется условие
P 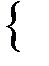
 > ε
> ε 
 . (2.11)
. (2.11)
В теории доказывается, что средняя арифметическая  является несмещенной, состоятельной и эффективной оценкой математического ожидания
является несмещенной, состоятельной и эффективной оценкой математического ожидания  .
.
Выборочная дисперсия  является состоятельной, эффективной, но смещенной оценкой генеральной дисперсии
является состоятельной, эффективной, но смещенной оценкой генеральной дисперсии  . Несмещенной оценкой дисперсии генеральной совокупности будет исправленная выборочная дисперсия
. Несмещенной оценкой дисперсии генеральной совокупности будет исправленная выборочная дисперсия 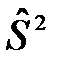 :
:
 =
=  , (2.12)
, (2.12)
где дробь  - является поправкой Бесселя. C ростом
- является поправкой Бесселя. C ростом  поправка стремится к нулю и уже при
поправка стремится к нулю и уже при  >50 практически нет никакой разницы между
>50 практически нет никакой разницы между  и
и  .
.
Законы распределения выборочных характеристик
Распределение Пирсона (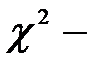 распределение). Если Х1 , Х2,…, Хn есть ряд независимых, нормированных, нормально распределенных случайных величин
распределение). Если Х1 , Х2,…, Хn есть ряд независимых, нормированных, нормально распределенных случайных величин  , т.е.
, т.е. 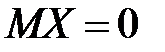 и
и  для
для  , то случайная величина
, то случайная величина
 (2.13)
(2.13)
имеет распределение  с
с  степенями свободы, где
степенями свободы, где  -единственный параметр распределения, характеризующий число случайных величин в выражении ().
-единственный параметр распределения, характеризующий число случайных величин в выражении ().
Математическое ожидание и дисперсия (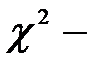 распределения) задаются следующими выражениями:
распределения) задаются следующими выражениями:  (2.14)
(2.14)
Распределение Стьюдента ( - распределение). Если случайная величина Z имеет нормированное нормальное распределение
- распределение). Если случайная величина Z имеет нормированное нормальное распределение  , а величина
, а величина  имеет распределение
имеет распределение  с
с  степенями свободы, причем Z и U взаимно независимы, то случайная величина
степенями свободы, причем Z и U взаимно независимы, то случайная величина
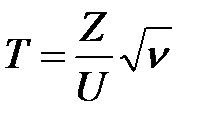 (2.15)
(2.15)
имеет  - распределение с
- распределение с  степенями свободы.
степенями свободы.
Математическое ожидание и дисперсия ( -распределения) задаются следующими выражениями:
-распределения) задаются следующими выражениями: 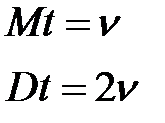 (2.16)
(2.16)
Распределение Фишера-Снедекора. Пусть имеется две независимые случайные величины X и Y, подчиняющиеся нормальному закону распределения. Произведены две независимые выборки объемами 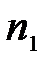 и
и  и вычислены выборочные дисперсии
и вычислены выборочные дисперсии 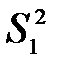 и
и  . Известно, что случайные величины
. Известно, что случайные величины  и
и  имеют распределение
имеют распределение  с соответственно
с соответственно  и
и 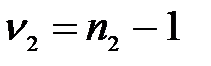 степенями свободы. Случайная величина
степенями свободы. Случайная величина
 (2.17)
(2.17)
имеет F -распределение с  и
и  , причем
, причем  .
.
F -распределение не зависит от неизвестных параметров  и
и  , а зависит от числа наблюдений в выборках
, а зависит от числа наблюдений в выборках 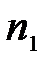 и
и  .
.
Математическое ожидание и дисперсия ( -распределения) задаются следующими выражениями:
-распределения) задаются следующими выражениями: 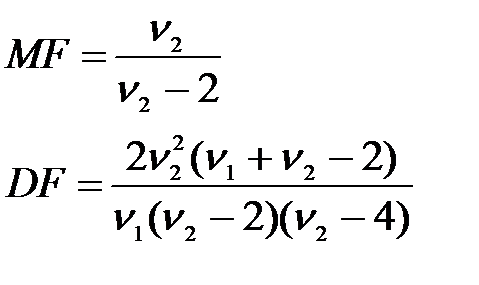 (2.18)
(2.18)
Интервальной оценкой называют доверительный интервал ( -
-  ,
,  +
+  ), определяемый по результатам выборки, относительно которого можно утверждать с определенной, близкой к единице вероятностью, что он заключает в себе истинное значение оцениваемого параметра генеральной совокупности, т.е.
), определяемый по результатам выборки, относительно которого можно утверждать с определенной, близкой к единице вероятностью, что он заключает в себе истинное значение оцениваемого параметра генеральной совокупности, т.е.
Р( -
- 


