 |
Гипотезы о виде законов распределения генеральной совокупности
|
|
|
|
Проверка гипотез о виде законов распределения генеральной совокупности осуществляется с помощью критериев согласия.
Критерием согласия называется статистический критерий, предназначенный для проверки гипотезы Н0 о том, что ряд наблюдений х1, х2,…хn образует случайную выборку, извлеченную из генеральной совокупности Х с функцией распределения F(x)=F(x;θ1; θ2;… θk), где общий вид функции F(x) считается заданным, а параметры θ1; θ2;… θk, от которых она зависит могут быть, как известными, так и неизвестными. Критерии согласия основаны на использовании различных мер расстояний между анализируемой эмпирической функцией распределения Fn(x), определяемой по выборке, и функцией распределения F (x) генеральной совокупности Х.
Математически, нулевую гипотезу можно записать в следующем виде:
Н0: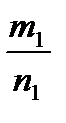 
=р1, 
= р2, 
= р l,
- относительная частота i -го интервала вариационного ряда или i -го варианта, принимаемого случайной величиной Х;
рl – вероятность попадания случайной величины в i-тый интервала или вероятность того, что дискретная величина примет i-тое значение (Х=хi).
Критерий Пирсона (критерий - 
) имеет наибольшее применение при проверке согласования теоретической и эмпирической функций распределения.
Процедура проверки статистической гипотезы о виде распределения с помощью критерия согласия Пирсона состоит из следующих этапов.
1. Весь диапазон значений исследуемой случайной величины разбивается на ряд интервалов группирования Δ1, Δ2, …,Δl, необязательно одинаковой длины.
2. Подсчитывается число точек, попавших в каждый из интервалов группирования Δi.
3. На основе сгруппированных данных вычисляются оценки 
k неизвестных параметров распределения θ k.
|
|
|
4. Вычисляется вероятность рi попадания случайной величины Х в каждый из интервалов группирования Δi.
5. Вычисляется наблюдаемое значение статистики критерия
= 
, (3.32)
сравнивается с табличным значением 
, найденным для уровня значимости α и числа степеней свободы ν = l-k-1, где l -число интервалов, k – число параметров, которыми определяется функция распределения.
Если 
, то гипотеза о том, что генеральная совокупность Х подчиняется закону распределения F (x) принимается.
В случае нормального закона распределения вероятность попадания случайной величины Х в соответствующие интервалы вычисляется по интегральной теореме Лапласа: рi = Р(аi<x<bi) = 
, (3.33)
где t 1i = 
, t 2i = 
; аi,bi – нижняя и верхняя граница соответствующего интервала i.
Контрольные вопросы и задачи
3.1. По результатам 15 испытаний установлено, что среднее время изготовления детали 
= 28с. В предположении, что время изготовления детали является нормальной случайной величиной с известным генеральным средним квадратическим отклонением 
=1,2с, на уровне значимости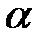 
=0,05 проверить гипотезу Н0: μ= 30 с против конкурирующей гипотезы Н1: μ= 25с.
3.2. На основании 20 измерений, было установлено что средняя длина трубы равна = 15,4м, а s =0,23м. В предположении о нормальном законе распределения на уровне значимости 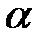=0,05 проверить гипотезу Н0: μ= 15м против конкурирующей гипотезы Н1: μ 
15м.
3.3. По данным задачи 3.2 проверить на уровне значимости 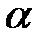=0,05 гипотезу Н0: 
= 0,06 м2 при конкурирующей гипотезе Н1: =0,03 м2.
3.4. По двум независимым выборкам объемом 
n1 =30 и n2 =15, извлеченным из нормальных генеральных совокупностей, найдены выборочные средние 
=25 и 
=27. Дисперсии генеральных совокупностей известны 
=1,3 и 
=1,6. На уровне значимости 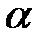=0,1 проверить гипотезу Н0: μ1= μ2 при конкурирующей гипотезе Н1: μ1 
μ2.
3.5. Для сравнения точности изготовления деталей двумя станками-автоматами взяты две выборки объемом n1 =12 и n2 =8. По результатам измерений контролируемого размера деталей вычислены средние =31,5мм и =30,2мм, а также исправленные выборочные дисперсии 
=1,05мм2 и =0,86мм2. Проверить на уровне значимости 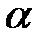=0,05 гипотезу Н0: 
= 
при конкурирующей гипотезе Н1: > .
|
|
|
3.6. По четырем независимым выборкам объемом n1 =12, n2 =8, n3 =13, n4 =11, извлеченным из нормальных генеральных совокупностей, найдены выборочные исправленные дисперсии 
=2,1, 
=1,9, 
=2,2, 
=2,3. Проверить на уровне значимости 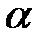=0,05 гипотезу об однородности дисперсий Н0: 
= 
=….= 
.
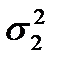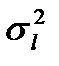3.7. Для сравнения точности работы четырех станков из продукции каждого станка взято по одной выборке из 25 деталей. По результатам измерений найдены несмещенные оценки дисперсий =0,1, =0,19, =0,2, =0,13. Допустив, что погрешность есть нормальная случайная величина, проверить при уровне значимости 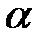=0,05 гипотезу о том, что точность станков одинакова.
3.8. Для сравнения качества работы четырех сборочных конвейеров из общего дневного объема продукции каждого конвейера отобрано соответственно n1 =20, n2 =26, n3 =18, n4 =24 изделий, из которых оказались дефектными m1 =2, m2 =4, m3 =1, m4 =2. На уровне значимости 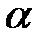=0,05 проверить гипотезу о том, что вероятности появления дефектного изделия на всех станках равны, т.е. Н0: р1= p2 = p3 = p4.
Тема 4. Методика статистического анализа количественных и
качественных показателей
Корреляционный анализ является методом исследования взаимозависимости признаков в генеральной совокупности. Основная задача корреляционного анализа состоит в оценке корреляционной матрицы генеральной совокупности по выборке и определении на ее основе оценок коэффициентов корреляции.
В рамках реализации статистических процедур корреляционного анализа необходимо: выбрать (с учетом специфики и природы анализируемых переменных) подходящий измеритель статистической связи (коэффициент корреляции, корреляционное отношение, ранговый); оценить с помощью точечной и интервальной оценок его числовое значение по выборочным данным; проверить гипотезу о том, что полученное числовое значение анализируемого измерителя связи действительно свидетельствует о наличии статистической связи.
Парная корреляция занимается изучением характеристик взаимосвязи двух случайных величин. Корреляционная зависимость двух случайных величин задается моделью X=X(Y,Z) и Y= Y(Х,Z), где Z –набор внешних случайных факторов.
|
|
|
Основой получения этих характеристик служит совместное распределение случайных величин F(x,y) = P 
.
Плотность двумерного нормального закона распределения определяется пятью параметрами: 
- математическое ожидание Х; 
- математическое ожидание Y; 
- дисперсия Х; 
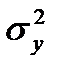- дисперсия Y; 
- парный коэффициент корреляции между Х и Y.
Парный коэффициент корреляции характеризует тесноту линейной связи между двумя переменными. Выборочное значение 
парного коэффициента корреляции ρ подсчитывается по исходным статистическим данным по формуле:
. (4.1)
Коэффициент корреляции не имеет размерности и изменяется в диапазоне
-1 
ρ +1. Положительность коэффициента корреляции означает одинаковый характер тенденции взаимосвязанного изменения случайных величин Х и Y: с увеличением Х наблюдается тенденция увеличения соответствующих индивидуальных значений Y. Отрицательное значение говорит о противоположной тенденции взаимосвязанного изменения случайных величин Х и Y. Если ρ=0, можно сделать вывод, что линейная связь между Х и Y отсутствует. Однако это не означает, что Х и Y статистически независимы, так как не отрицается возможность существования нелинейной связи между Х и Y. Значение ρ= 
говорит о функциональном характере связи между Х и Y.
В рамках корреляционного анализа можно построить линии условных математических ожиданий (линий регрессии у по х и х по у)
у(х)=М(Y/X=x), x(y)=М(X/Y=y); (4.2)
|
|
|
