 |
А также линии условных дисперсий, которые характеризует, насколько точно линии регрессии передают изменение одной случайной величины при изменении другой,
|
|
|
|
 = М
= М  , (4.3)
, (4.3)
 = М
= М  .
.
Точные (или приближенные) прямолинейные регрессии
y(x) =  ,
,  x(y) =
x(y) =  (4.4)
(4.4)
задаются следующими коэффициентами:
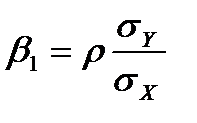 ;
;  , (4.5)
, (4.5)
 ,
,  .
.
Если случайные величины Х и Y независимы, ρ=0, то все условные математические ожидания и дисперсии не зависят от фиксированного значения другой случайной величины и совпадают с безусловными.
Стоит отметить, что выборочные коэффициенты корреляции могут быть формально вычислены для любой двумерной системы наблюдений.
Для проверки значимости парного коэффициента корреляции выдвигается гипотеза Н0: ρ=0. При проверки нулевой гипотезы используется статистика:
 , (4.6)
, (4.6)
имеющая распределение Стьдента с ν=n-2 числом степеней свободы.
Если  <
<  , нулевая гипотеза не отвергается, следовательно, случайные величины Х и Y независимы. Если
, нулевая гипотеза не отвергается, следовательно, случайные величины Х и Y независимы. Если  >
>  , коэффициент корреляции считается значимым.
, коэффициент корреляции считается значимым.
На практике для проверки нулевой гипотезы пользуются также распределением Фишера-Йетса. На уровне значимости α по таблице распределения Фишера-Йетса находят  (α, ν=n-2). Если
(α, ν=n-2). Если 

 , гипотеза отвергается, коэффициент корреляции считается значимым.
, гипотеза отвергается, коэффициент корреляции считается значимым.  - взятое по модулю значение выборочного коэффициента корреляции.
- взятое по модулю значение выборочного коэффициента корреляции.
Для значимых параметров связи можно построить интервальную оценку.
При определении границ доверительного интервала коэффициента корреляции ρ используется преобразование Фишера:  . (4.7)
. (4.7)
Предварительно устанавливают интервальную оценку для 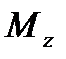 из условия:
из условия:
Р( ) =
) =  =Ф(
=Ф( ), (4.8)
), (4.8)
где  находят по таблице интегральной функции Лапласа для данного уровня
находят по таблице интегральной функции Лапласа для данного уровня  .
.
Получив доверительный интервал для  ,
,  , при помощи таблицы z- преобразования Фишера делают обратный переход от
, при помощи таблицы z- преобразования Фишера делают обратный переход от  и
и  к
к  и
и  . Таким образом окончательно получаем:
. Таким образом окончательно получаем: 

 .
.
При выборе  и
и  следует учитывать нечетность z- функции.
следует учитывать нечетность z- функции.
|
|
|
Трехмерная корреляционная модель является частным случаем множественной корреляционной модели. На примере анализа трехмерной корреляционной модели удобно показать все свойства множественной корреляции. Трехмерная нормально распределенная генеральная совокупность, образуемая тремя признаками X, Y, Z, определяется девятью параметрами: тремя математическими ожиданиями, тремя дисперсиями и тремя парными коэффициентами корреляции:
 ,
,  ,
,  - математические ожидания Х, Y и Z соответственно;
- математические ожидания Х, Y и Z соответственно;
 ,
, 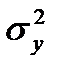 ,
,  - дисперсии Х, Y и Z соответственно;
- дисперсии Х, Y и Z соответственно;
 - парный коэффициент корреляции между Х и Y,
- парный коэффициент корреляции между Х и Y,
 - парный коэффициент корреляции между Х и Z,
- парный коэффициент корреляции между Х и Z,
 - парный коэффициент корреляции между Z и Y.
- парный коэффициент корреляции между Z и Y.
При изучении корреляционной зависимости между более чем двумя случайными величинами с заданным совместным многомерным распределением используют множественные и частные коэффициенты корреляции.
Частный коэффициент корреляции – это мера линейной зависимости между двумя случайными величинами из некоторой совокупности Х1 , Х2,…, Хn, когда исключено влияние остальных случайных величин. Частный коэффициент корреляции обладает всеми свойствами парного коэффициента корреляции. В общем случае частный коэффициент корреляции выражается через элементы корреляционной матрицы R =  , составленной из коэффициентов парной корреляции.
, составленной из коэффициентов парной корреляции.
В рамках простой трехмерной корреляционной модели могут быть рассчитаны три частных коэффициента корреляции:
 ;
;  ;
;  . (34.9)
. (34.9)
Для проверки значимости частного коэффициента корреляции выдвигается гипотеза Н0:  =0. При проверки нулевой гипотезы используется статистика:
=0. При проверки нулевой гипотезы используется статистика:
 , ((34.10)
, ((34.10)
имеющая распределение Стьюдента с ν=n-3 числом степеней свободы.
Если  <
<  , нулевая гипотеза не отвергается, следовательно, случайные величины Х и Y независимы. Если
, нулевая гипотеза не отвергается, следовательно, случайные величины Х и Y независимы. Если  >
>  , коэффициент корреляции считается значимым.
, коэффициент корреляции считается значимым.
Как и в случае парной корреляции на практике для проверки нулевой гипотезы чаще пользуются распределением Фишера-Йейтса. На уровне значимости α по таблице распределения Фишера-Йейтса находят  (α, ν=n-3). Если
(α, ν=n-3). Если 

 , гипотеза отвергается, частный коэффициент корреляции считается значимым.
, гипотеза отвергается, частный коэффициент корреляции считается значимым.  - взятое по модулю значение выборочного частного коэффициента корреляции.
- взятое по модулю значение выборочного частного коэффициента корреляции.
|
|
|
При определении границ доверительного интервала коэффициента корреляции ρ используется преобразование Фишера: 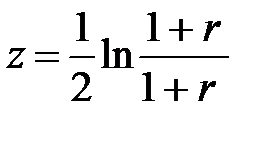 (34.11)
(34.11)
Предварительно устанавливают интервальную оценку для 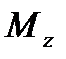 из условия:
из условия:
Р( ) =
) =  =Ф(
=Ф( ), (34.12)
), (34.12)
где  находят по таблице интегральной функции Лапласа для данного уровня
находят по таблице интегральной функции Лапласа для данного уровня  .
.
Получив доверительный интервал для  ,
,  , при помощи таблицы z- преобразования Фишера делают обратный переход от
, при помощи таблицы z- преобразования Фишера делают обратный переход от  и
и  к
к  и
и  . Таким образом окончательно получаем:
. Таким образом окончательно получаем: 

 .
.
Множественный коэффициент корреляции R служит мерой линейной зависимости между случайной величиной Х1 и набором случайных величин Х2,…, Хn. В общем случае множественные коэффициенты корреляции выражаются через элементы корреляционной матрицы. Для трехмерной модели может быть рассчитано три множественных коэффициента корреляции:
 ;
;
 ; (34.13)
; (34.13)
 .
.
Множественный коэффициент корреляции изменяется в диапазоне 0  R
R  +1. Если, например,
+1. Если, например,  = 1, то связь между случайной величиной Х и двумерной случайной величиной (Х,Z) является функциональной; если
= 1, то связь между случайной величиной Х и двумерной случайной величиной (Х,Z) является функциональной; если  = 0, то случайная величина Х и двумерная случайная величина (Х,Z) независимы.
= 0, то случайная величина Х и двумерная случайная величина (Х,Z) независимы.
Множественный коэффициент детерминации  показывает долю дисперсии случайной величины Х1, обусловленную влиянием остальных факторов Х2,…, Хn, входящих в многомерную модель. Множественный коэффициент детерминации может увеличиваться при введении в модель дополнительных признаков и не увеличиваться при исключении некоторых признаков из модели. Для двухмерной корреляционной модели коэффициент детерминации равен квадрату парного коэффициента корреляции.
показывает долю дисперсии случайной величины Х1, обусловленную влиянием остальных факторов Х2,…, Хn, входящих в многомерную модель. Множественный коэффициент детерминации может увеличиваться при введении в модель дополнительных признаков и не увеличиваться при исключении некоторых признаков из модели. Для двухмерной корреляционной модели коэффициент детерминации равен квадрату парного коэффициента корреляции.
При проверке значимости множественного коэффициента корреляции (множественного коэффициента детерминации) выдвигается гипотеза Н0: 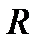 =0 (или
=0 (или  =0). При проверке нулевой гипотезы используется статистика:
=0). При проверке нулевой гипотезы используется статистика:
 , (34.14)
, (34.14)
имеющая распределение Фишера-Снедекора с числом степеней свободы  =2 и
=2 и  n-2.
n-2.
Если  (α,
(α,  ,
, 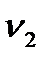 ), нулевая гипотеза отвергается, следовательно, множественный коэффициент корреляции (множественный коэффициент детерминации) считается значимым.
), нулевая гипотеза отвергается, следовательно, множественный коэффициент корреляции (множественный коэффициент детерминации) считается значимым.
|
|
|
Корреляционное отношение. Как уже отмечалось выше коэффициент корреляции является адекватной мерой статистической взаимозависимости только в случае линейного характера связи между признаками. Для изучения связи между признаками, выражаемой нелинейной функцией, применяется более общий показатель тесноты связи – корреляционное отношение. В теории статистики разработан специальный критерий оценки нелинейности связи между двумя переменными:
 , (34.15)
, (34.15)
где  - корреляционное отношение между X и Y,
- корреляционное отношение между X и Y,
 - коэффициент корреляции между X и Y.
- коэффициент корреляции между X и Y.
Если  >2,5, то корреляционную связь можно считать нелинейной.
>2,5, то корреляционную связь можно считать нелинейной.
Использование корреляционного отношения основано на разложении общей дисперсии зависимой переменной на составляющие: дисперсию, характеризующую влияние объясняющей переменной, и дисперсию, характеризующую влияние неучтенных факторов:  , (34.16)
, (34.16)
где 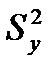 - общая дисперсия зависимой переменной,
- общая дисперсия зависимой переменной,
 - дисперсия функции регрессии относительно среднего значения зависимой переменной, характеризующая влияние объясняющей переменной.
- дисперсия функции регрессии относительно среднего значения зависимой переменной, характеризующая влияние объясняющей переменной.
 - остаточная дисперсия.
- остаточная дисперсия.
Корреляционное отношение определяется по формуле:
 =
=  (34.17)
(34.17)
Корреляционное отношение не имеет размерности и изменяется в диапазоне 0 

 +1.
+1.
Для проверки значимости корреляционного отношения выдвигается гипотеза Н0:  =0. При проверке нулевой гипотезы используется статистика:
=0. При проверке нулевой гипотезы используется статистика:
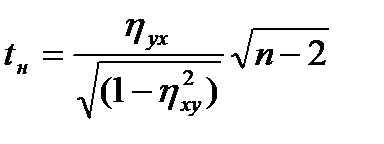 , (43.18)
, (43.18)
которая имеет распределение Стьюдента с числом степеней свободы ν=n-2. Если  <
<  , нулевая гипотеза не отвергается, следовательно, случайные величины Х и Y независимы. Если
, нулевая гипотеза не отвергается, следовательно, случайные величины Х и Y независимы. Если  >
>  , коэффициент корреляции считается значимым.
, коэффициент корреляции считается значимым.
Доверительный интервал имеет вид:  , (34.19)
, (34.19)
где  находят по таблице интегральной функции Лапласа для данного уровня
находят по таблице интегральной функции Лапласа для данного уровня  .
.
Ранговая корреляция. Для изучения взаимосвязи признаков, не поддающихся количественному измерению, используются различные показатели ранговой корреляции. Под ранговой корреляцией понимается статистическая связь между порядковыми переменными. В статистической практике эта связь анализируется на основании исходных статистических данных, представленных упорядочениями (ранжировками) n рассматриваемых объектов. Методы ранговой корреляции широко используются, в частности, при организации и статистической обработке различного рода систем экспертных обследований.
|
|
|
Для измерения тесноты связи между порядковыми переменными используются различные показатели, такие как коэффициент Спирмена, коэффициент Кэнделла, коэффициенты конкордации, ассоциации, контингенции.
Рассмотрим пример расчета рангового коэффициента корреляции Спирмена.
 , (34.20)
, (34.20)
где  - разность значений рангов, расположенных в двух рядах у одного и того же объекта.
- разность значений рангов, расположенных в двух рядах у одного и того же объекта.
Если два ряда полностью совпадают, то  =0, и следовательно,
=0, и следовательно,  =1. При полной обратной связи ранги двух рядов расположены в обратном порядке и
=1. При полной обратной связи ранги двух рядов расположены в обратном порядке и  =-1. При отсутствии корреляции между рангами
=-1. При отсутствии корреляции между рангами  =0.
=0.
Для проверки значимости рангового коэффициента корреляции Спирмена выдвигается гипотеза Н0:  =0. При проверке нулевой гипотезы вычисляется критическая точка:
=0. При проверке нулевой гипотезы вычисляется критическая точка:  , (43.21)
, (43.21)
где  определяется по таблице распределения Стьюдента для уровня значимости α и числа степеней свободы ν=n-2. Если
определяется по таблице распределения Стьюдента для уровня значимости α и числа степеней свободы ν=n-2. Если  нулевая гипотеза не отвергается, следовательно, случайные величины Х и Y независимы. В противном случае ранговый коэффициент корреляции считается значимым.
нулевая гипотеза не отвергается, следовательно, случайные величины Х и Y независимы. В противном случае ранговый коэффициент корреляции считается значимым.
Регрессионный анализ – статистический метод исследования зависимости случайной величины Y от переменных Х1 , Х2,…, Хm, рассматриваемых как неслучайные величины, независимо от истинного закона распределения Хi.
Регрессия – функция f (Х1 , Х2,…, Хm), описывающая зависимость условного математического ожидания зависимой переменной Y (вычисленного при условии, что независимые переменные зафиксированы на уровнях Х1 , Х2,…, Хm) от заданных фиксированных значений независимых переменных.
В рамках регрессионного анализа решаются следующие задачи: выбор математической модели, описывающей изучаемый процесс; отбор наиболее информативных объясняющих переменных (регрессоров); вычисление оценок для неизвестных значений параметров, участвующих в записи уравнения искомой зависимости; анализ точности полученного уравнения связи.
Выбор конкретной формы уравнения регрессии зависит от экономической сущности изучаемого явления или процесса. На практике чаще всего встречаются следующие виды уравнений регрессии:
1) 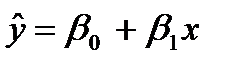 - двумерное линейное;
- двумерное линейное;
2)  - многомерной линейное;
- многомерной линейное;
3)  - полиномиальное;
- полиномиальное;
4)  - гиперболическое;
- гиперболическое;
5)  - степенное.
- степенное.
Так как аппарат исследования линейных функций разработан наиболее полно, на практике чаще всего прибегают к линейному преобразованию (линеаризации) степенных, полиномиальных, гиперболических, а также любых других нелинейных функций, поддающихся такому преобразованию. Например, степенное регрессионное уравнение может быть приведено к линейной форме путем логарифмирования:
|
|
|
 ,
,
и далее
 ,
,
где  = lg
= lg  ,
,  = lg
= lg  ,
,  =
=  .
.
Общая модель линейной относительно оцениваемых параметров регрессии может быть представлена следующим образом:
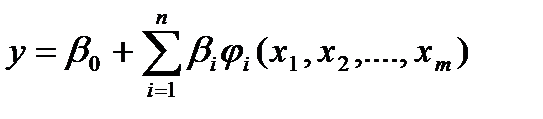 +ε,
+ε,
где  - некоторая функция переменных
- некоторая функция переменных  ,
,
 - неизвестные параметры уравнения регрессии, которые необходимо оценить по выборочным данным,
- неизвестные параметры уравнения регрессии, которые необходимо оценить по выборочным данным,
 - случайное слагаемое или ошибка модели (возмущение), с нулевым математическим ожиданием
- случайное слагаемое или ошибка модели (возмущение), с нулевым математическим ожиданием 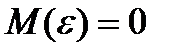 и дисперсией
и дисперсией  .
.
Для оценки неизвестных параметров модели используются уже описанные выше статистические методы оценивания: метод максимального правдоподобия (ММП), метод наименьших квадратов (ММП) и метод моментов. В теории регрессионного анализа доказывается, что ММП– и МНК–оценки являются наилучшими линейными оценками неизвестных параметров уравнения регрессии, обладающими свойствами несмещенности и эффективности.
Ввиду относительной простоты реализации в практических приложениях чаще всего используется метод наименьших квадратов. Для получения несмещенных и эффективных МНК-оценок неизвестных параметров необходимо выполнение некоторых предпосылок, касающихся как всего уравнения в целом, так и его отдельных составляющих.
Основные предпосылки формулируются следующим образом:
1. Объем наблюдений n больше числа оцениваемых параметров m.
2. Между объясняющими переменными не должно существовать строгой линейной зависимости, т.е. предполагается отсутствие мультиколлинеарности.
3. Зависимая переменная Y и объясняющие параметры Хi распределены нормально.
4. Регрессоры являются неслучайными величинами.
5. При построении функции регрессии предполагается, что результативный признак Y зависит только от объясняющих переменных Хi, которые включены в регрессию. Таким образом, предполагается, что на переменную Y не оказывают влияния никакие другие систематически действующие факторы. Суммарный эффект от воздействия на зависимую переменную неучтенных факторов учитывается возмущающей переменной ε. При этом предполагается, что математическое ожидание возмущающей переменной ε равно 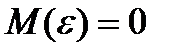 .
.
6. Объясняющие переменные не коррелируют с возмущающей переменной ε, т.е.  =0. Отсюда следует, что переменные Хi объясняют переменную Y, а переменная Y не объясняет переменные Хi.
=0. Отсюда следует, что переменные Хi объясняют переменную Y, а переменная Y не объясняет переменные Хi.
7. Распределение возмущающей переменной подчиняется нормальному закону распределения.
8. Возмущающая переменная ε имеет постоянную дисперсию  . Это свойство возмущающей переменной называется гомоскедастичностью.
. Это свойство возмущающей переменной называется гомоскедастичностью.
9. Значения возмущающей переменной ε попарно некоррелированы, т.е.  для s ≠0. Иначе это свойство называется отсутствием автокорреляции возмущающей переменной ε.
для s ≠0. Иначе это свойство называется отсутствием автокорреляции возмущающей переменной ε.
Для нахождения оценок неизвестных параметров  и
и  двумерного линейного уравнения регрессии
двумерного линейного уравнения регрессии  используется метод наименьших квадратов. В соответствии с МНК оценки
используется метод наименьших квадратов. В соответствии с МНК оценки  и
и  можно получить из условия минимизации суммы квадратов ошибок оцениваемых параметров, т.е. суммой квадратов отклонений фактических значений зависимой переменной от ее расчетных значений, полученных на основе уравнения регрессии:
можно получить из условия минимизации суммы квадратов ошибок оцениваемых параметров, т.е. суммой квадратов отклонений фактических значений зависимой переменной от ее расчетных значений, полученных на основе уравнения регрессии:
 , (4.22)
, (4.22)
где  и
и  - оценки неизвестных параметров
- оценки неизвестных параметров  и
и  соответственно;
соответственно;
 - расчетные значения зависимой переменной
- расчетные значения зависимой переменной  .
.
Разность  называется остатком и дает количественную оценку воздействия возмущающей переменной ε.
называется остатком и дает количественную оценку воздействия возмущающей переменной ε.
Дифференцируя функционал S по  и
и  и приравнивая нулю частные производные, получаем следующую систему уравнений:
и приравнивая нулю частные производные, получаем следующую систему уравнений:
 (4.23)
(4.23)
После соответствующих преобразований имеем:
 (4.24)
(4.24)
Решив данную систему относительно  и
и  , окончательно получим:
, окончательно получим:
 ; (4.25)
; (4.25)
 . (4.26)
. (4.26)
Свободный член уравнения регрессии  определяет точку пересечения линии регрессии с осью ординат.
определяет точку пересечения линии регрессии с осью ординат.  является средним значением Y в точке Х=0 и задает масштаб изменения зависимой переменной Y. Коэффициент
является средним значением Y в точке Х=0 и задает масштаб изменения зависимой переменной Y. Коэффициент  имеет размерность зависимой переменной. Его экономическая интерпретация очень затруднительна или вообще невозможна. Коэффициент
имеет размерность зависимой переменной. Его экономическая интерпретация очень затруднительна или вообще невозможна. Коэффициент  показывает среднюю величину изменения зависимой переменной Y при изменении объясняющей переменной Х на одну единицу своего измерения. Знак при
показывает среднюю величину изменения зависимой переменной Y при изменении объясняющей переменной Х на одну единицу своего измерения. Знак при  показывает направление изменения. При положительном коэффициенте регрессии увеличение значений объясняющей переменной ведет к увеличению значений зависимой переменной. При отрицательном коэффициенте увеличение значений объясняющей переменной ведет к убыванию значений зависимой переменной.
показывает направление изменения. При положительном коэффициенте регрессии увеличение значений объясняющей переменной ведет к увеличению значений зависимой переменной. При отрицательном коэффициенте увеличение значений объясняющей переменной ведет к убыванию значений зависимой переменной.
После нахождения оценок  и
и  неизвестных параметров
неизвестных параметров  и
и  необходимо осуществить проверку значимости параметров регрессии и всего уравнения в целом, а также построить доверительные интервалы для оцениваемых параметров и интервал прогнозирования для независимой переменной.
необходимо осуществить проверку значимости параметров регрессии и всего уравнения в целом, а также построить доверительные интервалы для оцениваемых параметров и интервал прогнозирования для независимой переменной.
Для проверки значимости уравнения регрессии в случае двумерной модели выдвигается гипотеза Н0:  =0. В основе проверки лежит идея дисперсионного анализа, состоящая в разложении дисперсии на составляющие. Общая сумма Sобщ квадратов отклонений зависимой переменной разлагается на сумму квадратов SR отклонений, обусловленных регрессией, которая характеризует воздействие объясняющей переменной, и сумму квадратов Sост отклонений относительно плоскости регрессии, характеризующую воздействие неучтенных в модели факторов.
=0. В основе проверки лежит идея дисперсионного анализа, состоящая в разложении дисперсии на составляющие. Общая сумма Sобщ квадратов отклонений зависимой переменной разлагается на сумму квадратов SR отклонений, обусловленных регрессией, которая характеризует воздействие объясняющей переменной, и сумму квадратов Sост отклонений относительно плоскости регрессии, характеризующую воздействие неучтенных в модели факторов.
Sобщ = SR + Sост, (4.27)
где Sобщ =  ; SR =
; SR =  ; Sост
; Sост  .
.
Проверка гипотеза основана на критерии  , (4.28)
, (4.28)
имеющем распределение Фишера-Снедекора.
Нулевая гипотеза отвергается, если 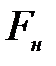 оказывается больше, чем значение
оказывается больше, чем значение  , найденное для уровня значимости α и числа степеней свободы
, найденное для уровня значимости α и числа степеней свободы  =2 и
=2 и  n-2. В противном случае гипотеза принимается.
n-2. В противном случае гипотеза принимается.
Стоит отметить, что только для частного случая двумерной модели проверка значимости уравнения регрессии фактически сводится к проверке значимости единственного коэффициента регрессии  (проверка значимости свободного члена, как правило, не проводится). В случае же многомерной модели, необходимо проверять как значимость отдельных коэффициентов, так и всего уравнения.
(проверка значимости свободного члена, как правило, не проводится). В случае же многомерной модели, необходимо проверять как значимость отдельных коэффициентов, так и всего уравнения.
Используя значение Sост, можно получить оценку остаточной дисперсии  по формуле:
по формуле:  . (4.29)
. (4.29)
Остаточная дисперсия является одной из важных характеристик качества регрессионной модели. Чем меньше значение  , тем ближе расчетные значения к фактическим, и, следовательно, тем точнее модель описывает изучаемый процесс.
, тем ближе расчетные значения к фактическим, и, следовательно, тем точнее модель описывает изучаемый процесс.
Еще одним важным показателем качества регрессионной модели является коэффициент детерминации, который для двухмерной рассчитывается по формуле:
 . (4.30)
. (4.30)
Если уравнение регрессии значимо, то представляет интерес определение с надежностью γ доверительных интервалов для  ,
,  и
и  .
.
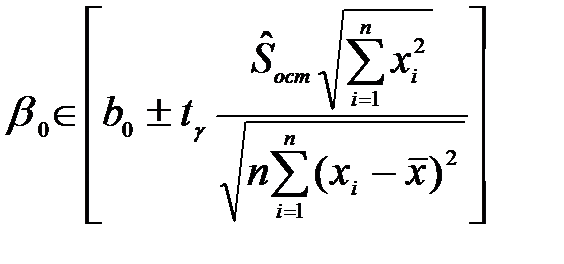 ; (4.31)
; (4.31)
 ; (4.32)
; (4.32)
 . (4.33)
. (4.33)
где  определяется по таблице распределения Стьюдента для уровня значимости α=1-γ и числа степеней свободы
определяется по таблице распределения Стьюдента для уровня значимости α=1-γ и числа степеней свободы 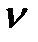 =2;
=2;  - заданное значение Х, для которого находится интервальная оценка параметра
- заданное значение Х, для которого находится интервальная оценка параметра  .
.
Доверительную оценку для интервала предсказания в точке Х= х0 определяют из условия  , (4.34)
, (4.34)
где  определяется по таблице распределения Стьюдента для уровня значимости α=1-γ и числа степеней свободы
определяется по таблице распределения Стьюдента для уровня значимости α=1-γ и числа степеней свободы 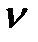 =n-2.
=n-2.
На практике для сравнительного анализа влияния разных факторов, входящих в регрессионную модель, используют коэффициенты эластичности и стандартизованные  - коэффициенты. Их применение помогает устранить различие в единицах измерения объясняющих переменных. В многомерных моделях с большим количеством регрессоров с помощью данных коэффициентов можно ранжировать объясняющие переменные по степени их относительного влияния на зависимую переменную.
- коэффициенты. Их применение помогает устранить различие в единицах измерения объясняющих переменных. В многомерных моделях с большим количеством регрессоров с помощью данных коэффициентов можно ранжировать объясняющие переменные по степени их относительного влияния на зависимую переменную.
Коэффициент эластичности вычисляется по формуле:  . (4.35)
. (4.35)
и показывает, на сколько процентов в среднем изменится результативный признак, если факторный признак (объясняющая переменная) увеличится на один процент при условии, что все другие факторные признаки равны своим средним значениям.
Стандартизованные коэффициенты  помогают устранить различия в степени колеблемости объясняющих переменных:
помогают устранить различия в степени колеблемости объясняющих переменных:  =
=  . (4.36)
. (4.36)
Величина  показывает, на сколько среднеквадратических отклонений изменится зависимая переменная при изменении объясняющей переменной на одно среднеквадратическое отклонение.
показывает, на сколько среднеквадратических отклонений изменится зависимая переменная при изменении объясняющей переменной на одно среднеквадратическое отклонение.
Множественная линейная модель. Для оценки неизвестных параметров линейной многомерной модели методом наименьших квадратов используется аппарат матричной алгебры.
В матричной форме уравнение  имеет вид
имеет вид  ,
,
где  - вектор-столбец наблюдений размерности n;
- вектор-столбец наблюдений размерности n;




 - матрица факторных признаков размерности (n
- матрица факторных признаков размерности (n  (m+1));
(m+1));
 - вектор неизвестных параметров размерности (m +1).
- вектор неизвестных параметров размерности (m +1).
Оценка наименьших квадратов вектора  имеет вид
имеет вид
 , (4.37)
, (4.37)
где  - вектор-столбец оценок размерности (m +1);
- вектор-столбец оценок размерности (m +1);
 - транспонированная матрица Х;
- транспонированная матрица Х;
 - матрица, обратная матрице
- матрица, обратная матрице  .
.
Вектор  является несмещенной оценкой
является несмещенной оценкой  , т.е.
, т.е.  .
.
Дисперсия оценки  определяется из выражения
определяется из выражения

 , (4.38)
, (4.38)
где  - диагональной элемент матрицы
- диагональной элемент матрицы  , соответствующий
, соответствующий
l -строке и l -столбцу, l=  +1.
+1.
Значимость уравнения регрессии, т.е. гипотеза  , проверяется с помощью критерия, основанного на статистике:
, проверяется с помощью критерия, основанного на статистике:  , (4.39)
, (4.39)
имеющей распределение Фишера-Снедекора с числом степеней свободы  =m+1 и
=m+1 и  n – m – 1,
n – m – 1,
где  - сумма квадратов отклонений, обусловленных регрессией;
- сумма квадратов отклонений, обусловленных регрессией;
 - сумма квадратов отклонений, характеризующая воздействие неучтенных в модели факторов.
- сумма квадратов отклонений, характеризующая воздействие неучтенных в модели факторов.
Нулевая гипотеза отвергается, если 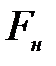 оказывается больше чем
оказывается больше чем  , найденное для уровня значимости α и числа степеней свободы
, найденное для уровня значимости α и числа степеней свободы  и
и  . В противном случае гипотеза принимается.
. В противном случае гипотеза принимается.
Значимость отдельных коэффициентов можно проверить с помощью критерия, основанного на статистике
 , где
, где  =
=  , (4.40)
, (4.40)
имеющей распределение Фишера-Снедекора с числом степеней свободы  =
=  и
и  n – m – 1.
n – m – 1.
Доверительный интервал для параметра  имеет вид:
имеет вид:  , (4.41)
, (4.41)
где  определяется по таблице распределения Стьюдента для уровня значимости α=1-γ и числа степеней свободы
определяется по таблице распределения Стьюдента для уровня значимости α=1-γ и числа степеней свободы 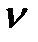 = n – m – 1.
= n – m – 1.
Интервальная оценка для  в точке, определяемой вектором
в точке, определяемой вектором  начальных условий, равна
начальных условий, равна
 , (4.42)
, (4.42)
где  определяется по таблице распределения Стьюдента для уровня значимости α=1-γ и числа степеней свободы
определяется по таблице распределения Стьюдента для уровня значимости α=1-γ и числа степеней свободы 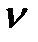 = n – m – 1.
= n – m – 1.
Доверительная оценка для интервала предсказания  определяется как
определяется как
 , (4.43)
, (4.43)
где  определяется по таблице распределения Стьюдента для уровня значимости α=1-γ и числа степеней свободы
определяется по таблице распределения Стьюдента для уровня значимости α=1-γ и числа степеней свободы 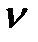 = n – m – 1.
= n – m – 1.
Контрольные вопросы и задачи
41.1. На основании выборочных данных о производительности труда (Y) и средней загрузки мощностей (Х), полученных с однотипных предприятий (табл.1) а) найдите точечную оценку коэффициента корреляции между Х и Y; б) на уровне значимости 
 =0.05 проверьте значимость коэффициента корреляции и в) найдите его интервальную оценку при
=0.05 проверьте значимость коэффициента корреляции и в) найдите его интервальную оценку при  =0.95.
=0.95.
| Х | ||||||||||
| Y |
4.2. На основании полученной выборки n= 30 для трех показателей Х, Y и Z рассчитаны парные коэффициенты корреляции:  =0.91,
=0.91, 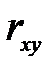 =0.65
=0.65  =0.74. Рассчитайте частные коэффициенты корреляции, проверьте их значимость (
=0.74. Рассчитайте частные коэффициенты корреляции, проверьте их значимость ( =0.05) и постройте для значимых коэффициентов доверительные интервалы (
=0.05) и постройте для значимых коэффициентов доверительные интервалы ( =0.95).
=0.95).
4.3. По данным задачи 4.2 рассчитайте множественны
|
|
|


