 |
С помощью линейных и нелинейных трендов
|
|
|
|
Одной из основных задач изучения динамики процессов внешней торговли является задача выявления тенденций развития этих процессов.
Тенденцию развития любого процесса формируют факторы, условия, которые систематически, в течение длительного периода времени оказывают на него влияние. Таким образом, тенденция динамики связана с действием долговременно существующих, значимых причин и условий развития. По истечении какого-то периода времени эти причины и условия могут измениться и породить уже другую тенденцию развития изучаемого процесса. Поэтому, в разные периоды существования процесса тенденция его развития может быть весьма различной по форме и по степени устойчивости.
Наличие тенденции заметно облегчает задачу предвидения, прогнозирования. Поэтому важно уметь выявить тенденцию, выразить эту тенденцию в аналитической форме – в форме уравнения тренда, оценить тренд и правильно применить его для прогнозирования.
Само понятие тренда как устойчивой, выраженной тенденции развития предполагает способы его выявления. Тренд проявляется при погашении случайных колебаний (отклонений от тренда), которым подвержены уровни любых процессов и явлений, в том числе и внешней торговли.
В наиболее простом виде задачу выявления тенденции решают динамические средние, рассмотренные ранее. Более сложным методом выявления тренда является аналитическое выравнивание, которое позволяет представить тренд в форме уравнения прямой или кривой линии. Для представления процессов внешней торговли наиболее часто используются следующие формы уравнений:
- линейная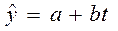 
;
- гиперболическая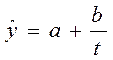 
;
- логарифмическая 
или 
;
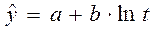- степенная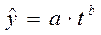 
;
|
|
|
- экспоненциальная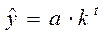 
;
- параболическая второго порядка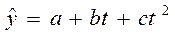 
и другие,
где t – фактор времени,
a - уровень тренда в период (момент), принятый за начало отсчёта времени (t = 0);
b – средний прирост (константа тренда);
с – квадратический параметр тренда, равный половине ускорения (константа тренда);
k – темп изменения в разах (константа тренда).
Построение тренда основано на применении метода наименьших квадратов (МНК), который минимизирует сумму квадратов отклонений фактических уровней временного ряда от теоретических, полученных по
уравнению тренда:
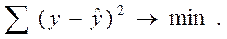
Прежде всего вводится фактор времени t, как натуральный ряд чисел от 1 до n. Затем определяются параметры тренда a и b по общеизвестным
формулам:
(1) 
(2).
Для построения линейного тренда указанные формулы упрощаются, если фактор времени t ввести таким образом, чтобы 
. Тогда форму-
лы для расчёта параметров a и b принимают вид:
При построении нелинейных форм трендов необходимо предварительно провести их линеаризацию, то есть нелинейную форму привести к виду, схожему с линейной формой. Как правило, для этого необходимо прологарифмировать исходную нелинейную функцию и полученные логарифмы обозначить новыми буквенными символами. Например, для построения степенной функции 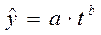логарифмируем её: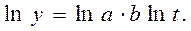 
Далее даём логарифмам новые буквенные обозначения и получаем:
,
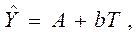то есть функцию в виде, схожем с линейной формой. К полученной функции можно применять формулы (1) и (2).
квадратическое отклонение. Размах вариации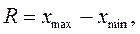 
показывает разницу между наибольшим и наименьшим значениями признака.
Среднее линейное отклонение
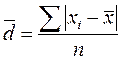
для несгруппированных данных, или
для сгруппированных данных, показывает на какую величину в среднем по совокупности индивидуальные значения признака отличаются от его среднего значения.
Среднее квадратическое отклонение
для несгруппированных данных, или
|
|
|
|
|
|
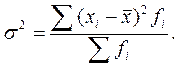
