 |
Краткая теория и методические рекомендации
|
|
|
|
ФОРМАЛИЗАЦИЯ ВЫСКАЗЫВАНИЙ. ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ. УПРОЩЕНИЕ ФОРМУЛ ЛОГИКИ С ПОМОЩЬЮ РАВНОСИЛЬНЫХ ПРЕОБРАЗОВАНИЙ.
ЦЕЛЬ РАБОТЫ: научиться формализовывать высказывания, строить таблицы истинности для формул логики, упрощать формулы логики с помощью равносильных преобразований
Для выполнения работы необходимо знать основные формулы алгебры высказываний, методы минимизации алгебраических преобразований; необходимо уметь формулировать задачи логического характера и применять методы математической логики для их решения.
Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.2.Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности; ПК 1.4. Участвовать в экспериментальном тестировании информационной системы на этапе опытной эксплуатации, фиксировать выявленные ошибки кодирования в разрабатываемых модулях информационной системы.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Формулой алгебры логики называется всякое составное высказывание, содержащее логические переменные и знаки логических операций. Для записи составного высказывания на формальном языке нужно выделить простые высказывания и логические связи между ними.
Пример 1. Записать с помощью формулы логики высказывание: неверно, что если нет дождя, то будет солнечная погода, и дождь пойдет тогда и только тогда, когда будет ветер.
Решение. Обозначим буквой А высказывание: «идет дождь», буквой В высказывание: «будет солнечная погода», буквой С высказывание: «будет ветер». Разделим составное высказывание на простые и каждое запишем с помощью формулы логики:
|
|
|
«нет дождя» - 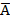 ; «если нет дождя, то будет солнечная погода» -
; «если нет дождя, то будет солнечная погода» -  ;
;
«дождь пойдет тогда и только тогда, когда будет ветер» - 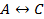 .
.
Между простыми высказываниями стоит союз «и», т.е. они соединяются с помощью конъюнкции и составное высказывание «если нет дождя, то будет солнечная погода, и дождь пойдет тогда и только тогда, когда будет ветер» запишется в виде: 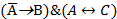 . Т.к. перед этим составным высказыванием стоит слово «неверно», то нужно поставить отрицание над всей формулой.
. Т.к. перед этим составным высказыванием стоит слово «неверно», то нужно поставить отрицание над всей формулой.
В итоге заданное высказывание формализуется следующим образом: 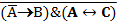 .
.
Ответ: 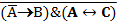 .
.
Для каждого логического выражения можно построить таблицу истинности, позволяющую определить истинность или ложность логического выражения при всех возможных комбинациях исходных значений логических переменных.
Пример 2. Построить таблицы истинности для формулы 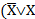 )↔(X®Y&
)↔(X®Y& 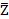 ).
).
Решение. Определим количество строк и столбцов в таблице. Т.к. в логическое выражение входят три переменные, то по формуле 23 получим 8 строк. Количество столбцов равно количеству логических переменных (3) + количество операций (6), получим 9 столбцов. Учитывая приоритет операций, расставляем порядок действий 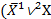 )
) 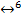 (X
(X  Y
Y  ). Заполняем таблицу:
). Заполняем таблицу:
| X | Y | Z | 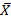
| 
| 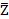
| Y& 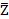
| X®Y& 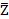
| 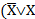 )↔(X®Y& )↔(X®Y& 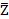 ) )
|
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Формулы алгебры логики называются равносильными, если они принимают одинаковые логические выражения (0 или 1) при одинаковых наборах значений, входящих в них высказываний. Равносильность формул можно доказать с помощью таблиц истинности или методом равносильных (эквивалентных) преобразований, используя основные законы логики. Законы логики также применяются для упрощения формул логики.
|
|
|
Пример 3. С помощью равносильных преобразований упростить формулу логики: (x®y)Ú(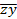 ).
).
Решение. 1. Используя формулу: x®y=  Úy, избавимся от операции импликации: (x®y)Ú(
Úy, избавимся от операции импликации: (x®y)Ú(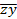 ) = (
) = ( Úy)Ú(
Úy)Ú(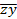 ).
).
2. Используя закон де Моргана 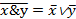 , преобразуем вторую скобку: (
, преобразуем вторую скобку: ( Úy)Ú(
Úy)Ú(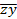 ) = (
) = ( Úy)Ú(
Úy)Ú(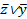 )
)
3. Используя законы коммутативности и ассоциативности, сгруппируем слагаемые следующим образом: ( Úy)Ú(
Úy)Ú(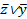 ) = (
) = ( .
.
4. По закону исключенного третьего 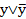 =1, т.е. (
=1, т.е. ( =
=  .
.
Таким образом, решение данного примера будет следующим:
(x ® y) Ú ( 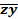 ) = (
) = (  Ú y) Ú (
Ú y) Ú ( 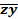 ) = (
) = (  Ú y) Ú (
Ú y) Ú ( 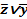 ) = (
) = ( 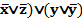 =
= 
Ответ: (x ® y) Ú( 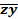 ) =
) = 
|
|
|


