 |
Порядок выполнения работы и форма отчетности
|
|
|
|
Задание 1.
Записать высказывания с помощью формулы логики.
| I вариант | II вариант | III вариант |
| Если светит солнце и не дует ветер, то не будет дождя | Если дует ветер, то солнце светит тогда и только тогда, когда нет дождя | Погода будет солнечной тогда и только тогда, когда ни будет ни ветра, ни дождя |
| IV вариант | V вариант | VI вариант |
| Неверно, что если дует ветер и солнце светит, то нет дождя | Если ветра нет, то дождь будет тогда и только тогда, когда будет пасмурная погода | Неверно, что если погода пасмурная, то дождь идет тогда и только тогда когда нет ветра |
Задание 2.
Построить таблицы истинности для формул:
| I вариант | II вариант | III вариант |
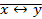 Úx Úx
| 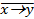 &x &x
| (x&y)® 
|
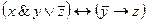
| 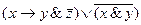
| 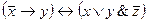
|
| IV вариант | V вариант | VI вариант |
( Úy)↔x Úy)↔x
| x®(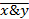 ) )
| x↔( ) )
|

| 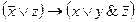
| 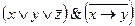
|
Задание 3.
С помощью равносильных преобразований упростить формулы логики:
| I вариант | II вариант | III вариант |
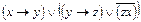
| x®(( )&(x& )&(x& 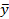 )) ))
| 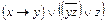
|
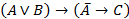
| 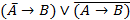
| 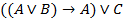
|
| IV вариант | V вариант | VI вариант |
((xy)®x) ®(xÚ 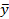 ) )
| (xy)® 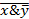
| x®( Ú Ú 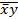 ) )
|
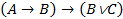
| 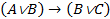
|
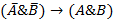
|
Задание 4.
Установить, равносильны ли следующие формулы двумя способами:
а) с помощью таблицы истинности
б) с помощью равносильных преобразований
| I вариант | II вариант |
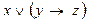 и и 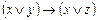
| 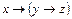 и и 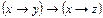
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем разница между простыми и составными высказываниями?
2. Как определяется количество строк в таблице истинности?
3. Какими способами можно определить равносильность формул логики?
Литература
1. В.И. Игошин Математическая логика и теория алгоритмов: учеб. пособие. – М.: Издательский центр «Академия», 2008.
2. В. И. Игошин Задачи и упражнения по математической логике и теории алгоритмов: учеб. пособие для студ. высш. учеб. заведений. - М.: Издательский центр «Академия», 2007
|
|
|
3. М.С.Спирина Дискретная математика: Учеб. для студ. сред. проф. образования. - М.: Издательский центр «Академия»,2004.
Практическая работа № 2
ПОСТРОЕНИЕ ДИЗЪЮНКТИВНОЙ И КОНЪЮНКТИВНОЙ НОРМАЛЬНЫХ ФОРМ
(ДНФ И КНФ). РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ.
ЦЕЛЬ РАБОТЫ: научиться определять ДНФ и КНФ, решать логические задачи средствами алгебры логики.
Для выполнения работы необходимо знать основные формулы алгебры высказываний, методы минимизации алгебраических преобразований; необходимо уметь формулировать задачи логического характера и применять методы математической логики для их решения.
Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.2.Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности; ПК 1.4. Участвовать в экспериментальном тестировании информационной системы на этапе опытной эксплуатации, фиксировать выявленные ошибки кодирования в разрабатываемых модулях информационной системы.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
С помощью равносильных преобразований формулу логики можно привести к дизъюнктивной или конъюнктивной нормальной форме (ДНФ и КНФ).
Дизъюнктивной нормальной формой называется дизъюнкция простых конъюнкций.
Пример 1. Привести к ДНФ формулу (X→Y)&(Y→Z).
Решение
Избавляемся от импликации в скобках;
2. раскрываем скобки, пользуясь законом дистрибутивности;
3. упрощаем выражение, пользуясь законом непротиворечия (Y  = 0) и законом константыдля нуля (XÚ0=X).
= 0) и законом константыдля нуля (XÚ0=X).
(X→Y)&(Y→Z) = ( ÚY)&(
ÚY)&( ÚZ) =
ÚZ) = 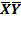 Ú
Ú  ZÚY
ZÚY  ÚYZ =
ÚYZ = 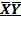 Ú
Ú  Z Ú YZ
Z Ú YZ
Ответ: (X→Y)&(Y→Z) = 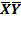 Ú
Ú  ZÚYZ.
ZÚYZ.
|
|
|
Конъюнктивной нормальной формой называется конъюнкция простых дизъюнкций.
Пример 2. Привести к КНФ формулу (Х®Y)(( ®Z)®
®Z)® 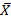 )
)
Решение
|
|
|


