 |
Краткая теория и методические рекомендации
|
|
|
|
Нормальная форма называется минимальной, если она включает минимальное число символов по сравнению со всеми другими эквивалентными ей нормальными формами.
Минимальная нормальная форма получается из СДНФ(СКНФ) удалением некоторых элементарных конъюнкций (дизъюнкций). Тупиковой нормальной формой называется ДНФ (КНФ),из которой нельзя удалить ни одной элементарной конъюнкции (дизъюнкции) так, чтобы сохранить булеву функцию неизменной
Пример 1. Пусть булева функция задана таблицей истинности.
а)составить СДНФ для данной функции; б) минимизировать СДНФ; в) построить логическую схему, реализующуюданную функцию.
| x | y | z | F(x,y,z) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Решение.
а) Найдем элементарные конъюнкции и составим СДНФ:
F(x,y,z) =  yzÚxy
yzÚxy  Úxyz
Úxyz
б) Минимизируем СДНФ с помощью равносильных преобразований:
F(x,y,z) =  yzÚxy
yzÚxy  Úxyz =(
Úxyz =( yzÚxyz)Úxy
yzÚxyz)Úxy  = yz(
= yz( Úx)Úxy
Úx)Úxy  = yzÚxy
= yzÚxy  = y(zÚx
= y(zÚx  ) = y(zÚx)(zÚ
) = y(zÚx)(zÚ  ) = y(zÚx)
) = y(zÚx)
в) Данную функцию реализует следующая логическая схема:
 |
Одним из наиболее удобных способов минимизации булевых функций является графический метод карт Карно. Карты Карно – это таблицы, состоящие из 2nклеток (n – количество переменных). В каждой клетке находится двоичное значение (0 или 1) булевой функции из таблицы истинности или из СДНФ.
При n = 3 карты Карно имеют вид таблицы с 23 = 8 клетками:
 00 00
|  10 10
|  11 11
| 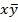 01 01
| |
| z 1 | ||||
 0 0
|
При n = 4 карты Карно имеют вид таблицы с 24 = 16 клетками.

|  d d
| zd | z 
| |

| ||||

| ||||
| хy | ||||
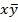
|
Пример 2. Дана функция F(x,y,z) =  y
y  Ú
Ú  yzÚxy
yzÚxy  Úxyz. Построить минимальную нормальную форму данной функции.
Úxyz. Построить минимальную нормальную форму данной функции.
|
|
|
Решение
1 способ: с помощью равносильных преобразований
F(x,y,z) =  y
y  Ú
Ú  yzÚxy
yzÚxy  Úxyz = (
Úxyz = ( y
y  Ú
Ú  yz)Ú(xy
yz)Ú(xy  Úxyz) =
Úxyz) =  y(
y( Úz) Úxy(
Úz) Úxy( Úz) =
Úz) =  yÚxy = y(
yÚxy = y( Úx) = y
Úx) = y
2 способ: с помощью карт Карно
1. Функция задана в виде СДНФ. Нанесем единицы на карту Карно (единицы соответствуют слагаемымв СДНФ):
 00 00
|   10 10
|   11 11
| 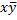 01 01
| |
| z 1 | 0 | 1 | 1 | 0 |
 0 0
| 0 | 1 | 1 | 0 |
2. Обведем единицы попарно двумя контурами.
3. В первом контуре не меняются переменные  , во втором – переменные
, во втором – переменные  .
.
4. Объединим получившиеся конъюнкции дизъюнкцией: F (x, y, z) =  Ú xy = y.
Ú xy = y.
В этой задаче можно рассмотреть весь квадрат из четырех единиц:
 00 00
|   10 10
|  11 11
| 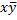 01 01
| |
| z 1 | 0 | 1 | 1 | 0 |
 0 0
| 0 | 1 | 1 | 0 |
В этом квадрате для всех единиц неизменной остается только переменная y, следовательно, F(x, y, z) = y.
Ответ: минимальная нормальная форма: F(x, y, z) = y.
Пример 3. Построить минимальную форму для булевой функции, заданнойтаблично.
| x | y | z | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Решение
1. Нанесем на карту Карно единицы в соответствии со значениями последнего столбца таблицы:
 00 00
|  10 10
|   11 11
| 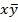 01 01
| |
| z 1 | 
| 1 | ||
 0 0
| 1 | 1 | 1 | 1 |
2. Обведем единицы в два контура.
3. В первом контуре, состоящем из четырех единиц не меняется переменная z, во втором – переменные  .
.
4. Объединим получившиеся результаты дизъюнкцией: F (x, y, z) =  Ú xy.
Ú xy.
Ответ: F(x,y,z) =  Úxy.
Úxy.
Кроме рассмотренных методов минимизации существуют также метод Куайна, метод диаграмм Вейча. Минимальную нормальную форму удобно использовать при построении логических схем.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ФОРМА ОТЧЕТНОСТИ
Задание 1. Привести СДНФк минимальной двумя способами: а) с помощью равносильных преобразований; б) с помощью карт Карно.
| I вариант | II вариант |
F(x,y,z) =  Ú Ú  Úx Úx 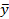 zÚxyz zÚxyz
| F(x,y,z) =  Ú Ú  Úx Úx 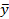 zÚxy zÚxy 
|
| III вариант | IV вариант |
F(x,y,z) =  Ú Ú  Úx Úx 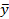 zÚxy zÚxy 
| F(x,y,z) =  Ú Ú  Ú Ú  zÚx zÚx 
|
Задание 2.
|
|
|
Для данной булевой функции а)составить СДНФ; б) минимизировать СДНФ с помощью равносильных преобразований и карт Карно; в) построить логическую схему, реализующую функцию.
| I вариант | II вариант | III вариант | IV вариант |
| F(x,y,z) = (11001000) | F(x,y,z) = (01010100) | F(x,y,z) = (11000100) | F(x,y,z) = (00110010) |
Задание 3. Постройте минимальную форму для функции, выраженной картой Карно.
I вариант

|  d d
| zd | z 
| |

| 1 | 1 | ||

| 1 | 1 | 1 | |
| 1хy | ||||
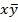
| 1 | 1 | 1 |
II вариант

|  d d
| zd | z 
| |

| 1 | 1 | ||

| 1 | 1 | 1 | |
| 1хy | 1 | |||
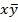
| 1 | 1 |
III вариант

|  d d
| zd | z 
| |

| 1 | 1 | 1 | |

| 1 | 1 | ||
| 1хy | ||||
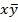
| 1 | 1 | 1 |
IV вариант

|  d d
| zd | z 
| |

| 1 | 1 | 1 | |

| 1 | 1 | ||
| 1хy | 1 | |||
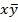
| 1 | 1 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие еще существуют методы минимизации булевых функций?
2. Почему при построении логических схем удобнее использовать минимальную форму булевой функции?
Практическая работа № 5
|
|
|


