 |
Краткая теория и методические указания
|
|
|
|
Нормальная форма называется совершенной, если в каждой ее элементарной дизъюнкции (конъюнкции) представлены все переменные, входящие в данную функцию (либо сами, либо с отрицанием).
Пример 1. Найти СДНФ для булевой функции: F(x,y,z) = (x↔y)Ú(y↔z) аналитическим способом и с помощью таблицы истинности.
Решение.
а) С помощью законов логики заменим эквиваленцию дизъюнкцией и отрицанием, приведембулеву функцию к ДНФ.
F(x,y,z) = (x↔y)Ú(y↔z) = (xyÚ  ) Ú(yzÚ
) Ú(yzÚ  ) = xyÚ
) = xyÚ  ÚyzÚ
ÚyzÚ  .
.
Т.к. в каждом слагаемом не хватает по одной переменной, умножим каждое слагаемое на 1, и затем представим 1 в виде: 1 = аÚ 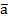 (вместо а необходимо записать недостающую переменную)
(вместо а необходимо записать недостающую переменную)
F(x,y,z) =xy1Ú  1Úyz1Ú
1Úyz1Ú  1=xy(zÚ
1=xy(zÚ  )Ú
)Ú  (zÚ
(zÚ  )Úyz(xÚ
)Úyz(xÚ  )Ú
)Ú  (xÚ
(xÚ  )= xyz Úxy
)= xyz Úxy  Ú
Ú  zÚ
zÚ 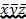 Ú yzx Úyz
Ú yzx Úyz  Ú
Ú
Ú  xÚ
xÚ  = xyz Ú xy
= xyz Ú xy 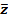 Ú
Ú 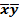 z Ú yz
z Ú yz  Ú
Ú 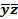 x Ú
x Ú 
б) Построим таблицу истинности для функции F(x,y,z) = (x↔y)Ú(y↔z).
| x | y | z | x↔y | y↔z | (x↔y)Ú(y↔z) |
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
В последнем столбце выделим наборы, для которых значение функции истинно и для каждого набора построим элементарные конъюнкции, причем каждой переменной xk=1 будет соответствовать xk, а каждой xk=0 будет соответствовать  k. Далее составляем дизъюнкции построенных элементарных конъюнкций.
k. Далее составляем дизъюнкции построенных элементарных конъюнкций.
F(x, y, z) = xyz Ú 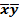 z Ú
z Ú  yz Ú x
yz Ú x 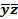 Ú xy
Ú xy 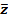 Ú
Ú 
Ответ: СДНФF(x,y,z) = xyzÚxy  Ú
Ú  zÚyz
zÚyz  Ú
Ú  xÚ
xÚ 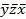
Пример 2. Найти СКНФ для булевой функции: F(x,y,z) = (xÚy)(z®x) аналитическим способом и с помощью таблицы истинности.
|
|
|
Решение.
а) С помощью законов логики заменим импликацию дизъюнкцией и отрицанием и приведембулеву функцию к КНФ.
F(x,y,z) = (xÚy)(z®x) = (xÚy)( Úx).
Úx).
Т.к. в каждом слагаемом не хватает по одной переменной, прибавим к каждому слагаемое 0, и затем представим 0 в виде: 0 = а 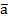 (вместо а необходимо записать недостающую переменную)
(вместо а необходимо записать недостающую переменную)
F(x,y,z) = (xÚyÚ0)( ÚxÚ0)=(xÚyÚz
ÚxÚ0)=(xÚyÚz  )(
)( ÚxÚy
ÚxÚy 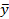 )=(xÚyÚz) (x Ú y Ú
)=(xÚyÚz) (x Ú y Ú 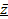 )(
)( 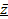 Ú x Ú y) (
Ú x Ú y) ( ÚxÚ
ÚxÚ 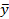 ) = (xÚyÚz) (
) = (xÚyÚz) ( ÚxÚy) (
ÚxÚy) ( ÚxÚ
ÚxÚ 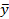 ).
).
б) Построим таблицу истинности для функции F(x,y,z) = (xÚy)(z®x).
| x | y | z | xÚy | z®x | (xÚy)(z®x) |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
В последнем столбце выделим наборы, для которых значение функции ложно и для каждого набора построим элементарные дизъюнкции, причем каждой переменной xk=1 будет соответствовать  k, а каждой xk=0 будет соответствовать xk. Далее составляем конъюкнции построенных элементарных дизъюнкций.
k, а каждой xk=0 будет соответствовать xk. Далее составляем конъюкнции построенных элементарных дизъюнкций.
F(x, y, z) = (x Ú y Ú z) ( 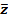 Ú x Ú y) (
Ú x Ú y) ( 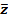 Ú x Ú
Ú x Ú 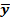 )
)
Ответ: СКНФ:F(x,y,z) = (xÚyÚz) ( ÚxÚy) (
ÚxÚy) ( ÚxÚ
ÚxÚ 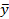 )
)
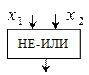
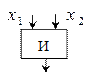
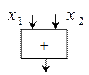
Устройства, реализующие элементарные булевые функции, называются логическими элементами. Логические элементы изображаются в виде прямоугольников, внутри которых помещаются условные названия или символы соответствующих функций:
| Функция |  Графическое изображение Графическое изображение
| Функция | 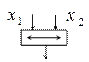 Графическое изображение Графическое изображение
|
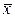
| 
| 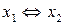
| 
|
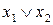
| 
| 
| 
|
| 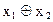
|
Из данных логических элементов путем соединения входа одного из них с выходом другого можно строить сложные логические схемы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ФОРМА ОТЧЕТНОСТИ
Задание 1.
Найти СДНФ для булевой функции а) аналитическим способом; б) с помощью таблицы истинности.
|
|
|
| I вариант | II вариант | III вариант | IV вариант |
F(x,y,z) = ( ®yz)Ú(y↔z) ®yz)Ú(y↔z)
| F(x,y,z) = ( ®z)Ú ®z)Ú 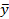 z z
| F(x,y,z) = ( ↔y)Ú(x®yz) ↔y)Ú(x®yz)
| F(x,y,z) = (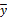 ® ®  )Úxz )Úxz
|
Задание 2.
Найти СКНФ для булевой функции а) аналитическим способом; б) с помощью таблицы истинности.
| I вариант | II вариант | III вариант | IV вариант |
F(x,y,z) = ( ®z)( ®z)(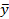 Úx) Úx)
| F(x,y,z) = ( Úz)(y®z) Úz)(y®z)
| F(x,y,z) = (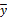 ® ® 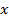 )(xÚz) )(xÚz)
| F(x,y,z) = (xÚy)(x®z) |
Задание 3. Для данной булевой функции построить логическую схему
| I вариант | II вариант | III вариант | IV вариант |
F(x,y,z) = (xÚy)( Åz) Åz)
| F(x,y,z) = ( &y)Ú &y)Ú  êz) êz)
| F(x,y,z) =(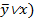 ( ( Åz) Åz)
| F(x,y,z) = (x& 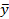 )Ú )Ú 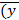 êz) êz)
|
Задание 4.
По заданной логической схеме построить булеву функцию и составить ее таблицу истинности:
Iвариант

II вариант

 III вариант
III вариант
IV вариант

КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие законы логики применяются для ввода недостающих переменных при представлении булевой функции в виде СДНФ и СКНФ?
2. Приведите примеры логических схем, используемых в ЭВМ.
Литература
1. В.И. Игошин Математическая логика и теория алгоритмов: учеб. пособие. – М.: Издательский центр «Академия», 2008.
2. В. И. Игошин Задачи и упражнения по математической логике и теории алгоритмов: учеб. пособие для студ. высш. учеб. заведений. - М.: Издательский центр «Академия», 2007
3. Спирина М.С. Дискретная математика: Учеб. для студ. сред. проф. образования. - М.: "Академия", 2004
Практическая работа № 4
|
|
|


