 |
§ 3. Метод двухальтернативного вынужденного выбора (2АВВ)
|
|
|
|
В методе 2АВВ предъявления всегда осуществляются парами, причем предъявления в одной паре либо следуют друг за другом во времени, либо осуществляются одновременно, но ясно разделены пространственно. Одна пара всегда состоит из < S> и < N>, и это испытуемому известно, но какое именно из предъявлений (первое или второе, правое или левое и т. п. ) содержит сигнал, а какое является пустым, должен определить испытуемый. Например, предъявляется пара линий, одна из которых наклонена, а другая вертикальна. Линии располагаются слева и справа от фиксационной точки и после каждого предъявления испытуемый должен решить, какая линия (слева или справа) имела наклон. Другой пример. Испытуемый слышит постоянный белый шум. Во время прослушивания дважды (скажем, с интервалом в полсекунды) загорается и гаснет (в течении 50 мс) индикатор начала и конца предъявления. В одном из двух предъявлений к шуму добавляется слабый тон частотой 1000 Гц, и задача испытуемого состоит в том, чтобы указать, в первом или во втором предъявлении присутствовала тональная добавка.
Чтобы различать варианты организации пары стимулов, условимся один из элементов пары называть " первым" и записывать на первом месте, а другой — " вторым" и записывать на втором месте. Таким образом пара может иметь либо форму < S, N>, либо форму < N, S>. Допустим, если в нашем первом примере наклонная линия находится слева, мы имеем < Н, В>, а если справа — < В, Н>, где В означает " вертикальна", Н — " наклонна". Соответственно, если испытуемый считает, что наклонная линия находится слева, то его ответ может быть записан как " < Н, В> ". В общем случае матрица стимулов-ответов представима в форме:
|
|
|
Во всех остальных отношениях 2АВВ ничем не отличается от метода " Да-Нет". Если условиться идентифицировать пару по ее первому элементу, то можно даже не менять обозначений. Например,
P(S) = P(< S, N> ), P(N) = P(< N, S> ) == 1 - P(S).
Правильный ответ 1 можно условно считать попаданием и обозначать его условную вероятность через р(Н) = р(" Да", " Нет" /< S, N> ); ошибку 2 можно условно считать ложной тревогой и использовать обозначение p(FA) = p(" Да", " Нет" /< N, S> ) и т. д. Аналогично методу " Да-Нет" вводятся платежные матрицы, обратная связь, предварительная информация. Укажем, однако, на одно существенное отличие. Если в методе " Да-Нет" P(S) и платежная матрица таковы, что мы допускаем, что субъективные цены обеих ошибок (FA и О) одинаковы, то вовсе не необходимо, чтобы условные вероятности этих ошибок были равны. Или, что то же самое, нет оснований, вообще говоря, ожидать, что р(Н) = p(CR). В методе 2АВВ, однако, пары < S, N> и < N, S> симметричны и при сделанных предположениях условные вероятности правильных ответов 1 и 2 должны быть равны. Это интуитивное соображение подкрепляется теоретической моделью, к изложению которой мы переходим. Но прежде введем новое обозначение. Условимся через р(С) (от английского correct — правильный) обозначать суммарную вероятность правильного ответа:
Результаты 2АВВ называются несмещенными, если р(Н) = p(CR) или, что то же самое, p(H) + p(FA) = l.
Теоретическая модель 2АВВ является простым распространением модели, изложенной в предыдущем разделе. Мы сразу предположим, что все сделанные там допущения и упрощающие предположения сохраняют свою силу по отношению к < S> и < N> по отдельности, а когда < S> и < М> объединяются в пару, их сенсорные репрезентации независимы друг от друга, причем испытуемый никогда не путает, какому (" первому" или " второму" ) члену пары соответствует данный образ. Каждый образ оценивается по интенсивности некоторого выбранного качества, так что образ пары оценивается по паре интенсивности сенсорного качества < Х1, Х2>, записанных в той же последовательности, что и стимулы. Если предъявляется < S, N>, то XI имеет распределение f(X/S), X2 — распределение f(X/N). Если предъявляется < N, S>, то наоборот XI распределяется по f(X/N), a X2 — по f(X/S). Имея < Х1, Х2>, испытуемый должен решить, первая или вторая интенсивность соответствует < S>. Естественным правилом решения здесь является следующее: берется разность XI-X2 и сравнивается с критическим значением С*. Если X1 - X2 > С*, то дается ответ " Да, Нет", если же X1 - X2 < С* то " Нет, Да". Как видим, С* играет здесь ту же роль, что и критерий С в методе " Да-Нет". Заметим, что разность берется всегда в одном и том же направлении, скажем от " первой" интенсивности ко " второй", Х1-Х2, независимо от того, было ли предъявлено < S, N> или < N, S>. Начнем с рассмотрения случая предъявления < S, N>. Поскольку X1 и X2 суть случайные величины, то их разность тоже является случайной величиной, распределение которой мы обозначим через f(Δ x/< S, N> ). f(Δ x/< S, N> ) есть плотность вероятности того, что X1 - X2 = Δ х при предъявлении < S, N>. Эта функция однозначно определяется, если известны два распределения f(X/S) и f(X/N). Пусть теперь предъявлена пара < N, S>. Очевидно, что в этом случае разность X2 – X1 распределена точно так же, как разность X1 - X2 в первом случае, т. е. плотность вероятности события X2 – X1 = Δ x/< N, S> равна плотности вероятности события X1 - X2 = Δ х/< S, N>; но ведь событие X1 - X2 = Δ х/< S, N> равносильно событию X2 – X1 = Δ x/< N, S>. Мы получаем важное соотношение:
|
|
|
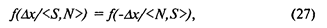
где разность всегда берется от " первой" интенсивности ко " второй", Х1-Х2. Соотношение (27) означает, что функции распределения f(Δ x/< S, N> ) и f(Δ x/< N, S> ) являются зеркально симметричными. В этом существенное отличие теоретической схемы для 2АВВ от теоретической схемы для метода " Да-Нет": f(X/S) и f(X/N) могут быть сколь угодно непохожими друг на друга, но f(Δ x/< S, N> ) и f(Δ x/< N, S> ) являются зеркальными копиями. Введем в теоретическое представление критерий С*. На рис. 12 заштрихованные области равны по площади вероятностям p(CR) и р(Н). Легко видеть, что несмещенный 2АВВ, при котором p(CR) = р(Н), будет иметь место только в случае С* = 0. При отрицательных С* испытуемый будет более часто правильно указывать сигнал, если сигнальное предъявление было " первым", чем если оно было " вторым" (при этом говорят, что наблюдатель имеет предрасположение к " первому" стимулу). При С*> 0 испытуемый имеет предрасположение ко " второму" стимулу: p(CR) > р(Н). Двигая С* справа налево и фиксируя различные пары р(Н), p(FA) (p(FA) = 1 - p(CR)), мы можем построить кривую РХ для 2АВВ (рис. 13).
|
|
|
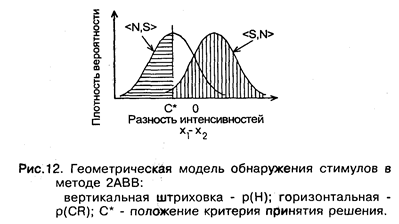
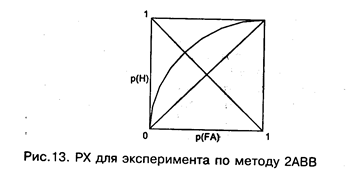
В силу зеркальной симметричности распределений кривая РХ для 2АВВ всегда симметрична относительно побочной диагонали. Это следствие в принципе позволяет экспериментально проверить валидность схемы с оценкой разностей X1 - Х2, но, к сожалению, строгое статистическое доказательство симметричности РХ провести довольно сложно. В эксперименте различные точки РХ можно получить, задавая асимметричные платежные матрицы (например, штрафуя за пропуск " первого" сигнала значительно больше, чем за пропуск " второго" ), подавая одну комбинацию (например, < S, N> ) чаще, чем другую и т. д. — совершенно аналогично методу " Да-Нет".
До сих пор мы не использовали предположения о возможности монотонной трансформации Х в Z, при которой f(X/S) и f(X/N) переходят в нормальные распределения f(Z/N) и f(Z/S). Если теперь это предположение принять и использовать разности Zl - Z2, то можно показать следующее: если f(Z/N) имеет центр равным 0 и дисперисию равной 1, a f(Z/S) - центр в точке а и дисперсию равной σ, то f(Δ Z/< S, N> ) и f(Δ Z/< N, S> ) являются тоже нормальными распределениями с одной и той же дисперсией, равной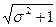 
и с центрами, соответственно, в точках а и -а (см. рис. 14).
Рассмотрим, каковы соотношения между вероятностями р(Н) и p(FA) при произвольном значении С*. Для этого сдвинем левое распределение вместе с критерием До совмещения его центра с нулем и сожмем ось Z ровно в 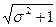раз. Распределение после этого станет табличным, а критерий займет позицию 
. Отсюда:
|
|
|
Вернемся теперь к исходной картинке и, сдвинув правое распределение вместе с критерием влево на а и, сжав z-ось в 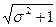раз, получим:
Итак, в двойных нормальных координатах РХ для 2АВВ описывается прямой линией с наклоном 45 градусов (заметьте, при любой величине σ ). Отсюда следует способ экспериментальной проверки предположения о нормальности f(z/S) и f(z/N) в методе 2АВВ: по z-преобразованным точкам РХ строится прямая наилучшего приближения, проверяется удовлетворительность приближения и незначимость отличия наклона от 45 градусов. Если дополнительно предположить, что σ = 1, т. е. f(z/S) и f(z/N) имеют одинаковые дисперсии, то свободный член в формуле (32) станет равен 
(или, применяя стандартное обозначение, d'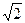 
). В этом случае для разности z[p(H)] - z[p(FA)] в 2АВВ тоже иногда используют обозначение d' и пишут:
Часто это соотношение (не очень корректно) читается так: чувствительность в 2АВВ в 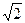выше, чем в " Да-Нет". Этот вывод вряд ли покажется неожиданным для психолога, поскольку почти очевидно, что в условиях, где у испытуемого имеется возможность сравнения, результаты будут выше, чем в тех условиях, где такая возможность отсутствует (метод " Да-Нет" ).
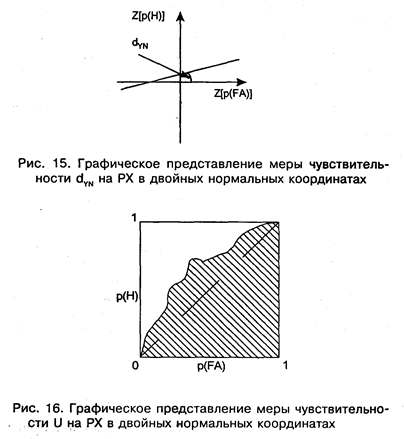
В заключение мы остановимся на одном удивительном соотношении между 2АВВ и методом " Да-Нет". Мы знаем, что чувствительность (отличимость сигнального стимула от пустого) может быть измерена числом d', если на распределении f(X/S) и f(X/N) наложено весьма жестко требование о существовании монотонной трансформации X®Z, переводящей эти распределения в два нормальных с равными дисперсиями. Если это требование не выполняется, но f(X/S) и f(X/N) могут быть переведены путем монотонной трансформации в два нормальных распределения с разными дисперсиями, то в методе " Да-Нет" чувствительность характеризуется уже парой чисел (a, s), что весьма неудобно, поскольку к парам чисел неприложимы оценки " больше-меньше", " возрастает-убывает" и т. д. Разумеется, в этом случае можно предложить какую-либо другую скалярную, (т. е. выразимую одним действительным числом) меру чувствительности (на рис. 15 показана одна такая мера, называемая dyn), которая с формальной точки зрения будет являться скалярной функцией от а и s (например, dYN = 
).
Или можно обратиться к 2АВВ, взяв за меру чувствительности свободный член уравнения (32). Однако часто возникает вопрос, что делать в том случае, когда проверка отвергает предположение о нормальности? Существует ли какая-либо простая скалярная мера чувствительности, применимая при любых f(X/S) и f(X/N)? Такая мера действительно существует: площадь под кривой РХ. Интуитивно эта мера представляется весьма удачной. Она универсальна (применима к любой РХ) и всегда позволяет сказать, в каком сигнальном стимуле, S1 или S2, сигнал более обнаруживаем (в сопоставлении с одним и тем же N). Но у этой меры (обозначим ее U, см. рис. 16) есть существенный недостаток — для ее вычисления необходимо знать достаточно много точек РХ.
|
|
|
Допустим, однако, что для некоторой пары < N> и < S> было проведено подробное исследование и вычислена мера U. Пусть теперь мы используем теже < S> и< N> в методе 2АВВ. Мы провели всего один эксперимент и получили (с точностью до статистических вариаций) следующий результат:
Результаты показывают, что выбор является несмещенным: р(Н) = p(CR). Мы знаем, что в этом случае общая вероятность правильного ответа Р(С) (см. формулу (26)) равна р. Удивительное соотношение между " Да-Нет" и 2АВВ, о котором идет речь, состоит в том, что если изложенная модель обнаружения верна, то должно быть U = р. Другими словами: в несмещенном случае P(C)2ABB = U" Да-Нет" . Таким образом, в качестве хорошей и простой (пожалуй, самой простой) меры чувствительности в 2АВВ может использоваться процент правильных ответов Р(С).
|
|
|
