 |
Вероятности исходов эксперимента с симметричной платежной матрицей и P(S)=0.5
|
|
|
|
Вероятности исходов эксперимента с симметричной платежной матрицей и P(S)=0. 5

Это положение критерия оптимально в том смысле, что суммарный выигрыш испытуемого в этом случае будет максимален.
Пусть теперь в следующем эксперименте платежная матрица осталась симметричной, a P(S) = 0. 9.
Таблица 3
Вероятности исходов эксперимента с симметричной платежной матрицей и P(S)=0. 9

Теперь (рис. 6б), чтобы сохранить тот же выигрыш, наблюдателю необходимо сдвинуть критерий так, чтобы р(Н) резко возросло, даже за счет возрастания p(FA) — теперь важнее не пропустить сигнал, чем не дать ложную тревогу! Следовательно, критерий С сдвинется влево. В данном случае говорят, что наблюдатель использует либеральный критерий.
Пусть в третьем эксперименте при симметричной платежной матрице P(S) установили равной 0. 1.
Таблица 4
Вероятности исходов эксперимента с симметричной платежной матрицей и P(S)=0. 1

В этой ситуации (рис. 6в) критерий должен быть сдвинут вправо, и в этом случае говорят об использовании строгого критерия. Аналогичные изменения положения критерия принятия решения можно рассмотреть и при изменениях платежной матрицы при постоянной величине P(S).
Для каждой пары f (X/S) и f (X/N), если заданы V, W и P(S), может быть рассчитано оптимальное положение С — то, при котором выигрыш максимален. В соответствии с данной логикой можно исследовать вопрос, насколько реальное положение критерия, выбираемое испытуемым, близко к оптимальному. Но, разумеется, это можно сделать лишь в том случае, если мы можем восстановить по результатам экспериментов теоретическую схему, т. е. построить функции распределения f (X/S) и f (X/N) и найти критерий С.
|
|
|
Итак, перед нами стоит задача восстановления теоретической схемы по экспериментальным данным. Прежде всего, разберемся в том, что представляют собой экспериментальные данные. Пусть выбраны стимулы < S> и < N> и проведен эксперимент по методу " Да-Нет". Результатом эксперимента является пара вероятностей р(Н), p(FA). Далее какие-то параметры эксперимента меняются (из-менятеся P(S) и/или платежная матрица, или снимается обратная связь и заменяется на предварительную информацию или что-то еще), и эксперимент повторяется с теми же < S> и < N>. Получаем, вообще говоря, другую пару р(Н), p(FA). Повторяя эксперимент несколько раз, мы будем иметь в результате несколько пар р(Н), p(FA), т. е. несколько точек РХ. Разумеется, и это очень важно, мы можем считать все эти пары р(Н) и р(РА) точками одной РХ лишь постольку, поскольку предполагается, что изменения экспериментальных параметров могут привести только к изменению положения критерия С, но не к изменению схемы соответствия, в более широком смысле слова включающем возможное привлечение новых сенсорных качеств, замену одного качества на другое и в результате, если это новое качество одномерно, — получению новой пары распределений f(X/S) и f (X/N). Таким образом, проблема формулируется так: по нескольким точкам РХ нужно восстановить f (X/S), f (X/N) и С. Однако, мы уже говорили, что в таком виде проблема не решается, так как даже если бы была известна вся РХ (т. е. все точки, а не несколько, чего никогда, естественно, не бывает), распределения f (X/S) и f (X/N) не восстановимы однозначно. Поэтому в модели, которую мы излагаем (обычно называемой, хотя и не совсем точно, теорией обнаружения сигналов, ТОС) принимается еще одно упрощающее предположение (впрочем, в отличие от первого, оно допускает прямую экспериментальную проверку, о чем речь пойдет ниже): существует такая монотонная трансформация оси интенсивности, в результате которой оба распределения становятся нормальными. Для краткости трансформированную ось мы будем обозначать просто через z и говорить о z-значениях. Под монотонной трансформацией понимается система всевозможных растяжений и сжатий различных областей оси Х так, что если точка q лежит левее r, то после трансформации это отношение сохраняется. Примером такой трансформации является логарифмирование, растягивающее положительную полуось действительных чисел на всю действительную ось. Итак, мы имеем два нормальных распределения, причем всегда можно считать, что на оси выбрана такая позиция нуля и такой масштаб, что f (Z/N) имеет центр в нуле и стандартное отклонение, равное 1. Для восстановления теоретической картины, таким образом, необходимо определить положение центра и стандартное отклонение распределения f (Z/S).
|
|
|
Если допустить, что σ s, n = 1, т. е. дисперсии обоих распределений равны, а центр распределения f (Z/S) сдвинут вправо от центра распределения f(Z/N) на величину а, тогда
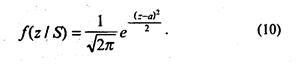

В этом случае вместо а обыкновенно пишут специальный символ d' и называют эту величину мерой чувствительности наблюдателя к сигналу. Чувствительность к сигналу характеризуется степенью отличия Z-величин, вызываемых < S>, от Z-величин, вызываемых < N>. Чем меньше величина d', тем больше перекрываются области Z-значений, соответствующих < S> и < N> (рис. 7).
Легко видеть, что при одном и том же положении критерия С, а следовательно, при одной и той же величине p(FA), величина р(Н) тем ближе к p(FA), чем меньше d'. Если d' = 0, то p(FA) = р(Н) при всех С и, следовательно, РХ в таком эксперименте совпадает с главной диагональю квадрата (рис. 8). Если d' > 0, РХ лежит выше диагонали и имеет гладкий и симметричный вид относительно побочной диагонали, идущей из (0, 1) в (1, 0). Чем больше d', тем более выпукла РХ влево-вверх и тем дальше она отстоит от главной диагонали. Как же практически вычислить d' и С по результатам эксперимента? Сколько точек РХ следует для этого иметь?

Оказывается, достаточно только одной точки, т. е. только одной пары p(FA), p(H). Действительно,
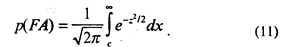
Это уравнение необходимо решить относительно С. Введем новый термин: нахождение С по Р в уравнении (12):
|
|
|

Сделать Z-преобразование можно по обычной таблице нормального распределения. Если есть таблица, показывающая для каждого С значение интеграла (12), то нужно попросту отыскать в таблице значение интеграла, наиболее близкое к Р, и посмотреть слева, какому С оно соответствует. Легко показать, что уравнение (11) в терминах Z-преобразования имеет решение:

Теперь допустим, что С найдено. Как, зная р(Н), найти величину d'? Рассмотрим теоретическую картинку, из которой удалено распределение, соответствующее N (оно уже не понадобится, см. рис. 9а). Сдвинем все распределение вдоль оси Z вместе с критерием С влево так, чтобы центр совместился с точкой 0. Критерий С при этом, очевидно, займет позицию (С - d'), а заштрихованная область не изменится и останется равной по площади р(Н) (см. рис. 9б). Но наше сдвинутое распределение имеет центр в нуле и единичную дисперсию.

Следовательно:

Допустим теперь, что проведен новый эксперимент с измененными параметрами, так что получена новая пара p(FA) и р(Н). Если наше предположение относительно f (Z/S) и f (Z/N) верно (т. е. они оба нормальны и имеют одну и ту же дисперсию), то, несмотря на изменение величины С прямо определяемой по формуле (14), величина d’, определяемая по формуле (17), должна оставаться постоянной. Мы приходим к важному заключению: если по оси абсцисс откладывать величины Z[p(FA)], а по оси ординат — z[p(H)], то точки РХ должны выстроиться в прямую линию, описываемую уравнением (17): z[p(H)] = z[p(FA)] + d', и наклоненную под 45° к оси абсцисс. График зависимости Z[p(H)] от Z[p(FA)] (см. рис. 10) называется РХ в двойных нормальных координатах. Из соотношения (17) вытекает способ экспериментальной проверки предположений, принятых о нормальности распределений и равенстве дисперсий. Пусть мы провели К экспериментов и получили К точек РХ (К ≥ 2).
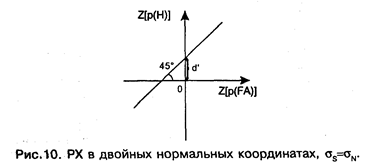
Построим РХ в двойных нормальных координатах: z[p(FA)] и z [p(H)j. Поскольку вероятности р(Н) и p(FA) оценивались по частотам (т. е. мы имеем лишь их приблизительные значения), то точки; соответствующие z-преобразованиям, будут отклоняться от теоретической прямой (с наклоном 45 градусов) даже в том случае, если проверяемые предположения верны. Следовательно, надо провести прямую наилучшего приближения и проверить с помощью стандартных статистических средств, значимо или не значимо ее наклон отличается от 45°. Если отличие не значимо, исходные предположения могут считаться верными, а величина свободного члена в формуле прямой дает нам статистическую оценку d'. Разумеется, всем этим выводам должна предшествовать проверка того, является ли расположение экспериментальных точек хорошим приближением к прямой линии, т. е. необходимо провести статистический тест на линейность.
|
|
|
Допустим теперь, что удалось показать, что z-преобразованная РХ не является прямой с наклоном в 45 градусов. Тогда мы можем обратиться к более общему варианту нашей теоретической схемы: допустить, что σ s распределения f(z/S) произвольна, но оба распределения нормальны. Очевидно, формула (14) сохраняет свою силу, так как С определяется только по p(FA). Изменения по отношению к случаю с σ s, n = 1 появляются лишь в том месте, где распределение f(z/S) вместе с критерием С сдвигается влево до совмещения центра с нулевой точкой. Теперь мы уже не можем написать формулы (15) и (16), так как сдвинутое распределение описывается формулой:  . Однако, если мы вдобавок к сдвигу сожмем ось Z ровно в σ раз, то распределение приобретет нужную нам табличную форму. При этом критерий С, который после сдвига занял позицию С - а (мы уже не напишем d' вместо а), займет позицию . Итак:
. Однако, если мы вдобавок к сдвигу сожмем ось Z ровно в σ раз, то распределение приобретет нужную нам табличную форму. При этом критерий С, который после сдвига занял позицию С - а (мы уже не напишем d' вместо а), займет позицию . Итак:
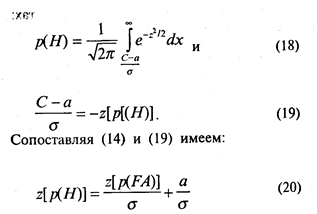
Итак, если оба распределения нормальны, то график РХ в двойных нормальных координатах должен быть прямой линией с наклоном 1/σ (см. рис. 11). Для проверки предположения о нормальности нужно оценить возможность описания экспериментальных точек линейной функцией или, (другими словами) " хорошесть" подгонки прямой линии к экспериментальным точкам.

На основании статистических оценок предположение о нормальности отвергается, если даже наилучшая (в смысле метода наименьших квадратов, например) прямая плохо подходит к данным.
Предположим, что распределения f(z/S) и f(z/N) имеют одинаковые дисперсии, то есть РХ в двойных нормальных координатах является прямой линией с наклоном 1. Положение каждой отдельной точки на РХ соответствует некоторому положению критерия С.
Можно показать, что при сделанных нами допущениях о нормальности распределений и равенстве дисперсий каждому положению С взаимно однозначно соответствует так называемое отношение правдоподобия (в точке С) — β, которое определяется как:
|
|
|

Здесь f(C/S) и f(C/N) представляют собой значения функций плотности вероятности f(X/S) и f(X/N), взятые в критической точке С. Отношение правдоподобия β характеризует то, во сколько раз правдоподобнее, что сенсорная репрезентация, равная по величине значению С, будет вызвана значащим стимулом, чем стимулом пустым.
По некоторым теоретическим соображениям положение критерия принято характеризовать именно этим значением β, а не самой величиной С.
Значения f(C/S) и f(C/N) легко найти, зная р(Н) и p(FA). Для этого необходимо воспользоваться таблицей плотности нормального распределения: найти значения плотностей, соответствующие Z[p(H)] и Z[p(FA)] (что мы уже умеем делать). Эти значения обозначаются через f[p(H)] и f[p(FA)]. Таким образом:

Оказывается, однако, что не обязательно искать f-преобразования для того, чтобы вычислить β. Вместо этого проще (и полезнее) вычислить lnβ прямо по z-преобразованным вероятностям. Дело в том, что в формулы, выражающие р(Н) и p(FA) через d' и β, последняя входит только в форме lnβ (попытайтесь сами вывести эти соотношения):
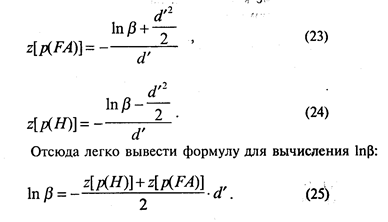
|
|
|


