 |
Исходы эксперимента по обнаружению сигнала
|
|
|
|

Попадание и ложная тревога будут в дальнейшем обозначаться через Н (от английского hit) и FA (от английского false alarm). Обозначения для пропусков и правильных отрицаний — О (omission) и CR (correct rejection). Пусть мы пересчитали количество сочетаний каждого типа: h (Н), n (FA), n (О), n (CR). Очевидно, что:
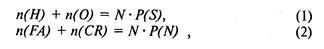
Зная эти качества и нормировав каждое из них по N (т. е., поделив на общее количество предъявленных проб), мы получим статистические оценки вероятностей появления исходов каждого типа:
Р(Н) = n(H)/N, Р(0) = n(0)/N, ... и т. д. (3)
Однако такие вероятности еще не говорят нам прямо о способности наблюдателя обнаруживать сигнал. Действительно, величина р(Н) зависит не только от того, как часто наблюдатель идентифицирует < S> как сигнал, но и от того, сколь часто предъявлялось в эксперименте < S>. Поэтому, чтобы охарактеризовать деятельность испытуемого в данном эксперименте, отделив ее от деятельности экспериментатора (решающего, в частности, сколько раз предъявить < S>, а сколько — < N> ), принято представлять результаты эксперимента в виде оценок условных вероятностей — вероятностей того, что испытуемый ответит правильно (неправильно) при условии, что был предъявлен данный стимул. Такие вероятности обозначаются так: Р (" Да" /S), Р (W/N), P (" Heт" /S), P (" Нет" / N). В частности, первая из этих вероятностей есть вероятность правильного ответа при условии, что было предъявлено < S>. Легко видеть, что:

Если вычислены две эти условные вероятности, вычисление двух остальных уже не требуется. Они не несут дополнительной информации, т. к.:

Итак, при данных (выбранных экспериментатором) величинах N и P(S) результаты эксперимента обычно представляют только двумя условными вероятностями: вероятностью попадания — р(Н) = Р(" Да" /S) и вероятностью ложной тревоги р(FА) = Р(" Да" /N).
|
|
|
Заметим, что при всех приведенных выше расчетах из общего числа N предъявлений обычно исключают несколько первых (порядка 40—50), предполагая, что в этих первых пробах испытуемый постоянно меняет схему соответствия, " подстраивая" ее к информации, полученной от экспериментатора и в ходе эксперимента. Когда схема соответствия устанавливается стабильно, говорят, что решение задачи вышло на асимптотический уровень. Асимптотический уровень характеризуется тем, что если все число предъявлений (после исключения первых) произвольно разбито на несколько групп и по каждой из них в отдельности вычислено Р(Н) и P(FA), то все эти пары не будут статистически значимо отличаться друг от друга.
Полная характеристика эксперимента требует указания еще двух факторов: наличие/отсутствие предварительной информации и наличие/отсутствие обратной связи. Предварительная информация — это формальный признак, означающий сообщение испытуемому величины P(S). Например: " В 80% всех проб будет предъявляться пустой стимул" (т. е. P(S) = 0, 2) или — " Сигнальное предъявление будет встречаться в 3 раза чаще пустого" (P(S)/P(N) = 3, т. е. P(S) = 0, 75). Сама инструкция, разъяснение испытуемому формы предъявления, характера сигнала и т. п. — все это не входит в термин " предварительная информация". Заметим, что предварительная информация, если она вводится, может быть и ложной, т. е. испытуемому может сообщаться не та величина P(S), которая есть на самом деле. Эта специальная модификация " Да-Нет" -эксперимента, которая здесь рассматриваться не будет. Термин обратная связь включает информацию об истинности/ложности ответов испытуемого, сообщаемую ему после каждого предъявления, или сообщение о частоте правильных ответов, даваемое после некоторой группы (скажем, через каждые 50) предъявлений. В специальных модификациях метода такая обратная связь также не всегда должна быть истинной. Иногда, например, используют такой вариант, когда после каждой пробы (предъявления) испытуемому с вероятностью P(k) сообщают важную информацию о правильности или ложности его ответа, а с вероятностью 1 - P(k) его " обманывают" (в этом варианте P(k) — формальная мера правдивости обратной связи).
|
|
|
Цель введения обратной связи и предварительной информации — попытка контроля схемы соответствия между свойствами ощущений и принимаемыми решениями, которую устанавливает испытуемый (правила принятия решения). Очевидно, однако, что если испытуемый не очень заинтересован в том, чтобы почаще отвечать правильно, то такой контроль может оказаться неэффективным*. Кроме того, испытуемый может, устанавливая правило принятия решения, руководствоваться неизвестными экспериментатору субъективными " весами" различных типов ошибок. Например, он может стараться минимизировать число пропусков и не очень заботиться об уменьшении числа ложных тревог (т. е. " цена" пропуска выше " цены" ложной тревоги). Чтобы сделать контроль правила принятия решения более эффективным и дифференцированным, обратная связь может быть дополнена системой " выплат" и " штрафов", соответственно за верные и ложные ответы, организованной в денежной или какой-либо другой (например, просто игровой) форме. Это можно записать в форме следующей платежной матрицы:

где V и W — положительные числа. Такая форма представления особенно удобна, так как она позволяет ограничиться только двумя числами, V и W, для характеристики всей платежной матрицы. Матрица называется симметричной, если V = W. Для определения оптимального правила принятия решения, т. е. такого из имеющегося у наблюдателя набора возможностей, которое максимизирует выигрыши, решающее значение имеет соотношение не самих V и W, a P(S) ∙ V и P(N) ∙ W (они совпадают, только если P(S) = 0, 5). Если P(S) ∙ V = P(N) ∙ W, правило принятия решения должно быть установлено так, чтобы минимизировать вероятности ошибок обоих родов. Если же P(S) ∙ V > P(N) ∙ W, то правило целесообразно изменить так, чтобы сделать возможно меньшей вероятность пропуска, 1-р(Н), даже если при этом увеличивается вероятность ложной тревоги, р(РА).
|
|
|
* Дополнительная информация о критериях оптимальности принимаемого наблюдателем решения приведена в приложении к данной главе.
Возникает вопрос: что ограничивает набор возможных схем соответствия? Почему, в частности, испытуемый не всегда может выработать " правильную" схему соответствия, при которой р(Н) = 1 и p(FA) = 0? Ответ на эти вопросы требует построения формальной модели следующих процессов: 1) какое соответствие существует между предъявлениями < S> и < N> и их сенсорными репрезентациями; 2) как по данной сенсорной репрезентации строится ответ (" Да" или " Нет" ). Мы изложим здесь одну из простейших моделей, отвечающих на эти вопросы.
Суть модели состоит в следующем. Любой стимул (< S> или < N> ) связан с его сенсорными репрезентациями стохастически (т. е. вероятностно, случайно), а не детерминистически. Это означает, что один и тот же стимул, повторяясь в различных пробах, вызывает различные сенсорные образы, так что в каждой отдельной пробе можно говорить только о вероятностях возникновения тех или иных сенсорных образов. Причины такой стохастичности многочисленны. С одной стороны, они могут лежать в природе самого стимула (например, количество квантов, излучаемых источником света в данном направлении в единицу времени — величина принципиально стохастическая) и в ограниченной точности приборных измерений. С другой стороны, стохастичность связана со случайными флуктуациями в сенсорной системе, например, со спонтанной нервной активностью в проводящих путях. Последняя, в частности, обеспечивает наличие различных сенсорных образов и в том случае, если пустой стимул < N> представляет собой отсутствие энергии в данной пространственно-временной области. Кроме того, известный вклад в стохастичность сенсорных эффектов безусловно вносят и так называемые внешние факторы: нестабильность стимуляционной аппаратуры, различного рода помехи и т. д.
|
|
|
Далее в излагаемой модели предполагается, что установленное правило соответствия имеет детерминистическую структуру, т. е. данный сенсорный образ, если он в точности повторился в двух пробах (причем за время между пробами схема соответствия не изменилась), вызовет всегда один и тот же ответ. Другими словами, любое правило принятия решения однозначно разбивает множество всех возможных ощущений на два класса — один, связанный с ответом " Да", другой — с ответом " Нет". На рис. 1 точками заполнены те области, которые связаны с ответом " Да". На рис. 2 области с горизонтальной (вертикальной) штриховкой соответствуют ощущениям, которые могут быть вызваны стимулами < S> и < N>.
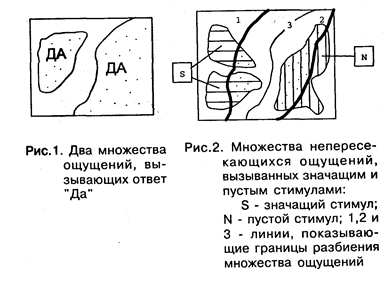
Линии 1, 2 и 3 показывают границы разбиения, соответствующего трем схемам соответствия, причем область " Да" при всех схемах соответствия лежит слева от этих границ. Рассмотрим сначала схему соответствия 1. Мы видим, что при такой схеме < N> всегда будет идентифицироваться правильно, т. е. p(FA) = 0. Однако, < S> иногда (когда ощущение, вызванное < S>, попадает правее границы — эта область помечена точками) вызовет ответ " Нет", т. е. испытуемый будет иногда пропускать сигнал, р(Н) < 1. При схеме соответствия 2 ситуация обратна. Испытуемый всегда идентифицирует < S> как " Да", т. е. р(Н) = 1, но иногда (эта область помечена точками) < N> будет вызывать ответ " Да" (ложная тревога), т. е. p(FA) > 0. Легко видеть, однако, что при данном сорасположении ощущений, вызываемых < S> и < N>, испытуемый может в принципе выработать такую схему соответствия (граница 3, штриховая линия), при которой можно избежать ошибок, т. е. p(FA) = 0 и р(Н) = 1. Причина, обеспечивающая эту возможность, заключается в том, что указанные области не пересекаются, т. е. нет ни одного ощущения, которое могло бы быть вызвано (пусть с разной вероятностью) как < S>, так и < N>. Если это условие не выполняется (см. рис. 3), то, очевидно, при любой схеме соответствия испытуемый будет совершать ошибки того или иного рода (О или FA), либо и те, и другие.
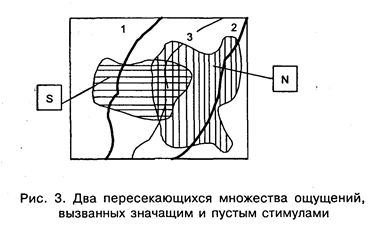
Такова суть модели. Чтобы представить модель в количественной форме, допускаются два дополнительных упрощения. Первое из них может быть разъяснено следующим образом. Схема соответствия с содержательной точки зрения представляет собой соответствие данного ответа некоторому комплексу свойств сенсорного образа: " Если образ обладает свойствами таким-то и таким-то, то следует выбрать ответ " Да", в противном случае — " Нет". Очевидно, что не все свойства образа при этом используются. Рассматриваемое упрощение состоит в предположении, что решение принимается всегда на основе интенсивности какого-то одного качества сенсорных образов (" сладкость", " наклонность", " яркость" и т. п. ), причем правило принятия решения имеет форму: " Если интенсивность (выраженность) качества больше некоторой величины С, то следует выбрать " Да", в противном случае — " Нет". Интенсивность качества, как это видно из предыдущей фразы, предполагается представимой действительным числом. Таким образом все возможные значения интенсивности данного качества занимают какую-то часть оси действительных чисел (например, всю положительную полуось), причем каждое из этих значений при предъявлении данного стимула может быть вызвано с тем или иным правдоподобием. Если значения интенсивности сенсорных образов образуют непрерывный континуум, то это правдоподобие выражается не вероятностью, а плотностью вероятности. Плотность вероятности возникновения ощущения со значением интенсивности ощущения Х при подаче стимула А условимся обозначать через f (X/A).
|
|
|
Вернемся теперь к нашей ситуации, где стимул есть либо < S>, либо < N>. Каждому из стимулов соответствует своя функция плотности вероятности: f (X/S) и f (X/N) (рис. 4).
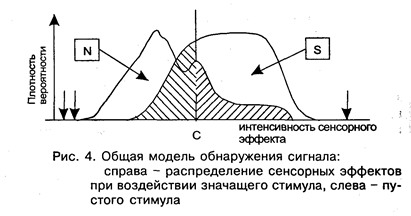
Согласно принятому утверждению, правило принятия решения определяется выбором граничной точки С (ее еще называют критической точкой или величиной критерия принятия решения о наличии сигнала), такой, что если интенсивность Х в данной пробе превышает С, то следует ответ " Да", если же не превышает, то — " Нет". Легко видеть по рисунку, что вероятность ложной тревоги p(FA) равна вероятности того, что интенсивность Х (при условии, что предъявлен < N> ) превзойдет С, т. е. равна заштрихованной области под кривой f (X/N). Вероятность попадания р(Н) равна вероятности того, что Х (при условии, что предъявлен < S> ) превзойдет С, т. е. равна незаштрихованной области под кривой f (X/S).

Если критерий С находится далеко вправо (показано на рис. 4 одной стрелкой), то, очевидно, p(FA) = p(H) = 0. Если теперь начать двигать критерий справа налево, то при каждом очередном значении мы будем получать новую пару p(FA) и р(Н), причем оба значения будут возрастать (или по крайней мере не убывать), пока при достаточно далеком левом положении С оба не станут равны 1 (показано двумя стрелками на рис. 4). Поскольку каждое значение С однозначно определяет пару чисел p(FA) и р(Н), то ему можно поставить в соответствие точку внутри квадрата (рис. 5), на вертикальной стороне которого откладывается р(Н), а на горизонтальной — p(FA), и таким образом представить результат работы наблюдателя.

Полученная по этим точкам кривая называется рабочей характеристикой наблюдателя или просто — РХ. Любая пара распределений, f (X/S) и f (X/N) однозначно определяет РХ, но обратное неверно: одна и та же РХ может определяться различными парами f (X/S) и f (X/N). РХ идет из точки (0, 0) квадрата в точку (1, 1) и при этом располагается выше его главной диагонали. Последнее следует из того, что распределение f (X/S) сдвинуто вправо этносительно f (X/N), т. е. р(Н) превышает p(FA)*.
* Очевидно, что когда наблюдатель фактически не обнаруживает сигнал и p(H) = p(FA), точки РХ будут лежать на диагонали.
Вероятности р(Н) и p(FA) меняются содружественно, т. е. нельзя только путем изменения схемы соответствия одновременно увеличить одну из них и уменьшить другую (или, что то же самое, нельзя одновременно уменьшить или увеличить вероятности ошибок обоих родов, FA и О). Это очень важное положение верно для любых пар f (X/S) и f (X/N). Из него следует, что только пара этих вероятностей, а не каждая в отдельности, характеризует сенсорную способность наблюдателя.
Допустим, в эксперименте с симметричной платежной матрицей (V=W) и P(S) = 0, 5) испытуемый установил положение критерия, как это показано на рис. 6а.

Результаты этого мысленного эксперимента с так называемым симметричным критерием представлены в таблице 3.
Таблица 2
|
|
|


